ポアソン分布を導出する

ポアソン分布という確率分布を習ったのでまとめてみます。ポアソン分布は二項分布と近い関係があります。具体的には、回数が大きく、発生確率が少ない時二項分布の近似とみなせます。まずは二項分布から見ていきます。

二項分布

二項分布は発生確率pの事象Aがあったとして、それがn回の試行で何回起こるか?を表したもの。n回の試行でk回起こる確率は

nとpで形が決まる分布になっていることを確認してください。

ポアソン分布

二項分布の期待値λは事象Aの発生確率pに回数nをかけたものです。例えば、100回コインを投げて表が出る期待値は100*0.5=50（回）となります。つまり、期待値λはλ=npとなります。二項分布はnとpをパラメタに置く関数でしたが、ポアソン分布はλだけで二項分布を表現し、nを非常に大きく、pを非常に小さくという縛りを加えることで近似できるようにしたものです。

ポアソン分布は二項分布（及びその近似としてよく使われる正規分布）と比べると計算が少なく楽なので、可能であればポアソン分布を使いたいケースが多いようです。

天下り的ですが、ポアソン分布の式は↑です。二項分布を、ポアソン分布の式を目がけてガシガシ変形します。

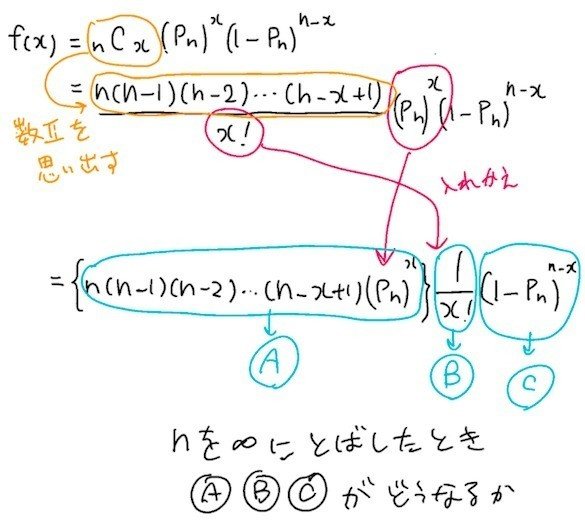
高校の頃ならったcombinationを思い出しつつゴニョゴニョいじり、二項分布の式をA,B,Cの3パートに分割します↑。nが非常に大きい、つまりn→∞という縛りがありましたが、Bはnが含まれていないのでどんなnでも不変ゆえ無視できます。なので、AとCだけ考えます。

Aは↑のようにして求めます。nをx個分子に配り、同じ数を分母に置いて相殺し、等号がなりたつようにします。テクニカルですね〜。つぎに、各項を(1-k/n)の形に変形し、nを無限大に飛ばして1に近づけるのですが、nが充分おおきくないと、この導出自体があやしくなるので正しい近似にならないことがわかると思います。

Cは極限を使った自然対数の定義を道具に使うので事前に知っておく必要があります。

これで、ポアソン分布の確率関数が求まりました。テクニカルですが極限の復習になりました。次回は実データを使ってポアソン分布の威力を実証してみることにします。