新しいUEFAチャンピオンズリーグのリーグ戦形式を考えてみる
UEFAチャンピオンズリーグ 新形式を発表
UEFAが新しいチャンピオンズリーグの大会形式を発表しました.
⚽ The #UEFAExCo has approved the final format and access list for UEFA club competitions from the 2024/25 season.
— UEFA (@UEFA) May 10, 2022
✅ No more access granted based on club coefficients.
✅ Eight matches instead of ten in the new league phase.
Full details: ⬇️#UCL #UEL #UECL
要約:
参加チーム数は32から36に変更
単一のリーグで各チーム少なくとも8試合(ホームアウェーそれぞれ4試合)を行う.それぞれの対戦相手は異なる.
上位8チームは決勝トーナメント進出.9位から24位がプレイオフを争う.
上記の条件で,なるべく公平な形式を考えてみました.「なるべく」なので証明の類はありません.
基本の発想
36チームで各8試合なので,4チーム×9グループ(便宜的にG1からG9)に分け,他のグループとのみ対戦することにしよう.
36チームは何らかの実力順で並んでいるものとし,他のグループ内の1位から4位とそれぞれ2試合ずつ均等に対戦することとしたい.
この条件で,各グループとグループ間の対戦の種類を均等にしてみたのがこちらです.
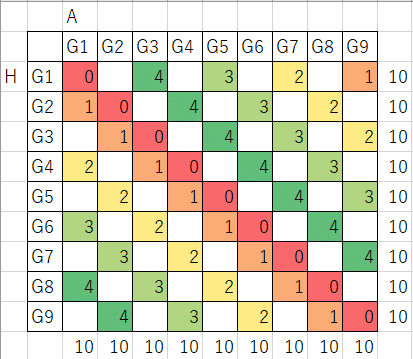
縦横軸はそれぞれホーム・アウェーチームのグループ名,数字は対戦パターン4種類です.たとえば,G2の4チームはホームでG1, G4, G6, G8からそれぞれ1チーム,アウェーでG3, G5, G7, G9からそれぞれ1チームと合計8試合対戦します.
縦横それぞれパターンが均等になっている(どの行・列も1から4が1回ずつ現れている)ことがわかります.
次にそれぞれの対戦パターンをどうするか?ですが,2通り作成してみました.細かいですが両方とも図示します.


対戦を図示したとき,左下斜め(パターン1)と右下斜め(パターン2)の2通りを作りました.これで条件の2個目(「他のグループ内の1位から4位とそれぞれ2試合ずつ均等に対戦する」)は満たせているはずです.
均一性などをどう評価しよう?
どちらの対戦表がいいのだろうか?を考えるために,グラフとして図示してみます.対戦チーム間に辺がある無向グラフとしてみます.


何となくパターン1の方がチーム間が近くなるように密集していて,パターン2には遠い組み合わせがあるように見えます.
すべての組み合わせに対する距離を計算してみます.自分自身との距離は0,直接対戦がある組み合わせは距離1,対戦相手の対戦相手は距離2,…と定義します.
すべての組み合わせに対する距離を集計しました.プログラムをさぼったので始点と終点を区別してしまっています(36^2=1296通り).


グラフの図示からの直感通り,パターン1の方がチーム間の距離が近いことがわかりました.
不均一で総当たりでないリーグ戦では,対戦のないチーム間の実力差は対戦結果をつなげることで推測されます.
例:実力差が得失点差に直接現れると仮定し,試合結果がA 2-1 B,B 1-3 Cとします.AとCが対戦していない場合,もし対戦したとしたらCが1点分Aより強い,と考えます(Masseyのレーティング).
この仮定の下ではチーム間の距離は平均的に小さいことが望ましいので,パターン1の方がよさそう,ということになります.
ひとまずの結論
「パターン1」の対戦表がよさそう.
これより良いものがあるかどうかは調べていません.