見出し画像

Jリーグは失点の何倍得点すれば優勝できる/降格しないリーグなのでしょうか？

konakalab

記事の概要

・Jリーグ(J1リーグ)の優勝や降格と，得失点の関係を集計しました．

・得失点比で2.0倍，1.5倍がそれぞれ優勝濃厚・優勝争いの分かれ目になりそうです．降格についても似た感じです．

まえおき

Jリーグでは優勝争いと残留争いが大きな関心事なわけですが，その目安として「平均勝ち点2(勝ち点68)」「平均勝ち点1(勝ち点34)」が分かりやすいのではないか？というツイートがありまして，なるほどな，と思いました．これは格言として覚えやすくてよいです．

実際に過去15年程度を集計してみると，この「格言」は実情をよく表しているようです．以下に図を示します．2020年は11/10時点のデータで，2015年，2016年の順位は年間総勝ち点に基づくものです．

画像1

優勝争いはこちら．平均勝ち点2.0を超えれば確実に優勝争いをしています．2.0以下でも優勝はぽつぽつあります．

画像2

残留争いはこちら．16位から18位が降格に関わる(16位は年により自動降格かプレーオフかが異なる)のですが，平均勝ち点1.0=勝ち点34はまさに16位の当落線上，という趣です．

得失点についても調べてみる

これを，得失点についても調べてみます．順位表に乗るのは得失点差ですが，ここでは得失点比=得点/失点を利用します．理由はちょっと技術的になるので割愛します．直感的には「1失点する間に何点取れるか？」がすべての球技での本質であろう，という立場です．

画像3

横軸は得点(GoalsFor)/失点(GoalsAgainst)(対数軸にしています)，縦軸は平均勝ち点．順位はマーカと色で区別しています．この図からわかることは以下でしょうか．

・失点の2倍得点できればほぼ優勝(実例ではすべて優勝)．

・失点の1.5倍得点できれば優勝争い．

・得点の1.5倍失点してしまうと残留争い．

・得点の2倍失点してしまうとほぼ降格(実例ではすべて16位から18位)．

余談：ポアソン分布でシミュレーションしてみる

平均得失点からポアソン分布を利用して勝敗の予測確率を求めることができます．

総得失点の3パターン(少ない：65，平均：92，多い：115)それぞれについて，得失点比から平均得失点を算出し，それに基づいて34試合をポアソン分布を利用してシミュレーションしたときの勝ち点の分布(平均±2標準偏差)を示します．

画像4

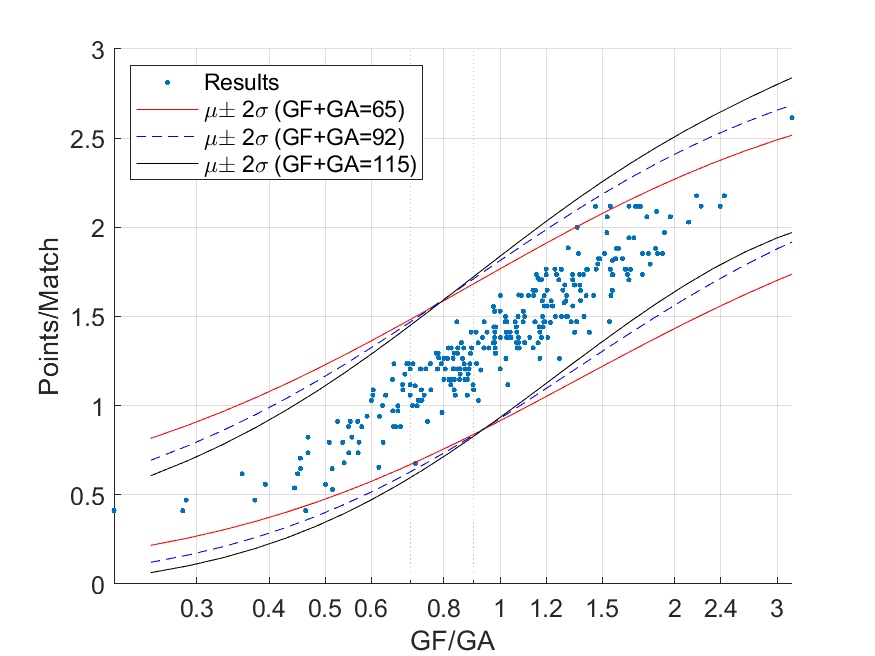
青点が実際の結果で，線が上下限を示しています．総得失点が少ないほど引き分けが増えるので勝ち点の変化が緩やかになります．ポアソン分布でのシミュレーションはそこまで的外れではないのかな，と思われます．

得失点比が1.0，つまり平均得失点が等しい場合の平均勝ち点の平均-2標準偏差は0.8くらいで，ごくまれに得失点が同等でも降格争いに加わるチームがありそう，という予測になります(実際，得点が失点より多いのに降格してしまったチームは過去1チームあります)．したがって，降格対象の3チームの中には「失点と同じくらい得点できるのに，運やめぐりあわせが悪すぎて平均勝ち点が1.0を下回ってしまった」チームはほとんど含まれていないことになります．言い換えると，運以外にも得点が失点を下回ってしまうような何かがあるチームが降格対象になっていることが分かります．実力はあるが運が伴っていないだけのチームを降格させるのは悪影響でしょうから，「18チーム中3チームが降格対象」というのはいいバランスなんだなー，とわかります．

そういえば，似たような記事を前に書いていました．ネタがかぶってますね．

「降格チーム数は，確実に実力に差があるとわかるチーム数のみを対象としたい」という基準であるべきともし仮定するのであれば，異例の20チームで構成される2021年のJ1で，何チームが降格対象になるのか？が気になってきますね．過去の統計も利用できないので難しい判断になりそうです．


いいなと思ったら応援しよう！