線形回帰モデル

・回帰問題：ある入力x(離散あるいは連続値)から出力y(連続値)を予測する問題

・回帰での入力と出力：x=(x1~xn)∊Rn , y∊R1

・線形回帰モデル：`y = w.T ・ x + w0 (  w=(w1~xm)∊Rm  )

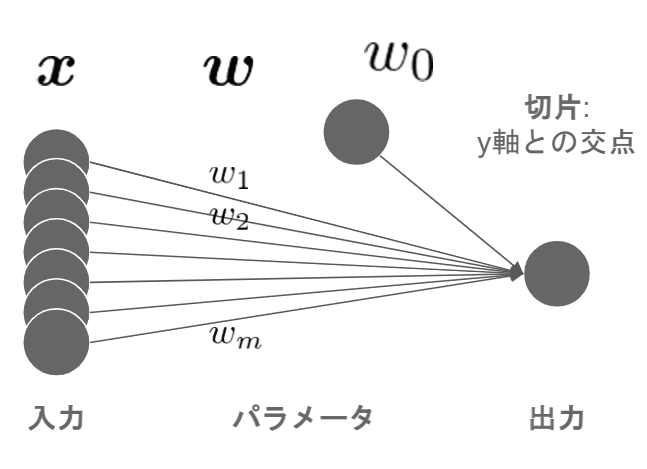
・説明変数ｘが1次元の場合(n,m=1、単回帰)：`y = w0 +w1x1 + b

・説明変数ｘが多次元の場合(n,m>1、重回帰)：`y = w.T ・ x + b

課題：(ボストンの住宅データセット)部屋数が4で犯罪率が0.3の物件はいくらになるか？→ 4.2401千ドル

python実装：

from sklearn import linear_model
import numpy as np

x = np.arange(20).reshape(-1,1)
y = np.asarray([20055.80,20032.35,20081.63,19994.06,19929.09,20080.98,20195.48,20098.38,20099.81,20118.86,19999.91,20020.86,20144.59,20099.75,19975.67,19955.20,20050.16,20079.64,19959.84,19925.18])

clf = linear_model.LinearRegression()
clf.fit(x, y)

import matplotlib.pyplot as plt
plt.scatter(x, y)
plt.plot(x, clf.predict(x))

#以下からは課題の解
from sklearn.datasets import load_boston
boston = load_boston()
x = boston.data[:,[0,5]]#0番目が犯罪率、5番目が部屋数
y = boston.target

clf = linear_model.LinearRegression()
clf.fit(x, y)
res = clf.predict([[0.3,4]]) #  4.24007956

考察：

・線形回帰モデルは実質上一方程式のフィッティング問題に相当する

・線形回帰モデルは単層ニューラルネットワークに相当する

・線形回帰におけるｗとbを求めるには最小自乗法などが良く使われる

・最適化に関しては最小二乗法以外に遺伝的アルゴリズムも求められる