
多変量ガウス分布の仕組みをキモチで理解する。
統計学の授業で正規分布を勉強した人は多いと思います。正規分布に従う変数が$${n}$$個ある時にその$${n}$$個の変数が全体としてどのように分布するのか、を表したのがが多次元ガウス分布です。(正規分布はしばしばガウス分布とも呼ばれます。)
ネットで「多変量ガウス分布」と検索すると数学的な理解に重きを置いた記事ばかりがヒットしてきたのでできる限り多変量ガウス分布の仕組みを目で見て気持ちで理解するような記事にしたつもりです。Rを使って使って多変量ガウス分布の部分的な情報を取り出して可視化していくプロセスについても書いてみました。
1変数のガウス分布(知ってたら飛ばしてください)
$$
\Nu(x|\mu, \sigma^2) = \frac{1}{\sqrt{2\pi} \sigma} e^{(- \frac{(x - \mu)^2}{2\sigma^2})}
$$
ガウス分布は平均$${\mu}$$と分散$${\sigma^2}$$によって定義されます。また先頭の$${\frac{1}{\sqrt{2\pi}\sigma}}$$はただの定数(積分した時に面積が1になるように調整するだけの役割)なので関数本体は$${e^{(- \frac{(x - \mu)^2}{2\sigma^2})}}$$で決まります。また、平均$${\mu}$$は分布を平行移動させるだけなので、分布自体の形状(即ち広がり具合)は$${\sigma}$$のみに依存します。
ガウス分布からのランダムサンプル

#####正規化されたガウス分布からのランダムサンプル#####
#サンプリング
set.seed(8787)
sample_size <- 10
randG_1 <- rnorm(n = sample_size, mean = 0, sd = 1)
randG_2 <- rnorm(n = sample_size, mean = 3, sd = 2)
#図示
curve(dnorm(x, mean = 0, sd = 1), from = -3, to = 9, col = "red", xlab = "", ylab = "", main = "ガウス分布からの10個のサンプル")
points(x = randG_1, y = numeric(length = sample_size), col = "red")
curve(dnorm(x, mean = 3, sd = 2), add = TRUE, col = "blue")
points(x = randG_2, y = numeric(length = sample_size), col = "blue")赤のグラフ:
平均0、標準偏差1のガウス分布から10個の点をランダムにサンプリングして図にしてみると平均の0を中心に点が集まっていて平均から大きく離れた点は殆どありません。
青のグラフ:
平均3、標準偏差2のガウス分布。標準偏差が赤のグラフより大きいので点の散らばりも大きいです。
多変量ガウス分布の見方
次元が$${D}$$の確率密度関数は
$$
\Nu(\bm{x}|\bm{\mu}, \bm{\Sigma}) = \frac{1}{(\sqrt{2\pi})^D \sqrt{|{\bm{\Sigma}|}}} e^{(
-\frac{1}{2} (\bm{x} - \bm{\mu})^T \Sigma ^{-1} (\bm{x} - \bm{\mu})
)}
$$
と表されます。$${\bm{\mu} = (\mu_1, \mu_2, …, \mu_D)}$$は$${x}$$の期待値をあらわす平均ベクトル、$${\bm{\Sigma}}$$はその$${(i,j)}$$要素が$${x_i}$$と$${x_j}$$の共分散を表す$${D×D}$$行列、共分散行列です。
簡単な例として、最初は二次元の場合で考えます。
ガウス分布を2次元に拡張
上にも書いた通り、多変量ガウス分布の形は共分散行列$${\bm{\Sigma}}$$で定まります。$${\bm{\Sigma}}$$が$${2×2}$$行列のとき、$${(1,1)}$$要素と$${(2,2)}$$要素は自分自身との共分散、つまりそれぞれ$${x_1}$$と$${x_2}$$の分散を表しています。そして$$(1,2)$$要素、$${(2,1)}$$要素はどちらも$${x_1}$$と$${x_2}$$の共分散を表しています。
共分散行列の意味
$$
\begin{bmatrix}1 & 0.9\\0.9 & 1\\\end{bmatrix}
\begin{bmatrix}1 & 0.3\\0.3 & 1\\\end{bmatrix}
$$
まずは、上の2つの共分散行列を成す$${(x_1, x_2)}$$のランダムサンプルを散布図にしてみたいと思います。($${x_1}$$、$${x_2}$$は両方とも平均0に設定したのでどちらの変数も標準正規分布に従います。何故ならどちらの共分散行列も$${(1, 1)}$$要素と$${(2, 2)}$$要素は1なので$${x_1}$$も$${x_2}$$も標準偏差は1だからですね。)

#共分散行列の定義
library(MASS)
sigma1 <- matrix(c(1, 0.9, 0.9, 1), ncol = 2)
sigma2 <- matrix(c(1, 0.3, 0.3, 1), ncol = 2)
#サンプル
set.seed(8787)
sample_size2 <- 100
sample_meanvector <- c(0, 0)
rand2G_1 <- MASS::mvrnorm(n = sample_size2, mu = sample_meanvector, Sigma = sigma1)
rand2G_2 <- MASS::mvrnorm(n = sample_size2, mu = sample_meanvector, Sigma = sigma2)
#図示
par(mfrow = c(1, 2))
plot(rand2G_1, xlab = 'x1', ylab = 'x2', main = '共分散0.9')
plot(rand2G_2, xlab = 'x1', ylab = 'x2', main = '共分散0.3')共分散0.9のグラフは、共分散0.3のグラフに比べて、斜めの方向にまとまりのある分布をしているように見えます。何故なら、共分散が大きいという事は、2つの変数の値の取り方が似ているということを意味しているからです。2次元の場合は、共分散が大きいということは$${x_2 = x_1}$$の直線付近に集まるような挙動が確認できるということです。
これらの2つの共分散行列から成るガウス分布をプロットすると。。。

#多変量正規分布の密度関数のためのライブラリ
library(mvtnorm)
#平面の二本の軸を作成
x1 = seq(-3, 3, length = 50)
x2 = x1
#共分散行列に応じた確率密度関数の指定
f1 = function(x1, x2) {
dmvnorm(matrix(c(x1, x2), ncol = 2), mean = mean_vector, sigma = sigma1)
}
f2 = function(x1, x2) {
dmvnorm(matrix(c(x1, x2), ncol = 2), mean = mean_vector, sigma = sigma2)
}
#あらゆる(x1, x2)の組(50×50)の組を作ってf1とf2に放り込む
#ある意味上のスキャッタープロットを作成して、各点をf1とf2という関数に入力する作業がこれ。
z1 = outer(x1, x2, f1) #outer関数は、あらゆる(x1, x2)の組を作ってf1に放り込むようなことができる。
z2 = outer(x1, x2, f2) #そのままf1(x1, x2)とすると(x1_1, x2_1),,,(x1_50. x2_50)の同じサブスクリプトの組しか作り事ができない。
#3次元をプロットするpersp関数を使う。
par(mfrow = c(1,2))
persp(x1, x2, z1, theta=-30, phi=35, col = 'skyblue') #thta で横向きの回転の角度を指定
persp(x1, x2, z2, theta=-30, phi=35, col = 'skyblue') #phi で縦向きの回転の角度を指定左の図がが共分散0.9,右の図がが共分散0.3です。共分散が大きいと、つまり二つの変数が似たような値を取る時、分布の形は鶏のトサカのように平べったい形になりますね。似たような値を取るとおうことは$${x_2 = x_1}$$の直線(というか平面)の付近に点が集まりやすいということですから。共分散が一方で、小さく$${x_1}$$と$${x_2}$$の間に関係があまりない時、分布は綺麗な山のような形に近づいていきます。
次に、3次元以上に拡張していく前準備として$${D>2}$$のときの$${D×D}$$の共分散行列についてみていきます。
D次元への拡張とカーネル
これ以上は目で全体像を見ることはできません。なので一部分の情報を取り出して頑張って全体の形を感じるという方法で全体像を確認していきます。
カーネル
$${x_1,…, x_D}$$の関係性(値の近さ)を表す共分散行列ですが、$${x_1,…, x_D}$$からすべての共分散を求めて全体像を調べるよりも、先に共分散行列を定義してしまうことがよくあります。例えば無限個の$${x}$$を全て書き下すことなく扱えることや、機械学習の場面で条件によっては入力ベクトルとしての$${x}$$を明示的に表す必要性が無くなることもあってこの方法が使われます。
各要素は結局$${(x_i, x_j)}$$の関数として捉えることができるので各$${(x_i, x_j)}$$を入力とした関数$${K_{ij}}$$を作り、その出力を共分散行列の$${(i,j)}$$要素とするわけです。この関数はカーネル関数とよばれており、カーネル関数から計算される共分散行列をカーネル行列と言います。カーネル関数には様々なあるのですが、いくつかの種類のカーネル関数からカーネル行列を作ってそれで定義されるガウス分布を比較してみようと思います。
RBFカーネル(動径基底関数カーネル)
$$
k(x_i, x_j) = \theta_1 e^{(
- \frac{|x_i - x_j|^2}{\theta_2}
)}
$$
この関数でRBFカーネルが定義されます。$${\theta_1}$$と$${\theta_2}$$でこのカーネル関数の性質がきまるのですが、今回の本題からはそれるので適当に$${\theta_1 = \theta_2 = 1}$$として進めます。(機械学習の場面ではこの$${\theta}$$がハイパーパラメータとしてチューニングされます。)ちなみに、$${x_i}$$と$${x_j}$$の値が遠い時、$${ e^{(- \frac{|x_i - x_j|^2}{\theta_2})}}$$が小さくなり$${x_i}$$と$${x_j}$$が近い時$${ e^{(- \frac{|x_i - x_j|^2}{\theta_2})}}$$が大きくなります。つまり、近い$${x_i}$$と$${x_j}$$の共分散は大きくなり似たような値を取りやすいという傾向がみられます。
線形カーネル
$$
k(x_i, x_j) = x_i^Tx_j
$$
周期カーネル
$$
k(x_i, x_j) = exp(\theta_1 cos(\frac{|x_i - x_j|}{\theta_2}))
$$
これもRBFカーネルと同様に$${\theta_1 = \theta2 = 1}$$として進めます。
#カーネルの定義
#RBFカーネル
theta <- c(1,1)
distance <- function(a,b){ sqrt(sum( (b-a)^2 )) }
RBFkernel <- function(x1, x2, theta){
d <- distance(x1, x2)
theta[1] * exp(-( d**2/theta[2] ))
}
#線形カーネル
LinearKernel <- function(x1, x2){t(x1)%*%x2}
#周期カーネル
theta <- c(1,1)
PeriodicKernel <- function(x1, x2){
exp(theta[1]*cos(abs(x1-x2)/theta[2]))
}カーネル行列を得る
#カーネル行列の計算
dimension <- 100
mean <- rep(0, dimension)
x <- seq(-5, 8, length.out = 100)
#RBFカーネル
CovMatrix_RBF <- matrix(0, dimension, dimension) #空っぽの行列。以下、これを埋める
for (i in 1:length(x)) {
for (j in 1:length(x)) {
CovMatrix_RBF[i, j] <- RBFkernel(x[i], x[j], theta)
}
}
#線形カーネル
CovMatrix_Linear <- matrix(0, dimension, dimension)
for (i in 1:length(x)) {
for (j in 1:length(x)) {
CovMatrix_Linear[i, j] <- LinearKernel(x[i], x[j])
}
}
#周期カーネル
CovMatrix_Periodic <- matrix(0, dimension, dimension)
for (i in 1:length(x)){
for (i in 1:length(x)){
CovMatrix_Periodic[i, j] <- PeriodicKernel(x[i], x[j], theta)
CovMatrix_Periodic[j, i] <- CovMatrix_Periodic[i, j]
}
}分布からのサンプリング
2次元に時のように全体像は確認できませんが、今までのようにサンプルを取って可視化することで分布の挙動を確認することはできます。ということで、2次元の時に使ったmvtnormライブラリのrmvnorm関数を使ってサンプリングをしていきます。コードは以下です
#サンプリング
n = 5
#RBF
RBFsample <- mvtnorm::rmvnorm(n, mean, CovMatrix_RBF)
#線形
LinearSample <- mvtnorm::rmvnorm(n, mean, CovMatrix_Linear)
#周期
PeriodicSample <- mvtnorm::rmvnorm(n, mean, CovMatrix_Periodic)サンプルを可視化する。


#図示
RBFsample <- data.frame(t(RBFsample))
LinearSample <- data.frame(t(LinearSample))
PeriodicSample <- data.frame(t(PeriodicSample))
color <- c('red', 'blue', 'green', 'black', 'orange')
shape <- c(0, 2, 4, 6, 8)
# RBF
ggplot() +
geom_point(aes(x = x, y = RBFsample[, 1]), color = color[1], alpha = 0.6, shape = shape[1])+
geom_line(aes(x = x, y = RBFsample[, 1]), color = color[1], alpha = 0.6) +
geom_point(aes(x = x, y = RBFsample[, 2]), color = color[2], alpha = 0.6, shape = shape[2])+
geom_line(aes(x = x, y = RBFsample[, 2]), color = color[2], alpha = 0.6) +
geom_point(aes(x = x, y = RBFsample[, 3]), color = color[3], alpha = 0.6, shape = shape[3])+
geom_line(aes(x = x, y = RBFsample[, 3]), color = color[3], alpha = 0.6) +
geom_point(aes(x = x, y = RBFsample[, 4]), color = color[4], alpha = 0.6, shape = shape[4])+
geom_line(aes(x = x, y = RBFsample[, 4]), color = color[4], alpha = 0.6) +
geom_point(aes(x = x, y = RBFsample[, 5]), color = color[5], alpha = 0.6, shape = shape[5])+
geom_line(aes(x = x, y = RBFsample[, 5]), color = color[5], alpha = 0.6) +
theme_minimal() +
xlab('') + ylab('') + ggtitle('RBFカーネル')
#線形
ggplot()+
geom_point(aes(x = x, y = LinearSample[, 1]), color = color[1], alpha = 0.6, shape = shape[1])+
geom_line(aes(x = x, y = LinearSample[, 1]), color = color[1], alpha = 0.6)+
geom_point(aes(x = x, y = LinearSample[, 2]), color = color[2], alpha = 0.6, shape = shape[2])+
geom_line(aes(x = x, y = LinearSample[, 2]), color = color[2], alpha = 0.6)+
geom_point(aes(x = x, y = LinearSample[, 3]), color = color[3], alpha = 0.6, shape = shape[3])+
geom_line(aes(x = x, y = LinearSample[, 3]), color = color[3], alpha = 0.6)+
geom_point(aes(x = x, y = LinearSample[, 4]), color = color[4], alpha = 0.6, shape = shape[4])+
geom_line(aes(x = x, y = LinearSample[, 4]), color = color[4], alpha = 0.6)+
geom_point(aes(x = x, y = LinearSample[, 5]), color = color[5], alpha = 0.6, shape = shape[5])+
geom_line(aes(x = x, y = LinearSample[, 5]), color = color[5], alpha = 0.6)+
theme_minimal()+
xlab('')+ylab('')+ggtitle('線形カーネル')
#周期
ggplot()+
geom_point(aes(x = x, y = PeriodicSample[, 1]), color = color[1], alpha = 0.6, shape = shape[1])+
geom_line(aes(x = x, y = PeriodicSample[, 1]), color = color[1], alpha = 0.6)+
geom_point(aes(x = x, y = PeriodicSample[, 2]), color = color[2], alpha = 0.6, shape = shape[2])+
geom_line(aes(x = x, y = PeriodicSample[, 2]), color = color[2], alpha = 0.6)+
geom_point(aes(x = x, y = PeriodicSample[, 3]),color = color[3], alpha = 0.6, shape = shape[3])+
geom_line(aes(x = x, y = PeriodicSample[, 3]), color = color[3], alpha = 0.6)+
geom_point(aes(x = x, y = PeriodicSample[, 4]), color = color[4], alpha = 0.6, shape = shape[4])+
geom_line(aes(x = x, y = PeriodicSample[, 4]), color = color[4], alpha = 0.6)+
geom_point(aes(x = x, y = PeriodicSample[, 5]), color = color[5], alpha = 0.6, shape = shape[5])+
geom_line(aes(x = x, y = PeriodicSample[, 5]), color = color[5], alpha = 0.6)+
theme_minimal()+
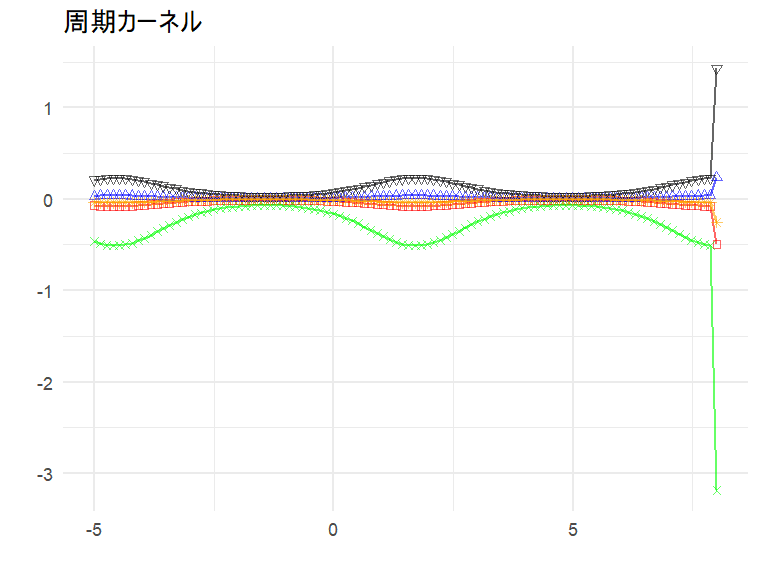
xlab('')+ylab('')+ggtitle('周期カーネル')サンプルの可視化グラフの読み取り方
上の3つのグラフが変数100のガウス分布からの5つサンプリングを可視化したものになります。つまり、1つ1つの線が1つのサンプルを表しています。100個の変数から成るガウス分布から1つのサンプルを取るということは即ち$${(x_1, x_2, …, x_100)}$$を得ることです。なのでこのグラフの線上の点は全部で100個で、またその点たちは$${(x_1, x_2, …, x_100)}$$の順番に並んでいます。
これとカーネル行列(カーネル関数)の関係性に触れておくと、カーネル行列は隣り合う$${x_i}$$と$${x_j}$$$${(i ≠j)}$$の近さの関係性を指定するものと捉えることができます。例えば線形カーネルが最も分かりやすいですが、$${x}$$のサブスクリプトが1増える度に一定の間隔でその値も増える・減るを繰り返します。周期カーネルは周期的に増減を繰り返すパターンを作ります。また、RBFカーネルは特徴的な法則性はありませんが、近い$${x_i}$$と$${x_j}$$は共分散が大きくなり似たような値を取ることからら、ランダムに上下する線グラフにはならず、サンプルの曲線は滑らかな曲線を描きます。また、勿論今回は$${x_i (i = 1,2,…,100)}$$が標準正規分布の従うこともあり、殆どの$${x_i(i = 1, 2, …,100)}$$は$${0}$$を中心に$${-2}$$から$${2}$$の間に集まっています。
コードアペンディクス
#####1次元のガウス分布からのランダムサンプル#####
#サンプリング
set.seed(8787)
sample_size <- 10
randG_1 <- rnorm(n = sample_size, mean = 0, sd = 1)
randG_2 <- rnorm(n = sample_size, mean = 3, sd = 2)
#図示
curve(dnorm(x, mean = 0, sd = 1), from = -3, to = 9, col = "red", xlab = "", ylab = "", main = "ガウス分布からの10個のサンプル")
points(x = randG_1, y = numeric(length = sample_size), col = "red")
curve(dnorm(x, mean = 3, sd = 2), add = TRUE, col = "blue")
points(x = randG_2, y = numeric(length = sample_size), col = "blue")
##### 2次元のガウス分布 #####
#共分散行列の視覚的な確認 #共分散行列の定義
library(MASS)
sigma1 <- matrix(c(1, 0.9, 0.9, 1), ncol = 2)
sigma2 <- matrix(c(1, 0.3, 0.3, 1), ncol = 2)
#サンプル
set.seed(8787)
sample_size2 <- 100
mean_vector <- c(0, 0)
rand2G_1 <- MASS::mvrnorm(n = sample_size2, mu = mean_vector, Sigma = sigma1)
rand2G_2 <- MASS::mvrnorm(n = sample_size2, mu = mean_vector, Sigma = sigma2)
#図示
par(mfrow = c(1, 2))
plot(rand2G_1, xlab = 'x1', ylab = 'x2', main = '共分散0.9')
plot(rand2G_2, xlab = 'x1', ylab = 'x2', main = '共分散0.3')
#分布の形 #多変量正規分布の密度関数のためのライブラリ
library(mvtnorm)
#平面の二本の軸を作成
x1 = seq(-3, 3, length = 50)
x2 = x1
#k等分散行列に応じた確率密度関数の指定
f1 = function(x1, x2) {
dmvnorm(matrix(c(x1, x2), ncol = 2), mean = mean_vector, sigma = sigma1)
}
f2 = function(x1, x2) {
dmvnorm(matrix(c(x1, x2), ncol = 2), mean = mean_vector, sigma = sigma2)
}
#あらゆる(x1, x2)の組(50×50)の組を作ってf1とf2に放り込む
z1 = outer(x1, x2, f1) #outer関数は、あらゆる(x1, x2)の組を作ってf1に放り込むようなことができる。
z2 = outer(x1, x2, f2) #そのままf1(x1, x2)とすると(x1_1, x2_1),,,(x1_50. x2_50)の同じサブスクリプトの組しか作り事ができない。
#3次元をプロットするpersp関数を使う。
par(mfrow = c(1,2))
persp(x1, x2, z1, theta=-18, phi=40, col = 'skyblue') #thta で横向きの回転の角度を指定
persp(x1, x2, z2, theta=-30, phi=40, col = 'skyblue') #phi で縦向きの回転の角度を指定
#ヒートマップ
#####D次元とカーネル#####
#カーネルの定義
#RBFカーネル theta <- c(1,1)
distance <- function(a,b){ sqrt(sum( (b-a)^2 )) }
RBFkernel <- function(x1, x2, theta){
d <- distance(x1, x2)
theta[1] * exp(-( d**2/theta[2] ))
}
#線形カーネル LinearKernel <- function(x1, x2){t(x1)%*%x2}
#周期カーネル theta <- c(1,1)
PeriodicKernel <- function(x1, x2, theta){
exp(theta[1]*cos(abs(x1-x2)/theta[2]))
}
#カーネル行列の計算
dimension <- 100
mean <- rep(0, dimension)
x <- seq(-5, 8, length.out = 100)
#RBFカーネル CovMatrix_RBF <- matrix(0, dimension, dimension) #空っぽの行列。以下、これを埋める
for (i in 1:length(x)) {
for (j in 1:length(x)) {
CovMatrix_RBF[i, j] <- RBFkernel(x[i], x[j], theta)
}
}
#線形カーネル CovMatrix_Linear <- matrix(0, dimension, dimension)
for (i in 1:length(x)) {
for (j in 1:length(x)) {
CovMatrix_Linear[i, j] <- LinearKernel(x[i], x[j])
}
}
#周期カーネル CovMatrix_Periodic <- matrix(0, dimension, dimension)
for (i in 1:length(x)){
for (i in 1:length(x)){
CovMatrix_Periodic[i, j] <- PeriodicKernel(x[i], x[j], theta)
CovMatrix_Periodic[j, i] <- CovMatrix_Periodic[i, j]
}
}
#サンプリング
n = 5
#RBF
RBFsample <- mvtnorm::rmvnorm(n, mean, CovMatrix_RBF)
#線形
LinearSample <- mvtnorm::rmvnorm(n, mean, CovMatrix_Linear)
#周期
PeriodicSample <- mvtnorm::rmvnorm(n, mean, CovMatrix_Periodic)
#図示
RBFsample <- data.frame(t(RBFsample))
LinearSample <- data.frame(t(LinearSample))
PeriodicSample <- data.frame(t(PeriodicSample))
color <- c('red', 'blue', 'green', 'black', 'orange')
shape <- c(0, 2, 4, 6, 8)
# RBF
ggplot() +
geom_point(aes(x = x, y = RBFsample[, 1]), color = color[1], alpha = 0.6, shape = shape[1])+
geom_line(aes(x = x, y = RBFsample[, 1]), color = color[1], alpha = 0.6) +
geom_point(aes(x = x, y = RBFsample[, 2]), color = color[2], alpha = 0.6, shape = shape[2])+
geom_line(aes(x = x, y = RBFsample[, 2]), color = color[2], alpha = 0.6) +
geom_point(aes(x = x, y = RBFsample[, 3]), color = color[3], alpha = 0.6, shape = shape[3])+
geom_line(aes(x = x, y = RBFsample[, 3]), color = color[3], alpha = 0.6) +
geom_point(aes(x = x, y = RBFsample[, 4]), color = color[4], alpha = 0.6, shape = shape[4])+
geom_line(aes(x = x, y = RBFsample[, 4]), color = color[4], alpha = 0.6) +
geom_point(aes(x = x, y = RBFsample[, 5]), color = color[5], alpha = 0.6, shape = shape[5])+
geom_line(aes(x = x, y = RBFsample[, 5]), color = color[5], alpha = 0.6) +
theme_minimal() +
xlab('') + ylab('') + ggtitle('RBFカーネル')
#線形
ggplot()+
geom_point(aes(x = x, y = LinearSample[, 1]), color = color[1], alpha = 0.6, shape = shape[1])+
geom_line(aes(x = x, y = LinearSample[, 1]), color = color[1], alpha = 0.6)+
geom_point(aes(x = x, y = LinearSample[, 2]), color = color[2], alpha = 0.6, shape = shape[2])+
geom_line(aes(x = x, y = LinearSample[, 2]), color = color[2], alpha = 0.6)+
geom_point(aes(x = x, y = LinearSample[, 3]), color = color[3], alpha = 0.6, shape = shape[3])+
geom_line(aes(x = x, y = LinearSample[, 3]), color = color[3], alpha = 0.6)+
geom_point(aes(x = x, y = LinearSample[, 4]), color = color[4], alpha = 0.6, shape = shape[4])+
geom_line(aes(x = x, y = LinearSample[, 4]), color = color[4], alpha = 0.6)+
geom_point(aes(x = x, y = LinearSample[, 5]), color = color[5], alpha = 0.6, shape = shape[5])+
geom_line(aes(x = x, y = LinearSample[, 5]), color = color[5], alpha = 0.6)+
theme_minimal()+
xlab('')+ylab('')+ggtitle('線形カーネル')
#周期
ggplot()+
geom_point(aes(x = x, y = PeriodicSample[, 1]), color = color[1], alpha = 0.6, shape = shape[1])+
geom_line(aes(x = x, y = PeriodicSample[, 1]), color = color[1], alpha = 0.6)+
geom_point(aes(x = x, y = PeriodicSample[, 2]), color = color[2], alpha = 0.6, shape = shape[2])+
geom_line(aes(x = x, y = PeriodicSample[, 2]), color = color[2], alpha = 0.6)+
geom_point(aes(x = x, y = PeriodicSample[, 3]),color = color[3], alpha = 0.6, shape = shape[3])+
geom_line(aes(x = x, y = PeriodicSample[, 3]), color = color[3], alpha = 0.6)+
geom_point(aes(x = x, y = PeriodicSample[, 4]), color = color[4], alpha = 0.6, shape = shape[4])+
geom_line(aes(x = x, y = PeriodicSample[, 4]), color = color[4], alpha = 0.6)+
geom_point(aes(x = x, y = PeriodicSample[, 5]), color = color[5], alpha = 0.6, shape = shape[5])+
geom_line(aes(x = x, y = PeriodicSample[, 5]), color = color[5], alpha = 0.6)+
theme_minimal()+
xlab('')+ylab('')+ggtitle('周期カーネル')参考文献
GaussianProcessSummerSchool(https://www.youtube.com/channel/UCQITXIAgtKlUdfBVhAmTRQA)
この記事が気に入ったらサポートをしてみませんか?
