見出し画像

ジェネラティブアート作成時の頭のなか #AltEdu2022 26 日目

@KojiSaito

　本日のお題は「コンピュータに『ありがとう』と思うようなコード」とのこと。

コンピュータに感謝といえば、莫大な計算をこなしてくれる点にある。手作業で計算していたら、一生かかってもできない程の計算を一瞬で行ってくれる。

　というわけで、コンピュータに感謝するコードは、ある程度の計算負荷をかけるプログラムにしようと思う。

かねてより、ノイズ関数の勾配については、どのようなものになるのか興味を持っていた。なので、それを計算するプログラムを書いてみる：

size(500,500)
background(-1)
for i in range(50*50):
    x=i%50*10;y=i/50*10
    u=x*.01;v=y*.01
    b=noise(u,v)
    s=noise(u+.01,v)-b
    t=noise(u,v+.01)-b
    e=x+s*2000;f=y+t*2000
    line(x,y,e,f)

このプログラムでは、微小に値を変動させ、その時の関数値の差を計算している。縦横方向の偏微分を数値的に計算し、それを方向ベクトルとして解釈し、分かりやすくするために大きさを調整して可視化したものである。

　こんな風にノイズ関数というかノイズ曲面の勾配というかベクトル場は構成されているとは…。私個人としてはなかなか興味深い…と思っているのだが、画像としては、正直、魅力に欠けると言わざるを得ない。

であれば、これはベクトル場に他ならないので、この流れに沿って移動する軌跡を描画したらどうだろう？ - などと思いつく。というわけで、さっそくプログラムを修正する：

size(500,500)
background(-1)
for i in range(50*50):
  x=i%50*10;y=i/50*10
  for j in range(100):
    u=x*.01;v=y*.01
    b=noise(u,v)
    s=noise(u+.01,v)-b
    t=noise(u,v+.01)-b
    e=x+s*2000;f=y+t*2000
    line(x,y,e,f)
    x,y=e,f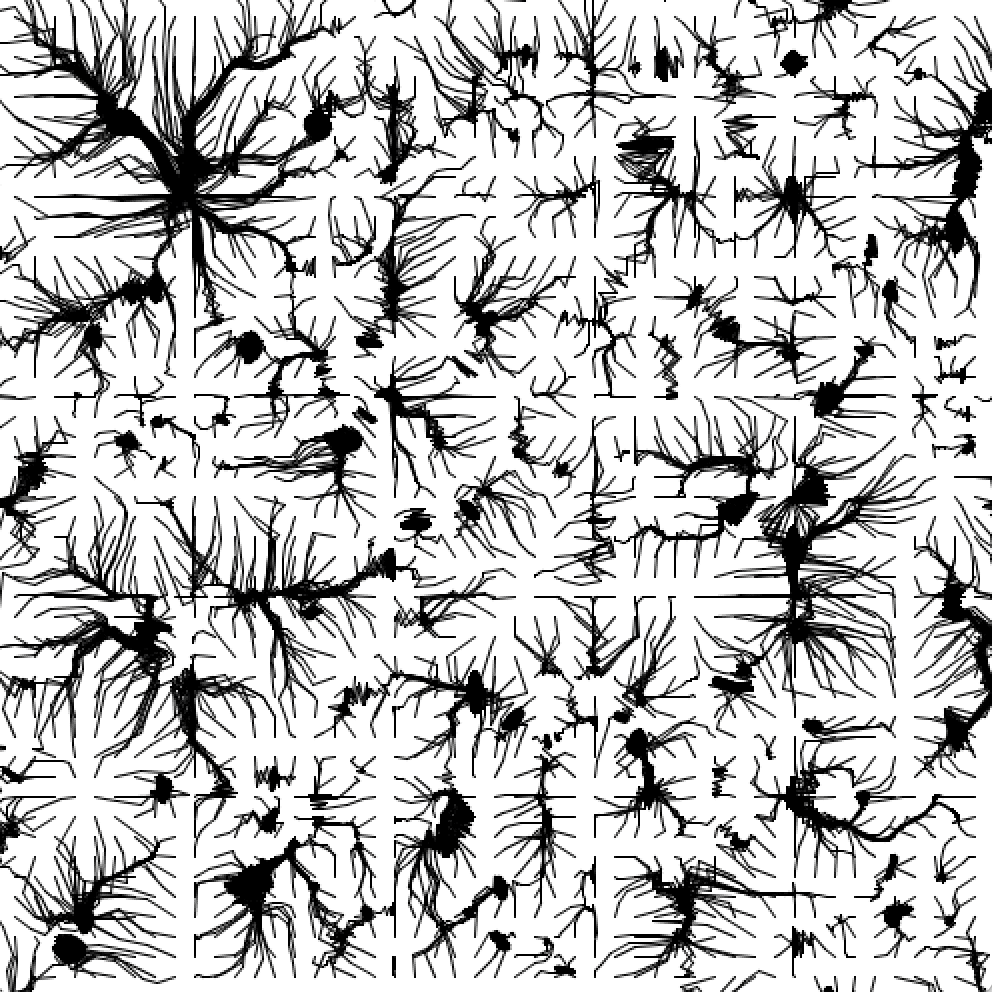

これは、各格子点より出発したとき、ノイズ曲面をどのように登っていくのかを示したものである（変数 e,f の計算の時に加算ではなく減算を行えば、おなじみの最急降下法となる）。

生成された図はなんだか邪悪な雰囲気になってしまった。これはこれで「正しい」絵なんだと思う。が、もう少し魅力的にしたい。

　さて、どうしたものか…と考えていたら、ふと始点計算のところを変調させたらどうだろうか、という考えが浮かぶ。乱数にしても良いのだが、最終的に #つぶやきProcessing 化したいので、random 関数の使用は避けたい（文字数が多いので）。

というわけで、ループ変数を使って適当に変調するコードを書いてみた。変調の状況と数値偏微分の処理が合わないが、ここは気にしない。いろいろ実験することが重要なのである。

実行してみると、横長の作品の方が良さそうなので、横幅も少し広くした。

size(800,500)
background(-1)
for i in range(80*50):
  x=i%80*10;y=i/80*10
  for j in range(100):
    u=x*.00001*i;v=y*.0001*i
    b=noise(u,v)
    s=noise(u+.01,v)-b
    t=noise(u,v+.01)-b
    e=x+s*300;f=y+t*300
    line(x,y,e,f)
    x,y=e,f

良い感じになってきた。なんだかヴォイニッチ手稿のような雰囲気が…うーん、そこまでは言えないか。でもまあ、これまでのものに比べれば面白い絵となったので、今日はこの作品をつぶやき Processing 化する。

　実際に tweet 欄に貼り付けてみると、今日も特にインデントの除去もすることなく、すべて収まってしまった。ということで本日の #AltEdu2022 もお終いとする。


いいなと思ったら応援しよう！