電気について（記事1）

私はペンネーム『電気うなぎ』です。

私は5年前から、産業用蓄電池を取り扱う会社に勤務しています。

電気未経験での入社でしたので、最初は電気のことは何もわからず、まして蓄電池のこともほとんどわからない状態でした。
製造メーカーの資料を読んだりしましたが、すんなりと理解できませんでした。
当然の話ですが、製造メーカーはある程度知識がある人用に資料を作成しています。
そうでないと、基本的なことを一から書かなければならず、膨大な資料になってしまうからです。
ですから、素人から見ると専門的な用語を使って、短い文章で資料作成をします。
ですが簡潔に書いた資料をずっと使い続けるあまり、製造メーカーにも製品の詳細まで把握している人が減ってきます。
ですから、質問をしてもまともな回答が返ってこないことも多々ありました。
そうなると、もう自分で一から調べて理解していくしかありません。

ですから電気未経験者が何がわからず、また何につまずくのかを少しは理解しているつもりです。
ここでは、産業用蓄電池やそれに関連する電気のあれこれについて、書いていきます。
難しい言葉や計算式は、極力使わないつもりです。
読んで頂いた方に、少しでもお役に立てれば幸いです。

電気関連の業界で働いていれば、まず最初に疑問に思うのは電流と電圧について、だと思います。
私は入社当初に電圧と電流について先輩社員から説明して頂きました。
乾電池と豆電球を繋いだ回路図で、乾電池から豆電球に電流が流れると豆電球が点灯する、という説明でした。
私が当時疑問に思ったのは、以下の点です。
・電圧と電流って何？どう違うの？
・電流が豆電球に流れると、なぜ点灯するの？
先輩社員にこれを質問したところ、電気っていうのはそういうものだ。それを疑問に思う必要はない、という回答でした。

それで納得できる人はそれでいいと思います。私のように、それでは嫌だという方用に、この2点について記載していきます。
今はまだピンとこなくてもいいのですが、最初に電圧と電流の定義を記載しておきます。
・電圧とは、単位の大きさの電流が単位時間に行う仕事の量
・電流とは、単位時間当たりに導体のある断面を通過する電荷の量

この説明で理解できる方は、これ以降は読んで頂く必要はないと思います。
時間の無駄ですので。

では、ひとつひとつ順を追ってみていきましょう。
中学校の頃に私が授業で教わった知識は、次のようなものでした。
1.　豆電球に電線とスイッチ(OFF状態)を繋いでそれを乾電池につなげると、電気回路が完成する
2.　スイッチをONにすると電池の正極から負極に向かって電流が流れる。
3.　電流が流れると豆電球が点灯する。
4.　正極から流れて負極に戻ってくる電流の大きさは同じ。

電気の知識がなかった私からすると、この説明を理解するのすら微妙でした。

高校物理では電気の正体である電荷や電位差について学ぶようですが、ここでは一からひとつひとつ見ていきましょう。

〇電流の正体について

まずは電流の正体から見ていきます。
これはもう有名な話ですが、電流の正体は電荷の流れです。
金属中では電子の移動ですし、液体中ではイオンの移動が電流の正体です。
この種類の話をするときには避けて通れないのが、電子や原子のお話です。
まず第一歩として、この電荷について見ていくことにしましょう。

この世に存在するものは極小単位の原子が集まってできています。
この内部を見てみると、中心には原子核があり、その周りに電子というものが存在しています。
原子核内部には、さらに陽子と中性子があります。

陽子には電気的にプラスの性質をもった『電荷』というものがへばり付いています。
同様に電子には電気的にマイナスの性質をもった『電荷』がへばりついています。

この地球が誕生した時に各原子も誕生し、その時に陽子や電子に電荷がくっついたと考えられています。
陽子の電荷の強さによって、原子の種類が変わってきます。
水素原子では陽子が電荷を1 (C)もっているので、電気的につりあうように電子も1個存在します。
陽子の電荷が2 (C)なら、電子は2個存在します。
1 (C)とはなんだ？という話になってきますが、電気素量とよばれるものです。
電荷の単位なんだな、と思って頂ければいいと思います。
基準となる数値です。
電子はこの陽子の周りを、つかずはなれず回っていると考えられています。
陽子は原子内を動けませんが、電子は原子内を動き回れます。
陽子の電荷と電子の電荷が引き合いますが、くっつくことはありません。
電子は陽子に引っ張られながらも陽子の周りを周り続けています。
このように運動をしている物体というのは、それ自体がエネルギーを持っています。

電気的に釣り合った状態の原子から電子が減ると、電気的にはプラスの性質が強くなります。
これを陽イオンと呼んでいます。
逆に電子を多く取り込んだ場合は電気的にマイナスの性質が強くなります。
これを陰イオンと呼んでいます。

ここまでをまとめると、以下のようになります。

・電流の正体は電荷の移動　

実際に電気を流す際には、銅線が頻繁に使われます。
この銅線内では、電流の正体である電荷がどのような動きをしているのかを、見てみましょう。

銅線は銅の金属線を束ねたものを、絶縁体で覆ったものです。
絶縁体とは電気を通しにくい性質をもったものです。
金属は一般的には電気をよく通します。
金属原子は集合すると集合体の中に電子を放出し、陽イオンとなって規則正しく並びます。
この放出された電子を各金属イオンが共有することで、金属は安定した状態になります。

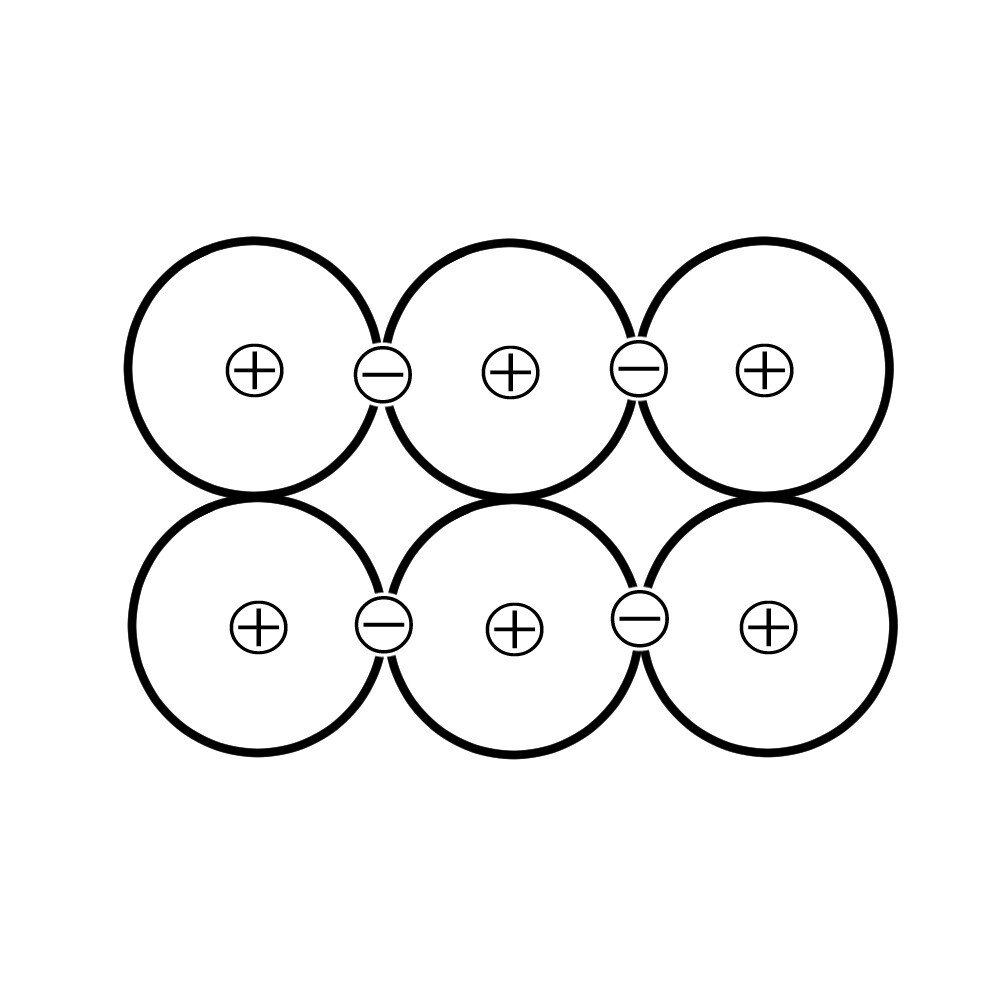
電子を放出すると陽子の持つ正電荷の作用が大きくなります。
そのために電気的にプラスの性質をもったものを陽イオンと呼びます。
放出された電子は、この陽イオンの間を高速で動き回っています。
電子の持つ電荷と陽子の持つ電荷との引き合いと電子自身の持つエネルギーによる運動のためです。
電子とイオンは電気的につり合いが取れているので、金属内では全体として電気的には中性です。

この電子が自由電子と呼ばれるものです。

電気技術者は電源と機器を銅線で接続して電気を通す工事をします。
これが電気技術者がよく扱う電流の正体です、と結論付けてもいいのですが、もう少しだけ詳しく見てみましょう。

〇バンド理論とフェルミ準位

量子力学でみると、原子の周りにはいくつかの軌道があるそうです。
そして軌道ごにエネルギーが決まっている、ということです。
1つの電子はどれかの軌道にいるので、電子が取れるエネルギーは飛び飛びの値になってしまいます。
原子が1個だけの場合を考えてみると、電子のエネルギーに着目するとこんな感じになります。

この中で電子の軌道をエネルギー順に横に書くと、こんな感じになります。

原子内の軌道は2つなのに、横棒では4本じゃないか、というのは気にしないでください。お願いします。
分かりやすいかな、と思って横棒は4本にしちゃいました。

横棒が長いのは、図で書いたために長くなっただけです。
長さには意味はないです。
この横棒のところに電子が居座ることができます。
この横棒のことをエネルギー準位と呼んでいます。
横棒が無いところには、電子は居座ることはできません。

では、原子が複数個あった場合はどうなるでしょうか。
例えば2個の原子を近づけていった場合には、原子間の相互作用が働いて準位が1本から2本に分かれてしまいます。
となると、原子が30個だったら準位も30本に、原子がa個だったら準位もa本に分かれます。
イメージでは、図のようになります。

a本に分かれた準位のエネルギーの差を測定することは不可能です。
見た目でわかると思いますが、この準位の束は連続して分布しており、帯（バンド）のような順位をつくっています。
そのためエネルギーバンドと呼ばれています。
自然の状態で考えると、物体は保持するエネルギーが低い状態が安定していると言えます。
保持しているエネルギーが高いと、エネルギーが低いものに渡そうとして変化しだすので。
物体の中での電子は、エネルギーが低いエネルギーバンドから順番に埋まっていきます。
それが図のような状態です。

図がいっぱいになってしまうのでバンドは3つしか書いていませんが、実際にはもっといっぱいあります。
この図でいうと、一番下のバンドには電子がいっぱいにつまっています。
真ん中のバンドには、電子が半分くらいまでつまっています。
一番上のバンドには、電子はいません。
もうお分かりだとは思いますが、一応最後まで説明しておきます。

一番下のバンドの電子は、もう身動きとれない状態です。
一番上のバンドには、そもそも電子がいません。
真ん中のバンドの電子は、外部からちょっとエネルギーをもらえれば、空いている空間に上がって自由に動き回れそうですね。

常温の物体は、熱のエネルギーを外部からもらっています。
周囲温度が25 ℃であっても、電線内の金属や電子はエネルギーを周囲温度の熱からもらっています。
熱エネルギーをもらった電子は、周りの電子よりも少しだけエネルギーが高い位置へと移動できるため、自由に動き回れるようになります。
この電子が、自由電子と呼ばれるものです。
この電子の移動が、電流と呼ばれるものの正体です。

エネルギーを伝えるために動く電子の割合は、電子全体でみればわずかであると言えます。
それでも個数で言えば無数ですが。

この3本のバンドで考えると、一番上のバンドには電子はほぼ存在しません。
真ん中のバンドには、電子は存在するでしょう。多分。
一番下のバンドには、電子がぎっしり詰まっています。
これは先ほど書いた通りです。
バンドはもっといっぱい存在しますが、その中で電子のいる確率が50 %となる場所をフェルミ準位と呼んでいます。
確率って、なんで？と思いますよね。
電子は目で見えないほどに小さいです。
またあちこち移動します。
ですからどの電子がどこにいるというのを特定することは不可能です。
ですので、電子がこのあたりに居そうだな、という予測を立てるわけです。
このあたりに電子が50 ％の確率で居そうだ、という意味合いです。

上の図を見てもらえれば、もうだいたい分かるかと思います。
荷電子帯とは、原子の最外殻の電子がぎっしりとつまっています。
禁制帯とは、電子が取ることのできないエネルギー帯です。
そして伝導帯にいくと、電子は電気の担い手となれます。

金属の場合は、この境がほぼないです。
そしてフェルミ準位が荷電子帯のすぐ上にあるので、荷電子帯の一部が電気の担い手になれます。

半導体の場合は、外部から何らかのエネルギーを電子に与えてやらないと、電子が荷電子帯から伝導帯に行けません。

絶縁体は、禁制帯の幅が広すぎて、かなりのエネルギーを与えても電子が伝導体へと移動できません。

電子は電気的にマイナスの性質を持ちますので、電気的にプラスと引き合います。
ですから、電気回路中では電子はマイナスからプラスへと流れます。
ですが、『電流』は、プラスからマイナスへと流れます。
ずっと昔、まだ電子や電荷という概念もなかった頃は、『電流』はプラスからマイナスの方向へ流れると考えられてきました。
しかし電子や電荷が発見され、実は電流ではなく電荷が流れていると分かりました。
ですが『電流』のままでも、流れる向きが違うだけで一般的にはあまり実害がないことから、今日でも『電流』という言葉で表現されています。

〇電位差について

電流の正体の次は、電荷に動きを与える力について見ていきましょう。

現在は、こういった考えで運用されている、という考え方の話になります。
電磁気学の話になってしまいますし少しわかりにくいかもしれません。

先ほど話に出た電荷に注目してみます。
今仮に、正電荷を1つ、ある場所にポツンと置いて固定したとします。
正電荷とは、電子を失って電気的にプラスの性質を持ったものです。
するとこの電荷の周りには、電場という力が働きます。
負電荷を引っ張り、正電荷は反発して遠ざけようとする静電気力が働く空間が出来上がる、と考えられています。

そこから少し離れたところに負電荷を置くと、負電荷が引き付けられてくっつきます。

ということは、負電荷は移動する前にはエネルギーを持っていた、ともみなせます。
引き付けられたから動いたんでしょ？となりますが、負電荷が持っていたエネルギーを使って動いてきた、という見方もできるわけです。
つまり、移動前の負電荷は潜在的なエネルギーを持っていたからこそ正電荷のところまで移動できた、とみなせます。
日本ではこれを、位置エネルギーを呼んでいます。
潜在的エネルギーの方が分かりやすい気がしますけど。
1 (C)の正電荷がdメートル進んだときの位置エネルギーのことを、電位と呼んでいます。
このケースでは負電荷が移動しています。
しかし負電荷を固定すれば正電荷が動くのでエネルギーの観点から言えば、同等です。
※実際の銅線などでは正電荷である金属イオンは動けません。
この説明の中では、どちらの電荷が移動したとしても保持している潜在的エネルギーは同等という意味です。

電位というからには、基準点はどこなの？という疑問が浮かぶと思います。
電荷は潜在的なエネルギーをもっていて、それを使って移動します。
このエネルギーを使い切って移動が止まる点が基準点となります。
理論上は、無限遠方です。
しかし電気回路では無限遠方なんて分かりにくい考え方はしません。
基準と比べるというよりは、2点間の電位の差を比べることを意識します。
電位が高い方が、電位の低い方から電荷を引っ張るからです。
電気回路で見れば、電位が高い方へ電子が引っ張られるからです。
この電子の流れが電流です。
ですから、電子や電荷を移動させて仕事をさせる力を与えているのが、電位の差になります。

※電流は電荷の流れとは逆になります。
ですから、電位の高いほうから低いほうへと流れる表記になります。

定義としては、電場の中で1 (C)の正電荷がd メートル移動したときの位置エネルギーが電位でした。
それは1 (C)の負電荷が移動した、と置き換えても、エネルギー的には同じことです。

電線で考えてみましょう。
※先ほどは銅線と呼んでいましたが、電線と呼ぶのが一般的なので。

電線の中には電流の担い手である、電場に反応して動き出せる電子が多数あります。
電線に乾電池をつないだときの電線内部の状態を考えてみましょう。（今は抵抗つまり負荷は除外して考えます）
電池が放電する時には、電池内部の正極では化学反応によって正電荷が発生します。
同様に負極では化学反応によって負電荷が発生します。
電子も余剰に発生します。
すると電池の正極と負極を繋いでいる電線には、電場が発生します。

乾電池の内部で正電荷と負電荷が発生するなら、乾電池内部で引き合ってくっついてしまうのでは？と考えるのが普通ですよね。
ですが乾電池内部では工夫がしてあります。
正電荷と負電荷が内部でくっつかないようになっています。
（詳しくは、これから順次書いていく記事の中で）
乾電池内部で負極から正極へ移動できない電子は、ほかの経路を探して移動します。
低い電圧では、電子は空気中を移動して正極へ至ることはありません。
電気が流れやすい電線をつないでやれば、電子が移動できる経路ができる、ということです。

電線の中の電子が電場を感じると、電子は持っている位置エネルギーを消費して、位置エネルギーが0になる位置まで移動を始めます。
このように、電場内で電荷が持つ位置エネルギーのことを、電位と呼んでいます。
そして、例えばA点の電荷の電位とB点の電荷の電位の差のことを、電圧と呼んでいます。

ここまでが、電圧の説明になります。

前置きがかなり長くなりましたが、これらを踏まえた上で、本題だった中学校の時に教わった以下の状態を詳しくみてみましょう。

〇電気回路中の解説

1.　豆電球に電線とスイッチ(OFF状態)を繋いでそれを乾電池につなげると、電気回路が完成する
2.　スイッチをONにすると電池の正極から負極に向かって電流が流れる。
3.　電流が流れると豆電球が点灯する。
4.　正極から流れて負極に戻ってくる電流の大きさは同じ。

1.　図のように電線を乾電池に繋げると、電子が移動できる路が完成します。
この状態では電子は移動しませんが、スイッチがONされるのを今か今かと待っているようないないような、そんな状態です。

2.　スイッチをONにすると乾電池の中で化学反応が起き、正極では正電荷が、負極では負電荷の電子が多くなります。
また電線内も金属ですので、その内部は金属イオンが規則正しく並んでいます。そしてその間に電子が存在しています。

いざ電気回路に電圧がかかれば、これらの電子が正極へと引っ張られます。その際に電子はさまざまな方向へ移動しながら正極へと向かいます。
金属イオンは動けませんので、ある電子はこの金属イオンにぶつかり、またある電子同士はぶつかる前に反発して向きを変えながら移動します。
ぶつかった電子は、そのエネルギーを金属イオンに渡します。
エネルギーをもらった金属イオンは振動し、それを熱として放出します。
電子が電線を流れると熱くなるのは、このためです。
部分部分をみれば電子はさまざまな動きをしますが、全体でみれば電子は一定の向きと速度で正極へと向かっていくとみなせます。
電線内には無数の電子が存在しているため、電圧をかけるとこの電子がいっせいに動き出します。
隣り合った電子がぶつかったり押し出されたりするのではなく、動くことができる電子すべてがいっせいに動くのです。

3.　の状態を考える前に、豆電球が点灯する直前までの状態を見てみましょう。
電池の負極の電子は乾電池の正極に1.2 ボルトの力で引っ張られます。
ということは、負極の電子は位置エネルギー（潜在エネルギー）を保持していることになります。
また電線を負極に接続することで、豆電球手前までの電線内の電子も位置エネルギーを保持していることになります。
トータルでみれば、電線内の金属イオンにぶつかって渡したエネルギーは損失となりますので、それを引いた分のエネルギー、ということになります。
この無数の電子が豆電球に到達するわけです。

豆電球というのは、ガラス管の中を真空にしてその中に細くしたタングステン製のフィラメントを配置したものです。

この細いフィラメントの中を、エネルギーを持った電子が通るとその中の金属イオンとぶつかります。
電線よりも断然細いタングステンですから、電子は電線中を通る時よりもずっと多く金属イオンと衝突します。
この衝突により電子のもつエネルギーが金属イオンへと受け渡されます。
金属イオンがエネルギーをもつと、激しく振動を始めます。すると熱が発生します。
豆電球でも2,000～3,000 ℃の高温になり、光を発生するという具合です。
豆電球中は真空ですから、タングステンが高温になっても酸素が無く燃えることはありません。
豆電球を通過した電子は、もっていたエネルギーの大半を失います。
そして豆電球を通過したところでまた引っ張られて正極へ向かう、ということになります。
電子が負極を出発してから正極へ到達するまでを考えると、負極を出発する瞬間に持っていた潜在的エネルギーは、正極に到達すると0になると考えることができます。
電子のもつ潜在的エネルギーは、正極に到達するまでに失われたエネルギーの総量と同じだと考えられますよ、ということです。
トータルでみると、負極を出発して電線内の金属イオンとぶつかって一部のエネルギーを失い、また豆電球内のタングステンとぶつかりエネルギーを失い、そして豆電球を出た後でも電線内の金属イオンとぶつかってエネルギーを失い、ようやく正極へたどり着く頃にはすべてのエネルギーを失うと考えられます。

※補足です。
電子がどの程度のエネルギーをもつのかは、eV（電子ボルト）を使って表されます。
1 eVとは、1 Vの電位差で電子1個を加速させたときに、電子が得る運動エネルギーのことです。
1 eV を温度に換算すると、10000 K（ケルビン）です。
およそ10273℃になります。
電子が銅線を移動する際には、金属イオンにぶつかってこの熱を放出します。
電球内のフィラメントがあんなに高温になるのも、電子がこれだけのエネルギーをもっているからです。

4.　電線を移動する電子の数は同じです。
ですが、その電子の持つエネルギーは、豆電球を通過する前と後では違います。
私が電気の仕事に就いた時は、出ていく数と戻る数が同じなのに、なぜ豆電球が点灯するのかが疑問でした。
ですが、エネルギーを運ぶ頭数は同じだけど途中でエネルギーを受け渡しているんだと考えると、腑に落ちました。

また、この電気回路でスイッチをONにした瞬間に豆電球が点灯します。
しかしそんなに一瞬で電子が動いてエネルギーを与えられるものなのか、という疑問も浮かびました。
このあたりの説明は、電場と磁場が関係してくると考えられています。
電磁場が高速で、電線内の動ける電子にいっせいに伝わるために、電子がいっせいに向きを変え一瞬にして豆電球が点灯する、ということになります。
（この話になると難しいので、説明がうまくできずで、すいません。）
個別の電子に注目すればいろいろな動きをしていると思いますが、全体としてみれば、という話です。

ちなみに、電気回路には電圧をかける前に必ず負荷を接続しないと危険です。
今の説明の場合は、豆電球を負荷として接続しています。
豆電球を接続していれば、電気回路に電圧をかけてもそのエネルギーは豆電球で消費されます。
ですが豆電球を接続しておらず、電線のみで正極と負極を接続した場合は、危険です。
まあ乾電池1.2 ボルトくらいでは、何も起きないと思いますが。
家庭用のコンセント100 ボルトのプラスとマイナスを電線のみで接続した場合は、危険です。
負荷を接続していない場合、エネルギーは電気回路の中で一番抵抗が高いところで消費されます。
電線の細い部分や接触面積が小さい部分は電子が他の部分よりも通りにくいために、そこで金属イオンと接触する回数が増えます。
そしてその際に発熱し、高温になり焼けます。
俗にいう短絡事故です。
回路の接続の際には、短絡事故には注意してください。

電圧と電流に関しての説明は、以上になります。

〇オームの法則について

ここからは、余談になります。

電気回路では電圧、電流のほかにもう一つ、抵抗という言葉が出てきます。
電気エネルギーを消費する電気部品を指すことが多いです。
また、負荷と呼ぶこともあります。

電気回路では、オームの法則が成り立ちます。
電圧(V) ＝ 電流(A) × 抵抗(Ω)

・100 V ＝ 10 A ×10 Ω　となるわけですね。

10 Ωの抵抗に100 Vの電圧をかけると、10 A流れますよ、ということです。
別の見方をするなら、こうなります。
10 Ωの抵抗に10 Aの電流が流れ込む前と後では、100 Vの電位の差が生まれますよ、とも考えられます。
抵抗で電気エネルギーが消費されて、電位に差ができます。
そのエネルギー輸送に必要な電流の大きさが、10 Aですよ、ということですね。

また電気回路では、電線もその内部に電気抵抗を持っています。
つまり電気を流せば電気エネルギーを消費して、熱として放出します。
結果的に、電線に電気を流す前と流した後でも電位に差が生じます。
電源から抵抗へ伸びた電線と、抵抗から電源へ戻る電線でそれぞれエネルギーが消費されるわけです。
仮に電線の内部抵抗を1 Ωとすれば、回路全体の電線の抵抗は2 Ωになります。
よって抵抗にかかる電圧は、電源電圧よりも下がります。
電線で消費された電位分だけ、下がるわけです。
これを電圧降下と呼んでいます。

つまり上の式は、実際にはこうなるわけです。
・100 V ＝ 8.33 A × [10 Ω + 2 Ω (電線抵抗1 Ω × 2本 ) ]
ですが学校の試験等では、指定されない限りこの電線の電圧降下は考慮していません。
実際の現場では、電線が長くなればこの電圧降下が無視できませんので、考慮する必要があります。

・100 V ＝ 5 A × ( 10 Ω + 10 Ω ）
　　　   ＝ (5 A ×10 Ω ) + (5 A × 10 Ω )
　　　   ＝ 50 V + 50 V　
という関係も成り立ちます。

抵抗それぞれにかかる電圧は、先ほどとは変わり50 Vになります。
電流も、先ほどとは変わり半分の5 Aになります。
電源から各抵抗へ供給される電気エネルギーが、抵抗1 個の時と比べると半分になったということです。
当然ですが、抵抗の前後でも電位の差は半分の50 Vになります。

・100 V ＝100 A × 1 Ω　という関係にもなります。
これだと、抵抗部分で相当発熱しそうですね。
それに電気回路に電気エネルギー100 Aの大きさ分が流れるので、それに耐えられる太さの電線にしなくてはいけません。
というよりは、10 V ＝ 10 A × 1 Ωでいいんじゃないの？危ないし。
といって回路の見直しをしたほうがいい、ということに気付けます。
使用する電線と長さによってはその全長で1 Ω程度になることもあります。
もう少し大きいかもしれませんが。
つまり、100 Vの電源に対して1 Ωの抵抗とは、電気回路にほぼなんの負荷も接続していないに等しいです。
ですから抵抗部分で相当発熱しますし、場合によっては抵抗が燃えます。

・100 V ＝ 1A × 100 Ω　という関係にもなります。
バンド理論で書きましたが、この抵抗はフェルミ準位に、自由に動ける電子がごくわずかしかない物質になります。
つまり100 Vの電圧で電子を引っ張ろうにも、そもそも抵抗の内部に電気の担い手になる電子が少ない、ということです。
100 Vで引っ張ってやっと流れる、というイメージですね。
ですから電気エネルギーは消費しますが、流れる電流の大きさは1 Aだけです、ということです。
電流の流れる量を増やしたいなら、電圧を上げるしかありません。

電気回路では、実際にどんな回路を組むかによって抵抗にかかる電圧の大きさや流れる電流値が変化します。
回路全体に供給できる電気エネルギーは抵抗の大きさに対応して分配される、ということです。
そしてその分配のルールを表しているのが、オームの法則ということになります。