テンバガー株価予測をPythonでやってみた結果。
はじめに
テンバガーの分析方法
テンバガーの予測(結論)
今後の株価予測(一部抜粋)
最後に
はじめに
2022年8月現在、プログラミングスクールAidemyにてPythonの学習をしている中で、株式の予測ができることを知り、少額ではあるが、毎月こつこつと米国株式に投資をしている私からすると、一度取り組みたい内容でした。
※ブログ執筆時期は同様に2022年8月のため、あくまで私の備忘録が目的です。投資は個人の判断で行ってくださいませ。
テンバガーの分析方法
色々なサイトを見た結果、以下の5点を基準にスクリーニングをかけていく。また今回は私が普段使用しているSBI証券でのスクリーニングになります。
まず4つのスクリーニングで約5000銘柄から64銘柄まで絞り込む
1、時価総額500億円以下
2、自己資本比率25%以上
3、実績益利回り15%以上
4、実績売上高変化率15%以上
さらに1株10ドル以上という条件を追加することで、64銘柄から19銘柄まで絞り込む。
絞り込んだ結果、以下の銘柄にまとまりましたので、実際に分析していきたいと思います。
tenbagger_list = ['ARKR','AVNW','AWX','BBW','BDL','EDRY','ESEA',
'FINW','FLXS','FRD','GRIN','ITIC','LAZY','LIVE',
'NAII','NC','STRT','SYNL','ZEUS']テンバガーの予測(結論)

上の図を参考に、テンバガーになる可能性がある銘柄を分類します。
・ローリスクローリターン
AVNW,SYNL,ARKR
・ハイリスクローリターン
LIVE,ESEA,BBW,EDRY
・ハイリスクハイリターン
ZEUS,NC,GRIN
ということが表示されました。
ではいよいよ、最初から解析していきます。また上記の図以降の詳しい分析も行っていきますので、最後まで読んでみてください。
必要なデータを読み込む
# 必要なライブラリをimportします
import pandas as pd
from pandas import Series,DataFrame
import numpy as np
# 可視化のためのセットです。
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('whitegrid')
%matplotlib inline
# Yahooからデータを読み込めるようにします
import pandas_datareader as pdr
# Pythonで日付と時刻を扱うためのモジュールです
from datetime import datetime
# テンバガーの予測を行います
tenbagger_list = ['ARKR','AVNW','AWX','BBW','BDL','EDRY','ESEA',
'FINW','FLXS','FRD','GRIN','ITIC','LAZY','LIVE',
'NAII','NC','STRT','SYNL','ZEUS']
# 直近2年間のデータを使ってみましょう。
end = datetime.now()
start = datetime(end.year - 2,end.month,end.day)
# それぞれの企業ごとに、Yahooのサイトからデータを取得します
for stock in tenbagger_list:
# それぞれの名前でDataFrameを作ります。
globals()[stock] = pdr.DataReader(stock, 'yahoo', start, end) 試しにデータを見てみましょう。

過去2年間の株価を一部抜粋します。


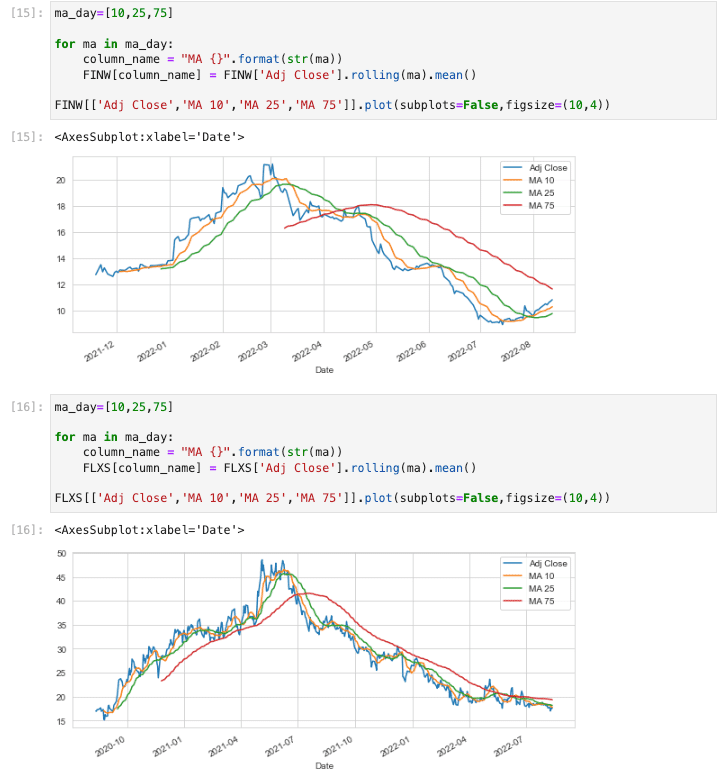
株を勉強したことがあれば、恐らく移動平均線を見ると思われます。
今回は一部抜粋ではございますが、ゴールデンクロスが出て株価が上がっている銘柄、これからゴールデンクロスが出そうな銘柄、ゴールデンクロスの前兆が見えにくい銘柄がございました。
ただ、私が抜粋した銘柄の多くは、ゴールデンクロスが出た後もしくはこれから出そうな銘柄でした。
リスクを分析してみます。
closing_df = pdr.DataReader(['ARKR','AVNW','BBW','BDL','AWX','EDRY','ESEA',
'FINW','FLXS','FRD','GRIN','ITIC','LAZY','LIVE',
'NAII','NC','STRT','SYNL','ZEUS'],'yahoo',start,end)['Adj Close']
# 別のDataFrameにしておきます。
tech_rets = closing_df.pct_change()
# リスクの基本はその株価の変動幅です。
rets = tech_rets.dropna()
rets.head()
area = np.pi*20
plt.scatter(rets.mean(), rets.std(),alpha = 0.5,s =area)
plt.ylim([0.01,0.060])
plt.xlim([-0.005,0.005])
#Set the plot axis titles
plt.xlabel('Expected returns')
plt.ylabel('Risk')
# グラフにアノテーションを付けます
for label, x, y in zip(rets.columns, rets.mean(), rets.std()):
plt.annotate(
label,
xy = (x, y), xytext = (0, 2),
textcoords = 'offset points', ha = 'right',
arrowprops = dict(arrowstyle='-', connectionstyle= 'arc3'))ということで結論のスクショまできました。

今後の株価予測(一部抜粋)
さて、ここまでは過去から現在までの株価からデータを見てきましたが、これからは今後の株価予測を行い、結果によっては私も少ないお小遣いを捻出しようと思う。
# 1年を基準にします。
days = 365
# 1日分の差分です。
dt = 1/days
# 日々の変動の平均を計算します。
mu = rets.mean()['ARKR']
# ボラティリティ(volatility:株価の変動の振れ幅)を変動の標準偏差で計算します。
sigma = rets.std()['ARKR']
def stock_monte_carlo(start_price,days,mu,sigma):
''' この関数は、シミュレーションの結果の価格リストを返します。'''
# 戻り値となる価格のリストを返します。
price = np.zeros(days)
price[0] = start_price
# Shock と Driftです。
shock = np.zeros(days)
drift = np.zeros(days)
# 指定された日数のところまで、計算します。
for x in range(1,days):
# shockを計算します
shock[x] = np.random.normal(loc=mu * dt, scale=sigma * np.sqrt(dt))
# Driftを計算します。
drift[x] = mu * dt
# これらを使って価格を計算します。
price[x] = price[x-1] + (price[x-1] * (drift[x] + shock[x]))
return price
# 最初の終値から始めます。
start_price = AVNW.iloc[0,5]
for run in range(5):
plt.plot(stock_monte_carlo(start_price,days,mu,sigma))
plt.xlabel("Days")
plt.ylabel("Price")
plt.title('Monte Carlo Analysis for AVNW')
ローリスクローリターン
上記の図よりAVNW社の場合、1年後の株価予測が5本中4本が上がる予測をしています。
上記にも記しましたが、AVNW社はローリスクローリターンのため、まーこんなもんかという印象です。
ハイリスクローリターン

EDRY社はハイリスクローリターンに分類されましたが、1本の予測以外現状維持の予測が出ています。
ハイリスクハイリターン

ハイリスクハイリターンに分類したNC社とGRIN社ですが、ハイリスクハイリターンの名前に恥じない、見事は値動きの暴れ具合です。ただ、GRIN社の方が総じて値上がりの予測になっていますので、この図だけで判断するのであればGRIN社の方が値下がりのリスクは少ないかもしれません。
全コード掲載します。
このままコピペしても、上手く図が表示されませんので、こまめに分割してください。
# 必要なライブラリをimportします
import pandas as pd
from pandas import Series,DataFrame
import numpy as np
# 可視化のためのセットです。
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('whitegrid')
%matplotlib inline
# Yahooからデータを読み込めるようにします
import pandas_datareader as pdr
# Pythonで日付と時刻を扱うためのモジュールです
from datetime import datetime
# テンバガーの予測を行います
tenbagger_list = ['ARKR','AVNW','AWX','BBW','BDL','EDRY','ESEA',
'FINW','FLXS','FRD','GRIN','ITIC','LAZY','LIVE',
'NAII','NC','STRT','SYNL','ZEUS']
# 直近2年間のデータを使ってみましょう。
end = datetime.now()
start = datetime(end.year - 2,end.month,end.day)
# それぞれの企業ごとに、Yahooのサイトからデータを取得します
for stock in tenbagger_list:
# それぞれの名前でDataFrameを作ります。
globals()[stock] = pdr.DataReader(stock, 'yahoo', start, end)
ARKR.describe()
# 間隔ごとに移動平均を描いてみます。
ma_day=[10,25,75]
for ma in ma_day:
column_name = "MA {}".format(str(ma))
# AAPL[column_name]=pd.rolling_mean(AAPL['Adj Close'],ma)
#@ 移動平均を求めるやり方がわかりました。以下のように書きます。
#銘柄を変えてください。
ARKR[column_name] = ARKR['Adj Close'].rolling(ma).mean()
ARKR[['Adj Close','MA 10','MA 25','MA 75']].plot(subplots=False,figsize=(10,4))
#@ pandas_datareaderを使います。
closing_df = pdr.DataReader(['ARKR','AVNW','BBW','BDL','AWX','EDRY','ESEA',
'FINW','FLXS','FRD','GRIN','ITIC','LAZY','LIVE',
'NAII','NC','STRT','SYNL','ZEUS'],'yahoo',start,end)['Adj Close']
# 別のDataFrameにしておきます。
tech_rets = closing_df.pct_change()
# リスクの基本はその株価の変動幅です。
rets = tech_rets.dropna()
rets.head()
area = np.pi*20
plt.scatter(rets.mean(), rets.std(),alpha = 0.5,s =area)
plt.ylim([0.01,0.060])
plt.xlim([-0.005,0.005])
#Set the plot axis titles
plt.xlabel('Expected returns')
plt.ylabel('Risk')
# グラフにアノテーションを付けます
for label, x, y in zip(rets.columns, rets.mean(), rets.std()):
plt.annotate(
label,
xy = (x, y), xytext = (0, 2),
textcoords = 'offset points', ha = 'right',
arrowprops = dict(arrowstyle='-', connectionstyle= 'arc3'))
# 1年を基準にします。
days = 365
# 1日分の差分です。
dt = 1/days
# 日々の変動の平均を計算します。
mu = rets.mean()['ARKR']
# ボラティリティ(volatility:株価の変動の振れ幅)を変動の標準偏差で計算します。
sigma = rets.std()['ARKR']
def stock_monte_carlo(start_price,days,mu,sigma):
''' この関数は、シミュレーションの結果の価格リストを返します。'''
# 戻り値となる価格のリストを返します。
price = np.zeros(days)
price[0] = start_price
# Shock と Driftです。
shock = np.zeros(days)
drift = np.zeros(days)
# 指定された日数のところまで、計算します。
for x in range(1,days):
# shockを計算します
shock[x] = np.random.normal(loc=mu * dt, scale=sigma * np.sqrt(dt))
# Driftを計算します。
drift[x] = mu * dt
# これらを使って価格を計算します。
price[x] = price[x-1] + (price[x-1] * (drift[x] + shock[x]))
return price
ARKR.head()
ARKR.iloc[0,5]
# 最初の終値から始めます。銘柄を変更してください。
start_price = AVNW.iloc[0,5]
for run in range(5):
plt.plot(stock_monte_carlo(start_price,days,mu,sigma))
plt.xlabel("Days")
plt.ylabel("Price")
plt.title('Monte Carlo Analysis for AVNW')最後に
今回はPythonを用いた株価のデータ解析を行いました。今回勉強したことを私の投資生活にも応用していきたいと思います。
今後はこれを発展させて、銘柄を検索したらこういったデータを出してくれるアプリ開発もできたらおもしろそうですね。
この記事が気に入ったらサポートをしてみませんか?
