【Tableau初学者(Python復習)】Kaggle : Japan Life Expectancy
使用環境
Macbook Air (M1)
Google Colaboratory
目的
データ分析について学習しつつも、BIツール(Tableau )に触れたことがなかったので、学習してみたいと思い、Kaggleにあった「Japan life expectancy」を教材に、Pythonの復習も兼ねてスキルの習得を目指す。
実践内容
1.Python編
1-1. データセットの取得
・Kaggleにある「Japan life expectancy」のデータセットを拝借
1-2. データ読み込み(中身の確認)
・データの読み込み(中身の確認)
#データの読み込み
import pandas as pd
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
df = pd.read_csv(pass)
df
#欠損値の確認
print(df.isna().any())
#データ形式の確認
df.dtypes
【特徴量について】
1.Prefecture : 県名
2.Life_expectancy : 平均寿命 (単位:年)
3.Physician : 医療施設で働いている医師の数(人口10万人あたり)
4.Junior_col : 短大相当を卒業した人の割合[%]
5.University : 大学まで卒業した人の割合[%]
6.Public_Hosp : 公立総合病院の割合[%]
7.Pshic_Hosp : 精神病院の数(人口10万人あたり)
8.Beds_psic : 精神疾患病床数(人口10万人あたり)
9.Nurses : 医療機関に勤務する看護師・准看護師数(人口10万人あたり)
10.Avg_hours : 労働時間(月平均)
11.Salary:フルタイム勤務の給料
12.Elementary_school : 小学校または中学校までのみを卒業した人の割合(%)
13.Sport_fac : スポーツ施設の数(人口10万人あたり)
14.Park : 自然公園の面積の割合(土地総面積に対する割合)[%]
15.Forest : 森林面積の割合(土地総面積に対する割合) [%]
16.Income_per capita : 1人当たりの県民所得(2011年基準)
17.Density_pop : 人口密度 (1キロ平方メートル当たり)
18.Hospitals : 総合病院の数(人口10万人あたり)
19.Beds : 総合病院の病床数(人口10万人あたり)
20.Ambulances : 救急車の台数(人口10万人あたり)
21.Health_exp : 各都道府県の医療費の占める割合[%]
22.Educ_exp : 各都道府県の教育費の占める割合[%]
23.Walfare_exp : 各都道府県の生活保護費の占める割合[%]
1-3. データの抽出、可視化
・各特徴量の相関を確認し、可視化
#相関係数ヒートマップの作成
fig, ax=plt.subplots(1,1, figsize=(20,15))
sns.heatmap(df.corr(), annot=True, linewidths=1)
plt.show()
更にこの中から、平均寿命と「やや相関がある(=相関係数0.4~)」以上の特徴量を抽出すると、
#相関係数0.4以上を抽出
threshold = 0.4
cmap = sns.diverging_palette(220, 10, as_cmap=True)
fig, ax = plt.subplots(figsize=(20, 15))
sns.heatmap(correlation_matrix, annot=True, linewidth=1, cmap=cmap, vmin=1, vmax=1, mask=correlation_matrix.abs() <= threshold)
plt.show()
①大学を卒業した人
#Universityの散布図作成
uni_correlation = df["Life_expectancy"].corr(df["University"])
plt.scatter(x=df["University"], y=df["Life_expectancy"])
plt.xlabel("University")
plt.ylabel("Life_expectancy")
plt.title("Life_expectancy vs University")
plt.show()
uni_correlation
②短大相当を卒業した人
#短大相当を卒業した人の散布図作成
juni_correlation = df["Life_expectancy"].corr(df["Junior_col"])
plt.scatter(x=df["Junior_col"], y=df["Life_expectancy"])
plt.xlabel("Junior_col")
plt.ylabel("Life_expectancy")
plt.title("Life_expectancy vs Junior_col")
plt.show()
juni_correlation
③小学校または中学校を卒業した人
#小学校または中学校を卒業した人の散布図
Elementary_correlation = df["Life_expectancy"].corr(df["Elementary_school"])
plt.scatter(x=df["Elementary_school"], y=df["Life_expectancy"])
plt.xlabel("Elementaly_school")
plt.ylabel("Life_expectancy")
plt.title("Life_expectancy vs Elementaly_school")
plt.show()
Elementary_correlation
④フルタイム勤務の給料
#フルタイム勤務の給料の散布図
sala_correlation = df["Life_expectancy"].corr(df["Salary"])
plt.scatter(x=df["Salary"], y=df["Life_expectancy"])
plt.xlabel("Salary")
plt.ylabel("Life_expectancy")
plt.title("Life_expectancy vs Salary")
plt.show()
sala_correlation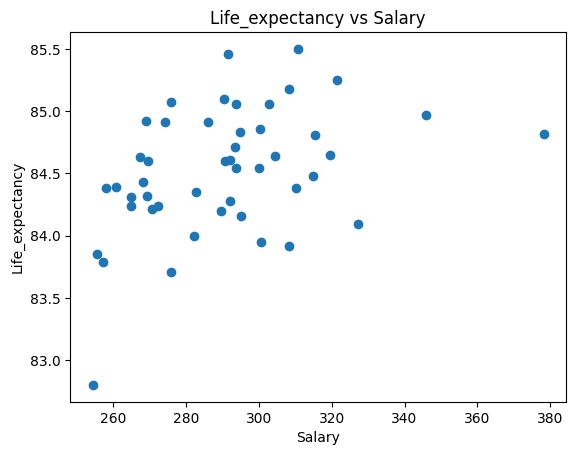
には平均寿命と「やや相関がある」以上の関係があることが分かった。特に、③「小学校または中学校を卒業した人」については負の相関がある。
ここで、平均寿命のTop_5とBottom_5を抽出してみると、
Top_5では5県中4県が関西地方にあり、Bottom_5では5県中4県が東北地方に存在していることが分かった。
#平均寿命のTop_5とWorst_5を抽出し、平均寿命の降順に並べる
top_5 = df.sort_values(by="Life_expectancy", ascending=False).head(5)
bottom_5 = df.sort_values(by="Life_expectancy").head(5)
result = pd.concat([top_5, bottom_5], axis=0)
sorted_result = result.sort_values(by="Life_expectancy", ascending=False)
sorted_result
これらの抽出した地域と各学歴のTop_5とBottom_5について調べてみる。
①-1 大学卒業した人の割合 Top_5
→平均寿命Top_5のうち1県(奈良)が入っている

①-2 大学卒業した人の割合 Bottom_5
→平均寿命Bottom_5のうち4県(青森、秋田、岩手、福島)が入っている

②-1 短大相当を卒業した人 Top_5
→平均寿命Top_5のうち2県(長野、奈良)が入っている

②-2 短大相当を卒業した人 Bottom_5
→平均寿命Bottom_5のうち3県(秋田、青森、福島)が入っている。

③-1 小学校または中学校を卒業した人の割合 Top_5
→平均寿命Bottom_5のうち3県(青森、秋田、岩手)が入っている。

③-2 小学校または中学校を卒業した人の割合 Bottom_5
→平均寿命Top_5のうち1県(奈良)が入っている。

④-1 フルタイム勤務の給料Top_5
→平均寿命Top_5のうち1府(京都)が入っている。

④-2 フルタイム勤務の給料Bottom_5
→平均寿命Bottom _5のうち3県(青森、岩手、秋田)が入っている。

1-4. Python編 まとめ
・Python編 まとめ
今回はデータセットに欠損がなく、綺麗な状態のデータだったので、クレンジングすることなく、抽出のみで可視化することができた。
ここまでの調査をまとめると、フルタイム勤務での給料と平均寿命との関係はあまり高くないが、平均寿命と学歴にはやや相関があり、学歴が高い程平均寿命が長く、学歴が低いと平均寿命が短い可能性がある。
関西と東北の地域の違いによる平均寿命との相関もありそうではあるが、最初に示した平均寿命と各特徴量の相関係数の表より、今回のデータセットにある情報では学歴意外の相関関係は見られない。
地域性についてはデータセット以外にも他の情報を取り入れることができれば、より明確な関係性が見えてくるのではないかと考えられる。
2.Tableau編
2-1.データセットの取得
・Python編で使用した物と同じデータセットを使用
2-2.データの読み込み
・Python編で使用したものと同じcsvデータをTableauに読み込む

2-3.データの抽出、可視化
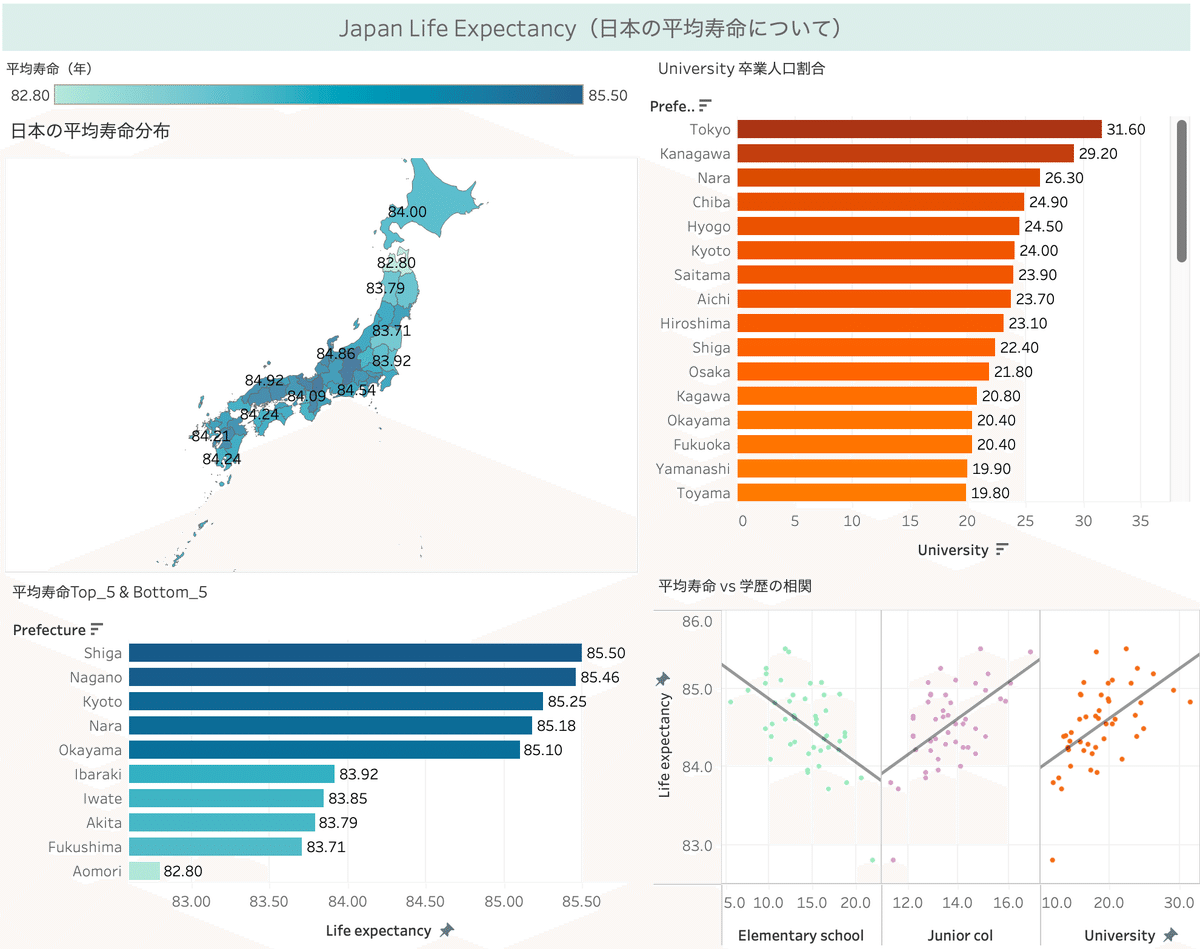
・データセットの平均寿命(Life expectancy)と都道府県(Prefecture)のデータを使い、全国での平均寿命の分布を可視化してみる。

・平均寿命の都道府県Top_5とBottom_5を抽出

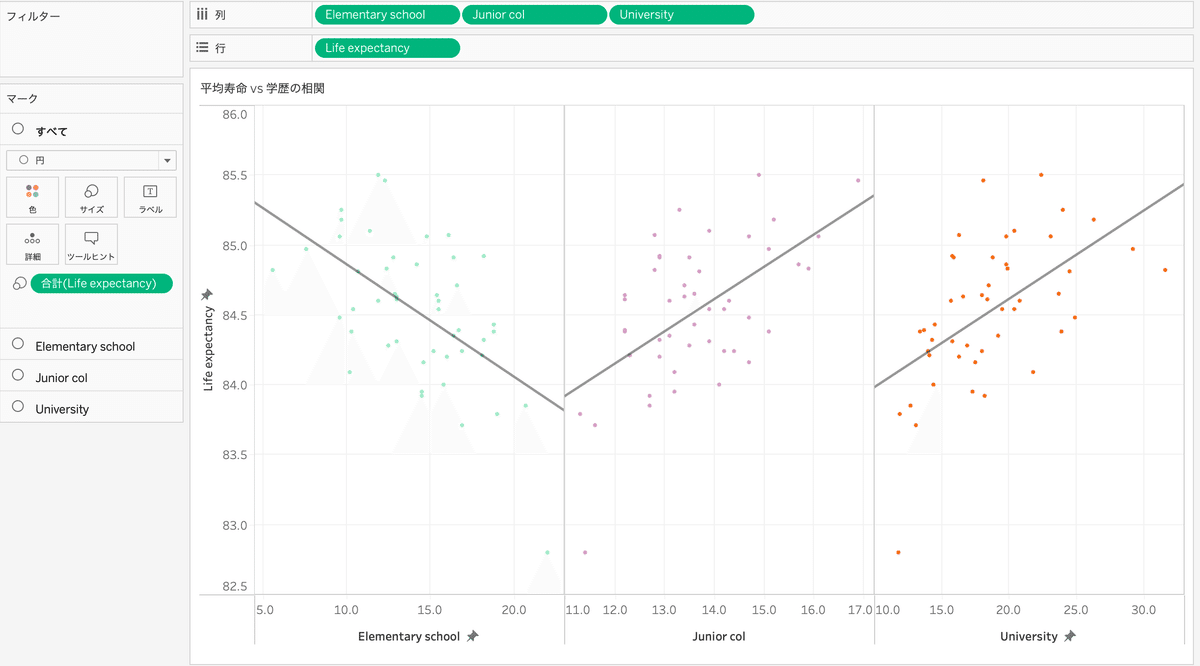
・Pythonの時と同じように、平均寿命と各学歴での相関を可視化
→小・中学校までの卒業では負の相関、大学卒業との相関では正の相関が同じように確認できた。
・高い学歴(=大学卒業した人の割合)を都道府県でランキング化

・ダッシュボードを作成
2-4. Tableau編 まとめ
今回始めてTableauを使ってみたが、プログラムコードと違いソフトとして完成されているので、機械設計のCADソフト使っているような、それに近い感覚で直感的に操作することができた。
計算フィールドでSQLも使えるので、条件式の組み合わせでより細かい抽出ができると感じた。
ダッシュボードにおいてはある程度決まったフォーマットもありつつ、各お客様に向けてそれぞれカスタマイズできるのも面白みの1つだと感じた。
また、他の方のコンテスト作品等を見ると、ただ分析結果をまとめるだけでなく、個性溢れた表現をすることもできると知り、より興味を持つことができた。
実際に仕事として作成する際には、お客様とのコミュニケーションを通じてどんなアウトプットが求められているのか、それに合わせてどんな表現で作り上げていくのがベストなのかを考えながら作り上げていく事になると思うので、その点に関しても機械設計と通じるものがあると感じた。
Python編でも述べたように、今回はデータが綺麗な状態だったので、次はデータクレンジングも含めてもっと複雑なデータを扱えるように、精進していく。
この記事が気に入ったらサポートをしてみませんか?
