
【W4】リガンドベーススクリーニング_02_Step1_Morganフィンガープリント
【本パート(W4)の目的】
化合物をエンコード(記述子、フィンガープリント)し、比較(類似性評価)する様々なアプローチを取り扱います。さらに、バーチャルスクリーニングを実施します。
上記はPython版のT4の説明ですが、W4の目的も同じです。
そのための教材として
既知のEGFR阻害剤ゲフィチニブ(Gefitinib)をクエリとして使用し、EGFRに対して試験済みの化合物データセットの中から類似した化合物を検索します。
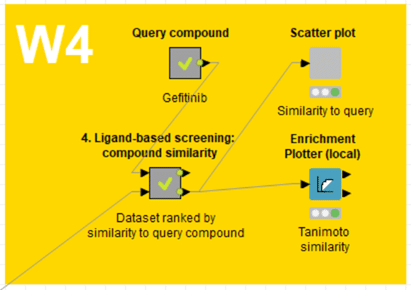
【入力データ確認】
類似度計算に用いる化合物データは、
上図のQuery compoundメタノードで入力したGefitinibと
デモデータに用いる化合物群としてはW2の出力である4510化合物です。
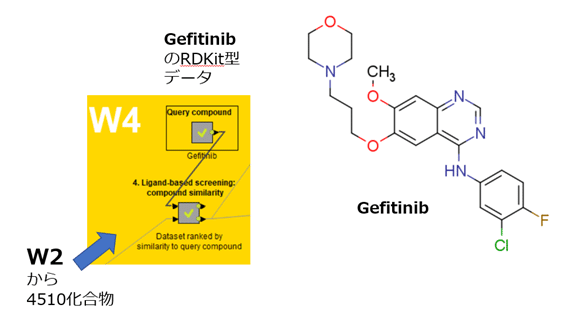
【Query compoundメタノード】
中身は下図の通り。
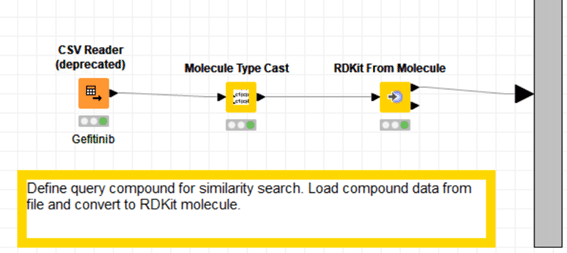
W3で紹介したノードばかりなので、詳細は省きます。
今回はcsvファイルからどんなデータが入力されたかだけ以下に示します。
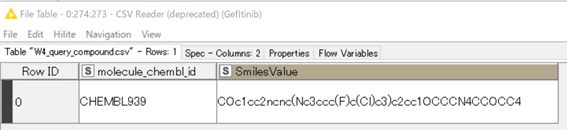
余談ですが後日Marvin 化合物名で設定する方法も紹介予定です。
【フィンガープリント算出】
KNIME workflowでは
「4. Ligand-based screening: compound similarity」メタノード内のStep1
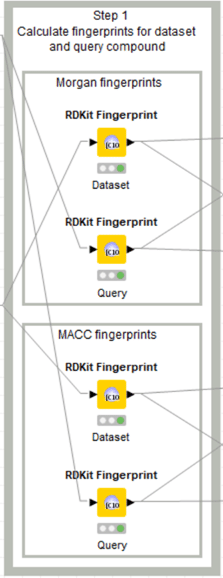
今回はStep1の上部, Morganフィンガープリント算出を体験します。
【Morganフィンガープリント】
Mishima.sykの皆さんによる説明を紹介します。
フィンガープリントとは分子の部分構造を0,1のバイナリーで表現したもので部分構造の有無とビットのon(1),off(0)を対応させたものになり、部分構造の集合を表現することで分子の特徴を表現しています。フィンガープリントには固定長FPと可変長FPの二種類が存在し、古くはMACCS keyという固定長FP(予め部分構造とインデックスが決められているFP)が使われていましたが、現在ではECFP4(Morgan2)という可変長FPが利用されるのが普通です。
RDKitのフィンガープリントに関しては開発者のGregさんのスライドが詳しいので熟読してください。
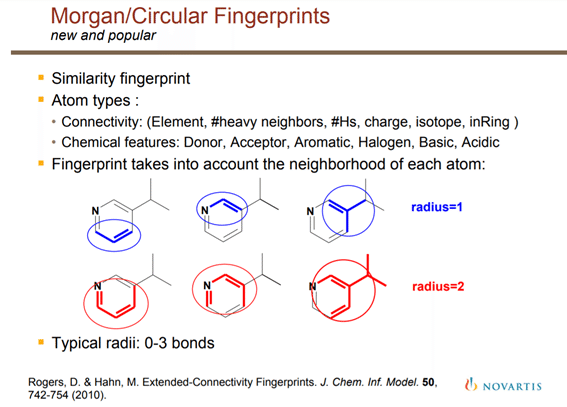
(引用元)https://www.rdkit.org/UGM/2012/Landrum_RDKit_UGM.Fingerprints.Final.pptx.pdf
【ECFP/FCFPフィンガープリントとMorganフィンガープリント】
恥ずかしながら「KNIMEではECFP4をどうやって算出するの?」と聞いて「Morganで半径2に設定してください」と言われて「??」となったことがあるので以下引用しておきます。
circularフィンガープリントとしてより知られているかもしれませんが、 Morganフィンガープリントと呼ばれる一連のフィンガープリントは、ユーザー定義のアトム不変量のセットに対してMorganアルゴリズムを適用することで生成されます。 Morganフィンガープリントを生成するときには、フィンガープリントの半径を定義しなければなりません
RDKitで生成したECFP/FCFPフィンガープリントとMorganフィンガープリントを比較する際には、Morganフィンガープリントのパラメーターが半径であるのに対して、 ECFP4の4は考慮している原子の環境の直径に一致していることを思い出してください。」
よってMorganフィンガープリントを生成するときに
「半径=2とすることで、ECFP4とFCFP4とおおよそ等価となります。
【RDKit Fingerprint】
日本語化されたノードディスクリプションによると、このノードは
入力された RDKit Mol カラムのハッシュ化されたビットベースのフィンガープリントを生成し、テーブルに追加します。
ハッシュ化されたビットベースのフィンガープリント
についてはひとまず「化学の新しいカタチ」より引用させていただきます。
データにある処理を施すことで,長さ一定(1024や2048が多いです)のビット配列に0か1を埋め込んだ形式に変換を行うことが多いです.この作業のことをハッシュ化と呼びます.
では「ある処理」とは?となるでしょうが、私は深入りできるほど理解できていないので下記記事の紹介に留めます。
設定:
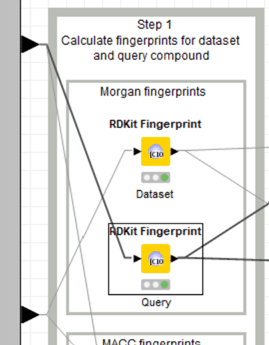
フローが交差しているのでちょっとわかりにくいですね。
A) QueryすなわちGefitinib (下のノード)
B) DatasetすなわちW2の出力である4510化合物 (上のノード)
設定内容は揃えてあるのでA)のQueryの方だけお示しします
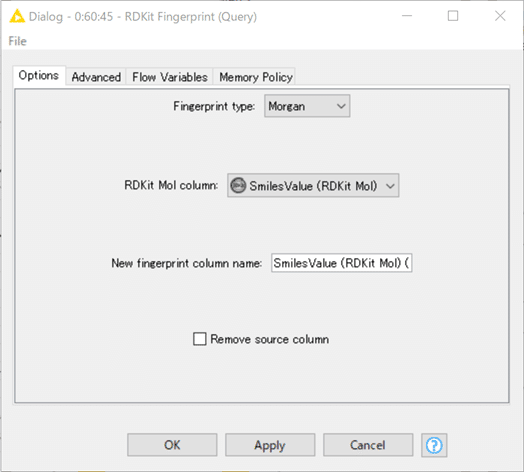
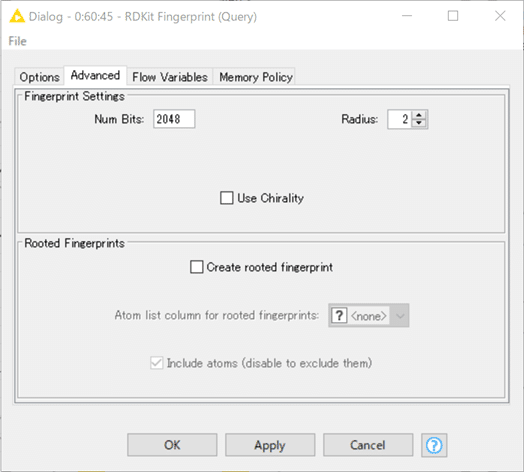
ビット長2048のMorgan2(すなわちECFP4相当)を算出します。
結果:
A) Query

B) Dataset
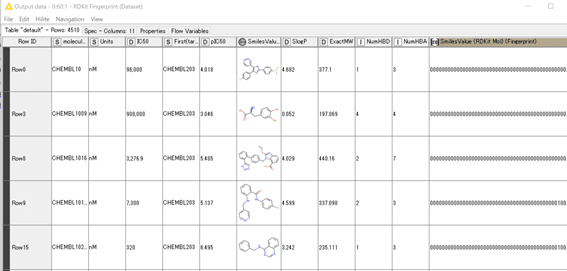
以上となります。
次はStep1の下部、MACCSフィンガープリントの算出へ進めます。
心底おまけ:
【修羅場すぎる】
0,1のビットとはいえ、先述の結果は0が多いなあと感じませんか。
あまりにも0の率が高いと疎(スパース)なデータになってしまうわけです。
少~しだけ関連する個人的に好きな記事を紹介しておきます。
いいなと思ったら応援しよう!

