豆を落として円の面積を求める！（モンテカルロ法）

みなさん円の面積はどうやって求めますか？学校で習ったのは

「半径×半径×3.14」とか、「πr^2(二乗）」とかだと思います。

もう少し面白い面積の求め方を知っていますでしょうか。

その名も「モンテカルロ法」。

簡単に説明すると、円を書いた正方形の紙の上に豆を落とすことを繰り返し、円内に入った豆の数を数えて試行回数で割り算することで、円の面積を求めようというものです。

「は？」

って感じですよね。

縦1、横1の正方形の紙の上に書いた半径1の円を四等分した四分円を想像してください。円の上に豆が乗っかる確率はどれくらいでしょうか。これは直感的に円の面積の大きさと同じだとわかると思います。この確率を求めようというのがモンテカルロ法です。

もちろん、5回や10回では、正しい数値からは大きく外れた結果になります。これはサイコロの出る目がそれぞれ1/6であることと同じですね。試行回数が少なければ理論値からの外れ度合いも大きくなります。

先に正解をお伝えしておきましょう。半径1の四分円の面積はいくつかというと、

　面積＝1（半径）×1（半径）×3.14 / 4 =0.785

です！

では今回は10回、100回、1000回、10000回豆を落とし続けたとして結果を見て見ましょう。この回数を手で豆を落とすのは気が狂いそうなので、パソコンに計算してもらいました。（コードが気になる方は一番後ろに載せておきます。）

●10回豆を落とした場合

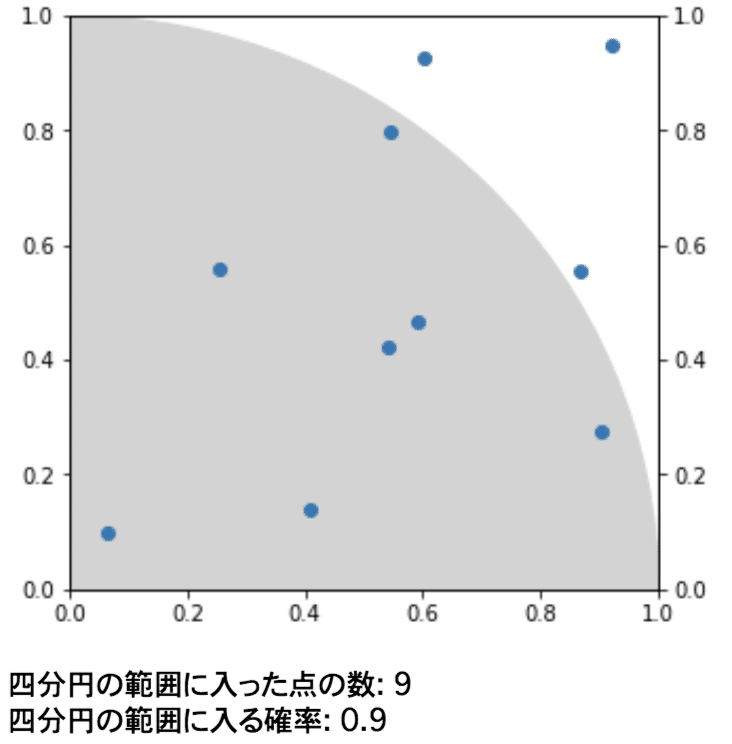
おー確率は0.9でした！0.785からは大きく外れていますね。

●100回豆を落とした場合

お、ついに少数第一位が0.7で正解と一致しました！が、まだ0.785とは誤差があります。

●1000回豆を落とした場合

だいぶ近づいてきました！正解からは0.14の誤差です！

では最後に10000回やってみましょう！

●10000回豆を落とした場合

ついに！正解の0.785とほぼ一致する値となりました！

公式だけで覚えている数学よりもちょっとだけ魔法のようで、面白いですよね！

●参考情報：

いかに今回使ったpythonのコードを載せておきます。

# Figureを作成
fig = plt.figure(figsize=(5, 5))

# FigureにAxes(サブプロット)を追加
ax = fig.add_subplot(111)

# matplotlib.patches.Circleのインスタンスを作成
# 中心位置の座標は左下を基準に全体の幅を1として設定
# radiusは半径、colorは塗り潰しの色
c = pat.Circle(xy = (0, 0), radius = 1, color = "lightgray")

# Axesに円cを追加
ax.add_patch(c)

#X軸を共通とする。
ax2 = ax.twinx()

#試行回数が10000回の場合のランダムな[0-1]の値を生成
X = rand(10000)
Y = rand(10000)
plt.xlim(0, 1)
plt.ylim(0, 1)
#２つめのグラフ
ln2=ax2.scatter(X,Y)
plt.show()
count = 0
for i in range(len(X)):
   #円の方程式（X^2 + Y^2 = 1）の内側に含まれる点を判別
   Z = X[i]** 2 + Y[i]** 2
   if Z <= 1:
       count += 1
   else:
       continue
print("四分円の範囲に入った点の数: " + str(count))
print("四分円の範囲に入る確率: " + str(count/len(X)))