ONE PIECEカードゲームにおけるデッキ採用枚数の確率の話
どうもKJです。
最近デッキビルダーとしていろんな(変な)デッキを作ってます。
カタクリの記事が大変好評を頂いており、様々な質問を受けるようになりました。
TwitterDMで質問受けてるので、遠慮なくご連絡ください。
さて、今回は確率の話をします。
一応理系出身で大学院まで化学の専攻でしたが、数学が得意でした。(昔から計算ミスを大事なところでしてしまい、今でも対戦中の計算ミスをしてますが)
なので、大学院を修了してかれこれ10年近く経ちますが、簡単な計算はまだまだやり方がわかるのと数的感覚があるので、カードゲームでも役立ってはいます。
今回の記事は、「確率なんて計算難しい。わかんない。」「デッキ組んだけどなんか安定して上手く回らないなー」といった方向けに、実は複雑な計算は無しでカードゲームの確率計算が出来ることを伝えたいと思います。
普通の電卓で計算できますが、関数電卓アプリを使うと計算式を確認しながら出来るのでより簡単ですので、関数電卓アプリを使用されることを推奨します。
応用編は複雑な計算が必要なのでシンプル計算の方法も記載してます。
基本編の計算にも使える簡易計算方法でもあるので、最後まで読んでいただけたら幸いです。
ちなみに一応わかりやすく書いてるつもりですが、何言ってるのかわからん!ってなったりしたら改善していきたいので、不明点等も含めて、遠慮なくTwitterDMでご連絡ください。
確率計算方法
まずは、計算方法の説明から。
あるカードを引きたいときに1枚以上来る確率を計算するのが基本です。
2枚来てほしいとかは複雑になるので、1枚以上引く確率を出すのが一番簡単に計算できます。
なぜなら「1枚以上を引く=全体から全く引かない確率を引いた確率」だからです。

中学生くらいに集合という概念を数学で習ったと思います。
全体から全く引かない部分以外は1枚以上引けるで構成されます。
(図1参照)
つまり、計算方法は「100% - 全く引かない確率」を計算すれば1枚以上引く確率が出ます。
では、全く引かない確率をどう出すかを計算します。
例題 サーチ1種類を引く確率
いろんなデッキで使える計算です。
例えば黄色の単色デッキはサーチはプリンしかいません。
プリンを4枚採用した場合、プリンを初手に引く確率を計算してみます。
まずは、前述の通り、プリンを1枚も引かない確率を出します。
初手の手札は5枚。
1枚ずつめくっていくとすると、初手1枚目にプリンが来ない確率は、プリン以外のカードを引く確率なので、50-4をした46枚、デッキ50枚から46枚を引けばいいので、確率は46/50です。
2枚目は、1枚目で捲ったカード分減るので、プリン以外のカードは45枚でデッキ枚数は49枚になります。すなわち45/49です。
3枚目は同じ考えをして44/48、4枚目は43/47、5枚目は42/46となります。
これらが組み合わさった際の確率なので全部掛け算してあげます。
つまり試行回数分だけ分子と分母の数を減らしていき、それらを掛け合わせればいいということです。
46/50×45/49×44/48×43/47×42/46≒0.64696
0.64696×100≒64.7%
(%表記は100倍すればOKなので以下は数式に100をかけてます)
つまり、サーチプリンを初手で引かない確率は64.7%、引く確率は逆の部分なので、100%-64.7%=35.3%となります。
つまり3試合に1回位しか引かないんですね。
4枚積んでるカードは初手に来る確率は3試合に1回程度。
これが基本です。
この計算をいろんなパターンですることで、様々な確率を出せます。
採用枚数と初手に来る確率(基本編)
まずは、一番基本の初手に来る確率の計算。
例題でサーチ1種4枚の場合を計算しました。
同じ計算方法で3枚の時を計算してみましょう。
3枚採用のカードの初手率
3枚以外ということで47枚のカードを引く確率を計算します。
47/50×46/49×45/48×44/47×43/46×100≒72.4%
つまり、3枚採用のカードが来る確率は27.6%。
およそ4試合に1回。
この計算をすると、サーチカードは4枚積むことが最低ラインなのがわかりますね。
3試合に1回と4試合に1回だと全然違いますね。
マリガンは1回までなので期待値は感覚的には4枚採用だとマリガン込みでも5試合に3試合くらい引けますが、3枚だと5試合に2試合くらいになります。
サーチ2種の場合
サーチが4枚採用した方が良いのが理論的にわかった上で、じゃあ2種のサーチを採用してる場合を考えます。
2種8枚なので、引かない確率は42/50から同じように計算します。
42/50×41/49×40/48×39/47×38/46×100≒40.1%
つまり、サーチを引ける確率は59.9%となります。
50%を超えてるので期待値的にはマリガン込みでおおよそ毎試合1枚は引ける確率が高いということになります。
ドロー込みでの確率(ちょい応用編)
先攻2ターン目で出したいキャラがいるとします。(主に3コスキャラとします)
その時は初手に+1ドロー分が加わります。
その時も同じ方法で計算ができます。
初手サーチとかはしていない前提の確率なので、サーチしたらさらに確率が上がりますが、サーチで持って来たいカードは様々かと思いますので、無視してます。サーチでさらに安定しやすくなると思って以下は読んでください。
先攻2ターン目3コスキャラを引く確率
1ドロー分追加になるので、先程の計算に試行回数を1回追加すればOKです。
仮に1種4枚であった場合は4枚採用なので、46/50から始めて6枚ドローで計算すればOKです。
(先攻2ターン目として記載してますが、確率上は1ドロー分込みなので後攻1ターン目の初手確率と同じになります)
46/50×45/49×44/48×43/47×42/46×41/45×100≒58.9%
つまり、1ドロー込みでの確率は41.1%となります。
マリガン込み期待値でも感覚的には3試合に1回は来なそうですね。
仮に2種8枚なら?
42/50×41/49×40/48×39/47×38/46×37/45×100≒33.0%
つまり、67.0%程になります。
序盤の動きを高めたいならこの位の確率があればマリガン込みでの期待値的に安定しそうですね。
3コスキャラを合計5枚、6枚、7枚の例も出しておきましょう。
5枚の場合
45/50×44/49×43/48×42/47×41/46×40/45×100≒51.3%
引く確率は48.7%
期待値的にマリガン込みでちょっと引けそう。
3-4試合に1回位は来ない気がしますね。
6枚の場合
44/50×43/49×42/48×41/47×40/46×39/45×100≒44.4%
引く確率は55.6%
期待値的にマリガン込みでそこそこ引けそう
4-5試合に1回位は来ない気がします。
7枚の場合
43/50×42/49×41/48×40/47×39/46×38/45×100≒38.4%
引く確率は61.6%
期待値的にマリガン込みでまぁまぁ引けそうです。
このくらいなら安定しそうです。
現実的に試合展開をどういうデッキにするかですが、とにかくドンの枚数に合わせたキャラを並べたい場合は3コス帯は6枚以上入れるとそこそこ下ブレなさそうな確率になります。
黄カタクリや赤ルフィだとペローやスターターゾロを並べたいところの確率になりますので、4枚だと安定しないのであと1-2枚は最低でも3コス帯を入れた方が序盤が腐りにくいです。
赤ルフィなら速攻ゾロやロビンなどを採用していけば安定、黄カタクリならバニラのペコムズを1-2枚追加するだけで安定度が上がります。
赤緑ロー、赤緑ルフィなら2ターン目もサーチで問題ないので、サーチを増やす方が安定しますね。
先攻3ターン目4-5コス帯の引く確率
今回は2ドローです。
計算方法は先程までと同じで試行回数が1個増えた場合なので、早速計算に入ります。
4枚の場合46/50×45/49×44/48×43/47×42/46×41/45×40/44×100≒53.6%
引く確率は46.4%
期待値的にマリガン込みでちょっと引けそう。
3-4試合に1回位は来ない気がしますね。
5枚の場合45/50×44/49×43/48×42/47×41/46×40/45×39/44×100≒45.4%
引く確率は54.6%
期待値的にマリガン込みでそこそこ引けそう。
4-5試合に1回位は来ない気がしますね。
6枚の場合44/50×43/49×42/48×41/47×40/46×39/45×38/44×100≒38.4%
引く確率は61.6%
期待値的にマリガン込みでまぁまぁ引けそう
このくらいなら安定しそうです。
つまり、先攻3ターン目に出したいキャラは5-6枚あれば確率的には十分そうです。
赤ルフィなら5マルコ+αで4-5コス帯を入れておく。
黄カタクリなら今流行り始めてる4/6000バニラは5-6体で十分ということ。
赤緑ローでも5コス帯を自引きする確率は5-6枚以上で安定するということ。
サーチの確率(応用編1)
さてここから少しだけ計算が複雑になります。
ただそれをやるのはすごく大変なので、正確には間違ってるけどシンプル計算に変えて、おおよその確率を出す計算方法を紹介します。
実際は引くか引かないかの運要素なので細かい計算値より概算計算で十分ですので、概算計算も紹介します。
サーチの確率はとても大事です。
採用枚数によって事故率が大きく変わります。
特に2種以上のサーチを入れてたり、サーチ対象じゃないカードが多く採用されてる場合は特に気を付けなければなりません。
ここでは例のレシピを2パターン使って計算しますので、実際にどのくらいのサーチ確率になるかは、自分のデッキできちんと計算してみてください。
サーチ計算例(赤緑ロー)

例題用の赤緑ローの構築で計算してみましょう。
まず、サーチ対象の枚数を数えます。
ナミ:14枚
ダダン:20枚
ボニー:20枚(ボニーも対象なので)
単純に考えるとサーチを対象を引く確率は先程までと同様を引かない確率を求めればOKです。
初手にサーチするなら45枚の内、手札(ハンド)に対象がいるかいないか、その枚数は・・・って計算難しすぎます!
構築考えてるときにそんな計算できない!!
なので間違ってるけど概算で出します。
ナミの場合はサーチ対象以外は36枚で5枚捲るので、デッキ全体でどのくらい5回捲ってサーチ対象がいるかの計算で出してみます。
つまり、先程までの計算と同じように計算してみます。
36/50×35/49×34/48×33/47×32/46×100≒17.8%
1枚以上引く確率は82.2%
同じようにダダンとボニーは20枚で5枚捲るとすると、
30/50×29/49×28/48×22/47×21/46×100≒6.7%
1枚以上捲る確率は93.3%
つまりこのデッキだとほぼほぼサーチをスカらないと思われます。
さらにざっくり計算するならナミは36/50を5回繰り返す、ダダンとボニーは30/50を5回繰り返すので、
(36/50)の5乗×100≒19.3%
1枚以上引く確率は80.7%
(30/50)の5乗×100≒7.8%
1枚以上引く確率は92.2%
この計算でも割と近い値になります。
超ざっくり計算するなら枚数比を試行回数分掛けても(累乗しても)概算は出せるということですね!
実際のサーチはこの確率を踏まえて、今出てるカードや手札にあるカードの枚数が例えばナミの対象が多ければ、ナミのサーチ確率は下がり、ボニーの確率は上がる、逆にボニーのサーチ対象が多ければボニーの確率は下がって、ナミのサーチ確率は上がります。
サーチの順番はこれを意識するといいですね!
この計算結果から言えることは、このような構築の場合は初手にナミのサーチをした際にはおおよそ5回に1回はスカる可能性があります。
つまり、後攻を選択してダダンのサーチから入った方がサーチ上は安定しやすいということです。
前述の通り、ハンドに来てるカードによって確率は大きく変わりますのであくまで目安計算として今のようなことがわかるので、サーチ計算は一度しておいた方がいいですね!
ライフのトリガー確率(応用編2)
主に黄色のデッキ向けの確率です。
トリガージェッピやトリガーギブソンの確率も計算は出来ますが、初手に来る確率の計算と同じなので、計算過程は割愛しますが、4枚採用しててライフ5枚なら最初のサーチプリンが来る確率と同じなので、3試合に1回位はトリガージェッピできます。
(ジェッピ4枚採用していることはないと思いますが)
エースデッキなら炎帝、ジェッピ、火拳のトリガー率はかなり高くなってきますね。
合計8枚入れてたらサーチ2種が初手に来る確率と同じなので、3試合に2回くらいはトリガーを使えるチャンスがあります。
それが一番上か、一番下かはわからないので、あくまで確率論なだけです。
さて、黄色のデッキはライフ回復やダイフクによりライフ交換が出来ます。
これらによりおおよそ7ライフ分くらいは1試合にあると思います。
そこでトリガー付きキャラを採用した枚数とトリガー期待値を計算します。
例えばトリガー20枚採用の場合
20/50がトリガーです。
7ライフに来る確率はシンプルに計算すると
7×20/50=2.8枚
つまり約3枚トリガー発動するということ。
15枚採用の場合は
7×15/20=2.1枚
つまりライフ回復や入れ替えした上でも2回しかトリガーが発動しません。
ちなみに下記の場合の結果だけ並べます。
16枚:2.24枚
17枚:2.38枚
18枚:2.52枚
19枚:2.66枚
ちなみにライフ回復なくて5ライフで計算すると
15枚:1.5枚
16枚:1.6枚
17枚:1.7枚
18枚:1.8枚
19枚:1.9枚
20枚:2枚
6ライフで計算すると
15枚:1.8枚
16枚:1.92枚
17枚:2.04枚
18枚:2.16枚
19枚:2.28枚
20枚:2.4枚
これらの確率を加味すると17枚以上は最低でもトリガー採用した方が安定して2枚程度のトリガー発動が出来る計算となります。
個人的には2ライフ回復時に3枚トリガー発動できた方がいいと考えてるので最低ラインは18枚です。
ここで2回のトリガーに何が来るかも確率を出します。
例として18枚トリガー採用してる内の4枚採用が来る確率です。
計算方法はこれまでと同じで4枚採用が来ない確率を引いてあげれば出ますので、
14/18×13/17×100≒59.5%
つまり4枚採用してるカードがトリガーの確率は40.5%
同じように3枚、2枚、1枚も計算します。
3枚:31.4%
2枚:21.6%
1枚:11.1%
トリガー18枚採用してて、その内4枚採用してても4割くらいの確率しかありません。
トリガーの母数が増えて20枚になれば、確率は更に下がります。
トリガーに来てほしいカードはたぶん雷霆、アタッカー、威国が優先度が高いと思います。
自ずと何を何枚採用すべきかが見えてきますね。
しらほしは素出しは基本1ターン損するのでしないとしたら、雷霆よりも来てほしいでしょうか?
トリガー登場のアタッカーより来てほしいでしょうか?
自分のデッキの優先度を考えて枚数比を考えましょう。
しらほしは採用しても個人的にはピン刺しか2枚までで期待値的にも充分だと思います。
(カタクリの記事にも同様なことを書いてますが)
それより雷霆欲しいんじゃないですかね?
トリガー登場アタッカー出したいんじゃないですかね?
よりトリガー確率を上げたいカードは何なのかを考えて構築してみましょう!
計算するとそれが見えてきます。
終わりに
試合数を重ねれば確率収束してくるので、今組んでるデッキで似たような計算をしてみると、確かにそのくらいでスカったりしてたなーと感じると思います。
5試合に1回起こるということはスタバ32人開催で1回は起きるということです。
どこかで1試合事故るなーって思う人は計算をしてみてください。
たぶん計算結果も同じくらいの確率になってると思います。
まぁ個人的には5試合に1回の事故率なら上振れれば5試合安定する場合もあるので、割りとアリなラインとは考えてます。
より安定したい人は計算上6試合に1回くらい事故るような構築を目指してもいいと思います。
デッキを組む際に計算をしておけば試運転する前に何となくは、安定性がわかるのでここまで読んだ方は一度計算を!
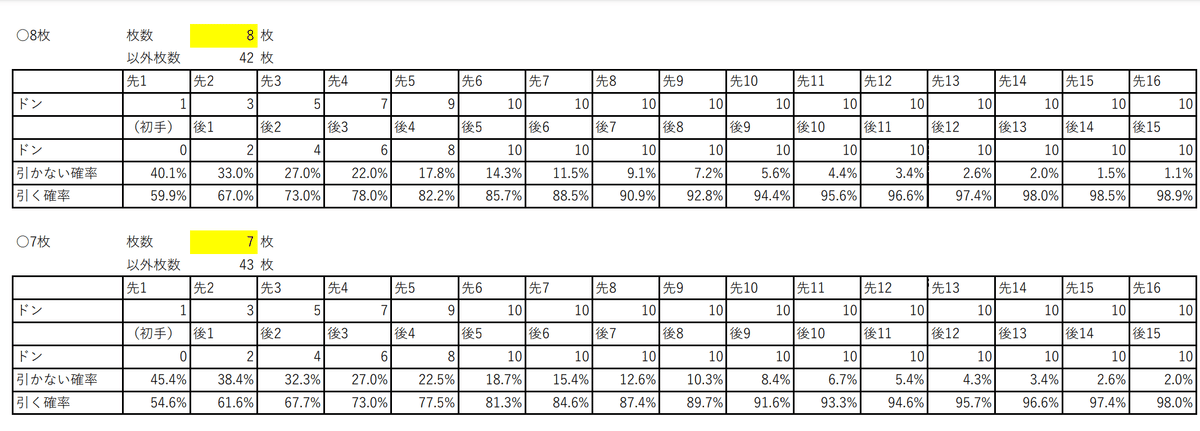
確率早見表(2023/6/14追記)
採用枚数毎の確率早見表を作ったのでアップします。
8枚からにしてるのは同じ役割のカード2種4枚採用の想定ですので、目安にしてください。



この記事が気に入ったらサポートをしてみませんか?
