
Pythonライブラリ(ベイズ統計モデル):PyMC3
1.概要
ベイズ統計モデルのPyMC3を紹介します。PyMC3の特徴として「ハミルトニアンモンテカルロ(HMC; Duane, 1987)の自己調整型変種であるNo-U-Turn Sampler (NUTS; Hoffman, 2014) などの次世代マルコフ連鎖モンテカルロ(MCMC)サンプリングアルゴリズム」があります。


なお2022年6月の段階でPyMC(4.0に相当)へ移行しており、バックエンドも「Theano(数値計算ライブラリ※開発終了)」から「aesara」に移行しております。
まず情報量の多いPyMC3で学習後にPyMC4を学習したいと思います。

1-1.ベイズ統計モデルとは
ベイズ統計学では未知の量(未知のパラメータや将来の観測値など)に対する不確実性を確率で表現し、これをモデル化したものがベイズ統計モデルです。これによりパラメータの推定や予測問題などに適用できます。
1-2.環境構築
私の環境(Windows10, Anaconda)では「pip install pymc3」だけで動きました。公式Docsでは下図の通りOSごとの説明があり、かつ仮想環境を推奨しておりますのでエラーが出た方は公式Docsをご確認ください。

[Terminal]
pip install pymc3【ArviZに関して】
ArviZはベイズモデルの探索分析用パッケージであり、PyMC3のバックエンドでも動いています。Anacondaユーザーなら自動でインストールされると思いますが、インポートエラーが出る場合は追加が必要です。
[Terminal]
pip install arviz【エラー時の対応】
下記記事では「PyMC3 の依存するパッケージ Theano は、Python 3.4 以上 3.6 未満で動作」と記載があるため、特定の条件ではエラーが出る可能性があります。
1-3.Quick Start
まずは公式のトップにあるコードで動作確認しました。"X, y = linear_training_data()"は自分で設定する必要があるためsklearnのdatasetsから回帰の「Boston datasets」を使用しました。

サンプルコードのポイントは下記の通りです。
参照コードは1次元配列(特徴量が1個)用のため、1次元で抽出
全データ(506個)だと1時間以上でも終わらないため10個だけ抽出(10個の場合は1.5min程度で終了)
[IN]
import pymc3 as pm
boston = datasets.load_boston()
df_X = pd.DataFrame(boston.data, columns=boston.feature_names)
df_y = pd.DataFrame(boston.target, columns=['target'])
X = df_X[['TAX']].values #説明変数:住宅税率
y = df_y['target'].values #目的変数:住宅価格
#データ数を10個に絞る
X,y = X[:10], y[:10]
print(f'データ形状 X: {X.shape}, y: {y.shape}')
with pm.Model() as linear_model:
weights = pm.Normal("weights", mu=0, sigma=1) #重み:正規分布
noise = pm.Gamma("noise", alpha=2, beta=1) #ノイズ:ガンマ分布
y_observed = pm.Normal(
"y_observed",
mu=X @ weights,
sigma=noise,
observed=y,
)
prior = pm.sample_prior_predictive() #事前分布からサンプリング
posterior = pm.sample() #事後分布からサンプリング
posterior_pred = pm.sample_posterior_predictive(posterior) #事後予測分布からサンプリング[OUT]
データ形状 X: (10, 1), y: (10,)
c:\Users\KIYO\Anaconda3\lib\site-packages\deprecat\classic.py:215: FutureWarning: In v4.0, pm.sample will return an `arviz.InferenceData` object instead of a `MultiTrace` by default. You can pass return_inferencedata=True or return_inferencedata=False to be safe and silence this warning.
return wrapped_(*args_, **kwargs_)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Initializing NUTS using jitter+adapt_diag...
c:\Users\KIYO\Anaconda3\lib\site-packages\theano\tensor\elemwise.py:826: RuntimeWarning: divide by zero encountered in log
variables = ufunc(*ufunc_args, **ufunc_kwargs)
c:\Users\KIYO\Anaconda3\lib\site-packages\theano\tensor\elemwise.py:826: RuntimeWarning: invalid value encountered in multiply
variables = ufunc(*ufunc_args, **ufunc_kwargs)
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [noise, weights]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 82 seconds.結果として事後分布による推定結果が得られました。
[IN]
print(posterior_pred.keys())
print(posterior_pred['y_observed'].shape)
[OUT]
dict_keys(['y_observed'])
(4000, 10, 10)1-4.ライブラリの読み込み
PyMC3を”import pymc3 as pm”で読み込みます。またPyMC3で使用するArvizも合わせて"import arviz as az"で読み込みました。
その他ライブラリと説明用のための自作関数も用意しました。
[IN]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib
import arviz as az
import pymc3 as pm
from sklearn import datasets
class HorizontalDisplay:
def __init__(self, *args):
self.args = args
def _repr_html_(self):
template = '<div style="float: left; padding: 10px;">{0}</div>'
return "\n".join(template.format(arg._repr_html_())
for arg in self.args)2.モデル作成
PyMC3のモデルオブジェクトの使用方法を説明します。
2-1.PyMC3の概要
詳細説明の前に簡単なPyMC3の概要を説明します。ベイズの定理は下記式となります。
$$
P(\theta | D) = \frac{P(D | \theta) P(\theta)}{P(D)}
$$
$${P(\theta | D)}$$ :事後分布 (Posterior) であり、データ $${D}$$ が与えられたときのパラメータ $${\theta}$$ の確率分布を表します。
$${P(D | \theta)}$$ :尤度 (Likelihood) であり、パラメータ $${\theta}$$ が与えられたときのデータ $${D}$$ の確率を表します。
$${P(\theta)}$$ :事前分布 (Prior) であり、データ $${D}$$ を観測する前のパラメータ $${\theta}$$ の確率分布を表します。
$${P(D)}$$ :データ $${D}$$ の確率であり、全ての可能な $${\theta}$$ についての $${P(D | \theta) P(\theta)}$$ の積分または和として得られます。これは、事後分布を確率分布として正規化するために用いられます。
ここでPyMC3でこれらを次のように実装します。なお正規化項$${P(D)}$$はMCMCを使用するため定義は不要です。
事前分布:pymc3で定義された確率分布
尤度:事前分布を引数として渡された分布
事後分布:事前分布と尤度が自動判定されるため”pm.sample()”のみでMCMCにより事後分布が取得できる

2-2.モデルの定義方法:with pm.Model()
PyMC3ではModelクラスを使用してwith構文でモデルを定義します。下記の通りwith構文で定義した変数は"<class 'pymc3.model.Model'>"型であり各種メソッド・属性を持ちます。
[IN]
with pm.Model() as model:
pass
print(type(model))
for i in dir(model):
if not i.startswith("_") and not i.endswith("_"):
print(i)[OUT]
type: <class 'pymc3.model.Model'>
RV_dims
Var
add_coords
add_random_variable
basic_RVs
bijection
check_bounds
check_test_point
cont_vars
contexts
coords
d2logp
d2logp_nojac
datalogpt
deterministics
dict_to_array
disc_vars
dlogp
dlogp_array
dlogp_nojac
fastd2logp
fastd2logp_nojac
fastdlogp
fastdlogp_nojac
fastfn
fastlogp
fastlogp_nojac
flatten
fn
free_RVs
isroot
logp
logp_array
logp_dlogp_function
logp_elemwise
logp_nojac
logp_nojact
logpt
makefn
missing_values
model
name
name_for
name_of
named_vars
ndim
observed_RVs
parent
potentials
prefix
profile
root
shape_from_dims
test_point
unobserved_RVs
varlogpt
vars今は変数を定義しただけのためオブジェクトに情報はありません。
[IN]
with pm.Model() as model:
pass
print(f'basic_RV: {model.basic_RVs}')
print(f'free_RV: {model.free_RVs}')
print(f'observed_RV: {model.observed_RVs}')
print(f'logp: {model.logp}')[OUT]
basic_RV: []
free_RV: []
observed_RV: []
logp: <pymc3.model.LoosePointFunc object at 0x000001B78D532B50>2-3.統計モデルの定義
統計モデルを定義するには"with pm.Model() as model"のブロック内に定義するモデルを記載します。下記では正規分布を記載しました。
モデルだけでなく定義した変数xにもPyMC3の型が付きました。
[IN]
with pm.Model() as model:
x = pm.Normal('x', mu=0, sigma=1)
print(f'データ型 model: {type(model)}, x: {type(x)}')
print(f'basic_RV: {model.basic_RVs}, free_RV: {model.free_RVs}, observed_RV: {model.observed_RVs}, logp: {model.logp}')[OUT]
データ型 model: <class 'pymc3.model.Model'>, x: <class 'pymc3.model.FreeRV'>
basic_RV: [x ~ Normal]
free_RV: [x ~ Normal]
observed_RV: []
logp: <pymc3.model.LoosePointFunc object at 0x000002AD12AE2B20>2-4.分布からのサンプリング:pm.sample()
PyMC3では得られた分布(特に重要なのは事後分布)からサンプリングするために"pm.sample()"を使用します。
[API]
pymc.sample(draws=1000, *, tune=1000, chains=None, cores=None,
random_seed=None, progressbar=True, step=None,
nuts_sampler='pymc', initvals=None, init='auto',
jitter_max_retries=10, n_init=200000, trace=None,
discard_tuned_samples=True, compute_convergence_checks=True,
keep_warning_stat=False, return_inferencedata=True,
idata_kwargs=None, nuts_sampler_kwargs=None, callback=None,
mp_ctx=None, model=None, **kwargs) 2-4-1.基礎的な使い方
サンプルとして標準正規分布から1000個サンプリングします。記法は一般的に"trace=pm.sample()"とします。
[IN]
with pm.Model() as model:
x = pm.Normal('x', mu=0, sigma=1)
trace = pm.sample(1000, chains=1)
print(f'trace: {type(trace)}')
trace[OUT]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Initializing NUTS using jitter+adapt_diag...
Sampling 1 chain for 1_000 tune and 1_000 draw iterations (1_000 + 1_000 draws total) took 2 seconds.
Only one chain was sampled, this makes it impossible to run some convergence checks
trace: <class 'pymc3.backends.base.MultiTrace'>
<MultiTrace: 1 chains, 1000 iterations, 1 variables>traceのデータ型は"<class 'pymc3.backends.base.MultiTrace'>"であり、複数の属性が割り当てられています。
[IN]
for i in dir(trace):
if not i.startswith("_") and not i.endswith("_"):
print(i)[OUT]
add_values
chains
get_sampler_stats
get_values
nchains
point
points
remove_values
report
stat_names
varnamesサンプリングデータは”trace[<定義した変数>]”でNumpy配列としてデータ抽出が可能です。
[IN]
trace['x'] #trace.x でもOK[OUT]
array([ 5.04443090e-01, 4.14840584e-01, 1.04230175e+00, 1.06756190e+00,
-2.63899836e-01, 2.37732892e+00, -2.23186328e+00, -1.79066003e+00,
-1.79066003e+00, 2.06743588e+00, 7.98002789e-01, 2.78964417e-01,
4.06769387e-01, 3.65267211e-01, 6.89100680e-01, -4.86540258e-01,・・・])データを確認すると正規分布になっていることが確認できます。
[IN]
x_sample = trace.x
sns.histplot(x_sample, kde=True)
[OUT]
2-4-2.推論値:return_inferencedata
推論値も合わせて出力する場合は”return_inferencedata=True”を設定します。Model()でサンプリング後にtraceを呼び出すとクリックできる画面が出現(今回は"posterior"と"sample_stats")し、様々な情報が含まれます。
データ型は"<class 'arviz.data.inference_data.InferenceData'>"となり、使用できる属性などが変わることに注意が必要です。
[IN]
with pm.Model() as model:
x = pm.Normal('x', mu=0, sigma=1)
trace = pm.sample(1000, chains=1, return_inferencedata=True)
print(type(trace))
trace
[OUT]
class 'arviz.data.inference_data.InferenceData'>


2-4-2.Dfへ変換:pm.trace_to_dataframe
得られたサンプリング結果をPandasのDataFrame型へ変換するには"pm.trace_to_dataframe()"を使用します。
[IN]
pm.trace_to_dataframe(trace)
[OUT]
3.基礎API:PyMC3/ArviZ
PyMC3での基礎的なAPIを紹介します。APIは”PyMC3”と”ArviZ”の2種類ありますがどちらを使用しても特に問題はないと思います。
サンプルデータとしてchain数=3の標準正規分布を使用しました。
[IN]
import arviz as az
import pymc3 as pm
with pm.Model() as model:
x = pm.Normal('x', mu=0, sigma=1)
trace = pm.sample(1000, chains=3)[OUT]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (3 chains in 4 jobs)
NUTS: [x]
Sampling 3 chains for 1_000 tune and 1_000 draw iterations (3_000 + 3_000 draws total) took 15 seconds.3-1.統計(Stats)
統計データに関するAPIを紹介します。
3-1ー1.サマリー:az.summary()
サンプリング結果のサマリー確認はArviZのsummary()、またはPyMC3の"pm.summary()"を使用します。APIと一部の出力結果に関しても記載しました。
[API]
arviz.summary(data, var_names=None, filter_vars=None, group=None,
fmt='wide', kind='all', round_to=None, circ_var_names=None,
stat_focus='mean', stat_funcs=None, extend=True,
hdi_prob=None, skipna=False, labeller=None,
coords=None, index_origin=None, order=None)【出力】
loo:Pareto-smoothed importance sampling leave-one-out cross-validation (PSIS-LOO-CV)
ess:有効サンプルサイズの推定値
rhat:traceのランク正規化splitR-hatの推定値
mcse:マルコフ連鎖標準誤差の統計量
結果は下記の通りです。
[IN]
az.summary(trace, var_names=['x']).T
# pm.summary(trace, var_names=['x'])
[OUT]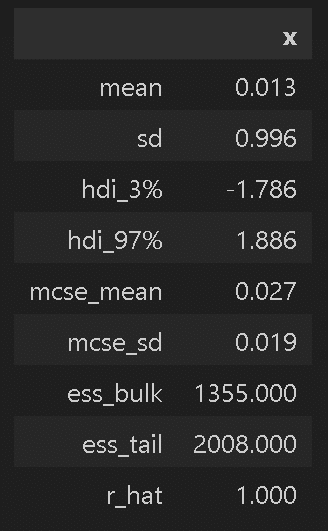
3-2.プロット(Plots)
可視化に関するAPIを紹介します。
3-2-1.トレースプロット:pm.traceplot()
分布のプロットは"pm.traceplot()"で実装できます。またArvizベースだと"pm.plot_trace()"でも実装可能です。
[API]
pymc3.plots.traceplot(trace, varnames=None, transform=<function identity_transform>,
figsize=None, lines=None, combined=False, plot_transformed=False,
grid=False, alpha=0.35, priors=None, prior_alpha=1,
prior_style='--', ax=None, live_plot=False, skip_first=0,
refresh_every=100, roll_over=1000)[API]
arviz.plot_trace(data: arviz.data.inference_data.InferenceData,
var_names: Optional[Sequence[str]] = None, filter_vars: Optional[str] = None,
transform: Optional[Callable] = None,
coords: Optional[Dict[str, List[Any]]] = None,
divergences: Optional[str] = 'auto',
kind: Optional[str] = 'trace', figsize: Optional[Tuple[float, float]] = None,
rug: bool = False, lines: Optional[List[Tuple[str, Dict[str, List[Any]], Any]]] = None,
circ_var_names: Optional[List[str]] = None, circ_var_units: str = 'radians',
compact: bool = True, compact_prop: Optional[Union[str, Mapping[str, Any]]] = None,
combined: bool = False, chain_prop: Optional[Union[str, Mapping[str, Any]]] = None,
legend: bool = False, plot_kwargs: Optional[Dict[str, Any]] = None,
fill_kwargs: Optional[Dict[str, Any]] = None, rug_kwargs: Optional[Dict[str, Any]] = None,
hist_kwargs: Optional[Dict[str, Any]] = None, trace_kwargs: Optional[Dict[str, Any]] = None,
rank_kwargs: Optional[Dict[str, Any]] = None, labeller=None, axes=None,
backend: Optional[str] = None, backend_config: Optional[Dict[str, Any]] = None,
backend_kwargs: Optional[Dict[str, Any]] = None, show: Optional[bool] = None)結果をプロットすると3本の正規分布とサンプリング数に関するプロットが確認できます。
[IN]
pm.traceplot(trace, var_names=['x'])
# pm.plot_trace(trace, var_names=['x'])
[OUT]
3-2-2.フォレストプロット:az.plot_forest()
フォレストプロットとはメタ分析の結果を図に表したもので,複数の研究結果とそれらを統合した結果を視覚的に確認することができます。
PyMC3では"arviz.plot_forest()"で実装できます。
[IN]
az.plot_forest(trace, var_names=['x'])
[OUT]
3-2-3.カーネル密度推定:az.plot_kde
点データから(密度)分布を推定する手法がカーネル密度関数(kernel density estimation)です。
PyMC3では"arviz.plot_kde()"で実装できます。
[IN]
az.plot_kde(x_sample)
[OUT]
4.関数・計算:Math
PyMC3の関数で数学で使用する関数計算が可能です。


4-1.三角関数
関数は"pm.math.<メソッド名>"で使用します。取得したデータはtheanoクラス型であるため"eval()"でNumpy型に変換すると扱いやすくなります。
[IN]
x = np.linspace(-2*np.pi, 2*np.pi, 100)
_samples = pm.math.sin(x)
print(_samples)
print(type(_samples))
samples = _samples.eval() #サンプリング結果を取り出す
print(type(samples))
plt.plot(x, samples)[OUT]
Elemwise{sin,no_inplace}.0
<class 'theano.tensor.var.TensorVariable'>
<class 'numpy.ndarray'>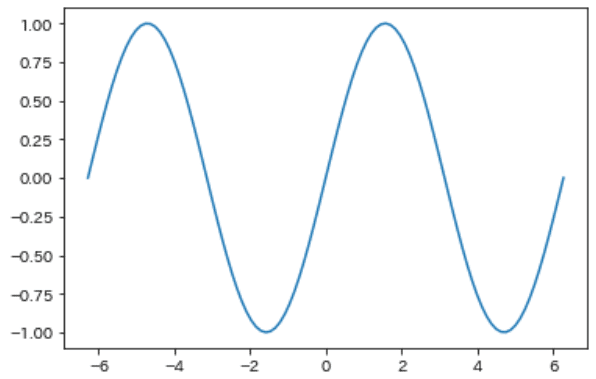
4-2.線形代数
線形代数ととして内積の計算は下記の通りです。
$$
\bf a = \begin{bmatrix}1 \\ 2 \\ 3\end{bmatrix},
b =\begin{bmatrix}4 \\ 5 \\ 6\end{bmatrix}
$$
$$
\bf a^T \cdot b= \begin{bmatrix}1 & 2 & 3\end{bmatrix}\cdot \begin{bmatrix}4 \\ 5 \\ 6\end{bmatrix}=4+10+18=32
$$
[IN]
a = np.array([1,2,3])
b = np.array([4,5,6])
pm.math.dot(a,b).eval()[OUT]
array(32)5.確率分布
PyMC3では様々な確率分布からサンプリング可能です。
5-1.一様分布
5-1-1.制約付きの一様分布:pymc.Uniform
一様分布は下記の通りであり、一様分布でサンプリングできる範囲(lower~upper)を指定します。
[API]
class pymc.Uniform(name, *args, rng=None, dims=None, initval=None,
observed=None, total_size=None, transform=UNSET, **kwargs)[IN]
with pm.Model() as model:
dist_uniform = pm.Uniform('theta', lower=0, upper=1) # 一様分布
trace = pm.sample(1000, chains=1)
data = trace.theta
print(data[:10])
print(az.summary(trace, var_names=['theta']).T)
sns.histplot(data, kde=True)
[OUT]
[0.82903692 0.31166821 0.23564582 0.56570981 0.41735873 0.66742444
0.22041811 0.06702037 0.94843952 0.94843952]
theta
mean 0.502
sd 0.293
hdi_3% 0.018
hdi_97% 0.950
mcse_mean 0.015
mcse_sd 0.010
ess_bulk 415.000
ess_tail 520.000
r_hat NaN
なお分布はwith構文でモデルの直下に記載せず。random()メソッドで直接サンプリングも可能です。
[IN]
dist_uniform = pm.Uniform.dist(lower=0, upper=1)
datas = dist_uniform.random(size=1000)
print(datas[:10])
print(az.summary(trace, var_names=['theta']).T)
sns.histplot(datas, kde=True)5-1-2.無制約の一様分布:pymc.Flat
pymc.Flatは定義域がすべての実数($${-\infin~\infin}$$)であり、この分布から直接サンプリングはできません。ベイズ分析の文脈では「無情報事前分布」(任意のパラメータ値に対して均等な確率を割り当てる)としてよく用いられます。
[API]
class pymc.Flat(*args, **kwargs)5-2.正規分布:pymc.Normal
正規分布は以下の通りです。
$$
f(x \mid \mu, \tau) = \sqrt{\frac{\tau}{2\pi}} \exp\left\{ -\frac{\tau}{2} (x-\mu)^2 \right\}
\\ (\tau = \dfrac{1}{\sigma^2})
$$
[API]
class pymc.Normal(name, *args, rng=None, dims=None, initval=None,
observed=None, total_size=None, transform=UNSET, **kwargs)[IN]
with pm.Model() as model:
dist = pm.Normal('theta', mu=0, sigma=1) # 正規分布
trace = pm.sample(1000, chains=1)
data = trace.theta
print(data[:10])
print(az.summary(trace, var_names=['theta']).T)
sns.histplot(data, kde=True)
[OUT]
[-0.49303715 -1.03823163 1.05351433 1.13783181 2.79981801 0.18175262
0.54652486 0.85026404 -0.86551757 0.89861053]
theta
mean 0.023
sd 1.021
hdi_3% -1.819
hdi_97% 2.092
mcse_mean 0.048
mcse_sd 0.034
ess_bulk 459.000
ess_tail 646.000
r_hat NaN
5-3.ベータ分布:pymc.Beta
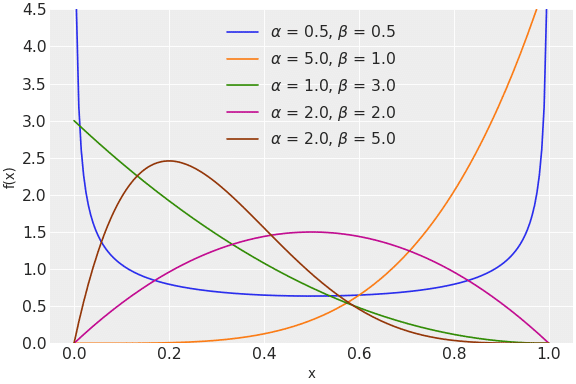
ベータ分布は以下の通りです。
$$
f(x \mid \alpha, \beta) = \frac{x^{\alpha - 1} (1 - x)^{\beta - 1}}{B(\alpha, \beta)}
$$
[API]
class pymc.Beta(name, *args, rng=None, dims=None, initval=None,
observed=None, total_size=None, transform=UNSET, **kwargs)[IN]
with pm.Model() as model:
dist = pm.Beta('theta', alpha=1, beta=4) # ベータ分布
trace = pm.sample(1000, chains=1)
data = trace.theta
print(data[:10])
print(az.summary(trace, var_names=['theta']).T)
sns.histplot(data, kde=True)
[OUT]
[0.12529662 0.12529662 0.11130926 0.11130926 0.12496253 0.12496253
0.04920355 0.03597303 0.03495444 0.0777443 ]
theta
mean 0.186
sd 0.158
hdi_3% 0.000
hdi_97% 0.502
mcse_mean 0.007
mcse_sd 0.005
ess_bulk 418.000
ess_tail 296.000
r_hat NaN
5-4.二項分布:pymc.Binomial
2項分布は以下の通りです。
$$
f(x \mid n, p) = \binom{n}{x} p^x (1-p)^{n-x}
$$
[API]
class pymc.Binomial(name, *args, **kwargs)[IN]
with pm.Model() as model:
dist = pm.Binomial('theta', n=10, p=0.5) # 二項分布
trace = pm.sample(1000, chains=1)
data = trace.theta
print(data[:10])
print(az.summary(trace, var_names=['theta']).T)
sns.histplot(data, kde=True)
[OUT]
[5 5 5 6 6 5 5 5 5 5]
theta
mean 4.783
sd 1.601
hdi_3% 2.000
hdi_97% 7.000
mcse_mean 0.101
mcse_sd 0.072
ess_bulk 251.000
ess_tail 268.000
r_hat NaN
5-5.ベルヌーイ分布:pymc.Bernoulli
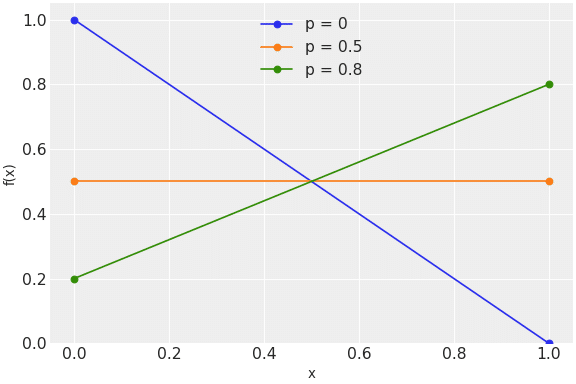
ベルヌーイ分布は以下の通りです。
$$
f(x \mid p) = p^{x} (1-p)^{1-x}
$$
[API]
class pymc.Bernoulli(name, *args, **kwargs)[IN]
with pm.Model() as model:
dist = pm.Bernoulli('theta', p=0.5) # ベルヌーイ分布
trace = pm.sample(1000, chains=1)
data = trace.theta
print(data[:10])
print(az.summary(trace, var_names=['theta']).T)
sns.histplot(data, kde=True)[OUT]
[0 0 1 0 1 1 1 0 0 1]
theta
mean 0.505
sd 0.500
hdi_3% 0.000
hdi_97% 1.000
mcse_mean 0.009
mcse_sd 0.006
ess_bulk 3000.000
ess_tail 1000.000
r_hat NaN
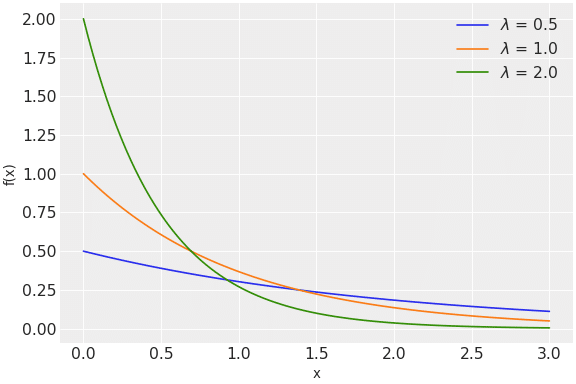
5-6.指数分布:pymc.Exponential
指数分布は以下の通りです。
$$
f(x \mid \lambda) = \lambda \exp\left\{ -\lambda x \right\}
$$
[API]
class pymc.Exponential(name, *args, rng=None, dims=None, initval=None, observed=None,
total_size=None, transform=UNSET, **kwargs)[IN]
import pymc3 as pm
import arviz as az
import seaborn as sns
x = np.linspace(0, 3, 100)
with pm.Model() as model:
dist1 = pm.Exponential('lambda_', 0.5)
trace1 = pm.sample(1000)
data1 = trace1.lambda_
print(data1[:5])
print(az.summary(data1))
sns.histplot(data1, kde=True, stat='density', color='blue')[OUT]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [lambda_]
100.00% [8000/8000 00:03<00:00 Sampling 4 chains, 11 divergences]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 20 seconds.
There were 10 divergences after tuning. Increase `target_accept` or reparameterize.
There was 1 divergence after tuning. Increase `target_accept` or reparameterize.
[3.40909766 3.12270747 2.18597695 1.94324143 0.47510031]
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
x 1.979 2.053 0.006 5.793 0.047 0.033 1347.0 1224.0 NaN 
6.事後分布
モデル内で事前分布とデータから得られる尤度から事後分布を作成することが可能です。事後分布の詳細は下記記事に記載しています。
サンプルとしてコイントス(ベルヌーイ試行)において、事前分布をベータ分布の一様分布、尤度をベルヌーイ分布として事後分布を作成しました。この時ベルヌーイ分布(尤度関数)にはベータ分布(事前分布)の変数を渡しています。
結果としてα=1, β=1のベータ分布は一様分布と同じ形になるのですが、尤度関数で渡したベルヌーイ分布により、事後分布が1の方へ寄っていることが確認できました。
[IN]
sampledata = np.array([0, 1, 1, 1, 1, 1, 1, 1, 1, 1])
with pm.Model() as model:
theta = pm.Beta('theta', alpha=1, beta=1) # ベータ分布(共役事前分布)
dist = pm.Bernoulli('x', p=theta, observed=sampledata) # ベルヌーイ分布
trace = pm.sample(1000, chains=1, return_inferencedata=True) # 事後分布のサンプリング[IN]
y = trace.posterior.theta.values
sns.histplot(y.ravel(), kde=True)
[OUT]
6-1.事後分布の可視化:az.plot_posterior
事後分布は"az.plot_posterior()"または"pm.plot_posterior()"で可視化できます。
[IN]
az.plot_posterior(trace, point_estimate='mode')
[OUT]
7.推論
sklearnのBostonデータセットを使用して簡単に計算してみました。
[IN]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib
import pymc3 as pm
from sklearn import datasets
boston = datasets.load_boston()
datas, target = boston.data, boston.target
_df = pd.DataFrame(np.concatenate([datas, target.reshape(-1, 1)], axis=1),
columns=boston.feature_names.tolist() + ['target'])
df = _df[['RM', 'target']].copy()
df_small = df.sample(10, random_state=0)
with pm.Model() as model:
# 事前分布
intercept = pm.Normal('intercept', mu=0, sd=10) # 切片
slope = pm.Normal('slope', mu=0, sd=10) # 係数
sigma = pm.HalfNormal('sigma', sd=1) # 予測の誤差
# モデル
mu = intercept + slope * df_small['RM']
# 尤度
likelihood = pm.Normal('likelihood', mu=mu, sd=sigma, observed=df_small['target'])
# 事後分布のサンプリング
trace = pm.sample(1000, chains=2, random_seed=0)
with model:
pm.plot_trace(trace)
pm.plot_posterior(trace)
[OUT]

[IN]
with model:
ppc = pm.sample_posterior_predictive(trace, random_seed=0)
# 予測値の平均を計算
preds = ppc['y'].mean(axis=0)
# 元のデータと予測値をプロット
plt.scatter(df['RM'], df['target'], label='Observed data')
plt.scatter(df_small['RM'], preds, color='red', label='Predicted data')
plt.xlabel('RM')
plt.ylabel('target')
plt.legend()
plt.show()
[OUT]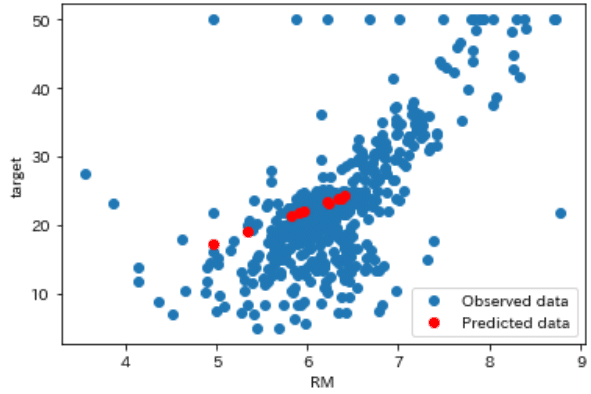
参考資料
あとがき
なんか使いにくいし分かりにくいと感じるのは自分だけ??
どちらにしろ高度な内容なので使いこなすのも一苦労だけど、そもそもライブラリの学習コストが高いのでいったん打ち切り
