
Pythonフレームワーク:Pytorch_学習モデル作成/全結合(Deep Learning)編
1.概要
前回の記事ではPytorchの基本的な操作/環境構築を紹介しました。本記事では学習モデル作成やモデルの操作方法などを学びます。
2.事前の学習ポイント・注意点
2-1.ライブラリ
もしエラーになったら、エラー文に合わせて必要なライブラリをインポートします。
[Terminal]
pip install torchviz
pip install torchinfo2-2.Pytorchで学習モデル(全結合)作成時の注意点
Pytorchで全結合モデル(NN)を作成時の注意点・ポイントを紹介します。
【Pytorchの実装】
NNでは入力値が「0~1」または「-1~1」で高性能となる。よって入力値は標準化や正規化などの前処理をした方がよい
入力値の型式はfloat32にすること。Numpy型からテンソルを作成するとfloat64になるためそのままだとエラーになる。
モデルの重みwは拡張しやすいように行列形状[r, c]であり1つのwでも[1,1]となる。行列計算ができるように入力値の形状を重みに合わせる必要がある(1つのwの場合入力値の形状は(N, 1)が正。(N, )だとエラー)。
ラベルデータ(正解値)の形状も行列形状のため(N, 1)にする必要がある。また分類問題の時は整数(int)が必要な時があるため注意(tensor.long()で変換)
勾配情報を持つパラメータは直接更新できないため"torch.no_grad()"か"最適化関数"を使用する
パラメータ更新後に勾配情報は自動的に0にならないため”初期化(0にする)”処理が必要
メソッドの後ろに"_"があるものは"変数の上書き"を意味している。
【モデル作成】
学習時は「学習(train), 検証(val), テスト(test)」用のデータに分割すべき
決定木と異なり全結合ではNoneは受け付けないため欠損値処理は必要
後で再現性がとれるように乱数値もロギングしておいた方がよい。
深層学習(全結合)=「特徴量をすべてモデルが抽出して最強」のイメージがあったが比較的ハイパーパラメータが多く(学習率η、ノード数、レイヤ数、過学習防止(dropout, norm)など)、かつ特徴量エンジニアリング(入力するデータの整理)の影響も大きいため万能ではない。
3.Pytorchの基本操作
今回のNN実装において基礎操作(前回記事と重複あり)紹介します。
3-1.テンソル作成:torch.tensor
全結合も考慮した時のtensorの引数は下記の通りです。
【torch.tensor()の引数】
●dtype:データの型式設定(入力値はfloat32をよく使用する)
●names:テンソルに名前を設定
●requires_grad:backward()で逆伝搬による勾配データを取得できる
●device:どのデバイス(CPU/GPU)にテンソルを載せるか設定
テンソルの作成は①pytorchで直接、②Numpy型から作成することが出来ます。backward()が実行できるようにするためには(a)テンソル変数作成時に指定、(b)属性から設定することが可能です。
Numpy型からテンソル作成するとdtype=float64になりエラーの原因となるためdtype指定が必要です。また"torch.from_numpy(<ndarray>)"からも作成可能ですがdtypeはnumpyの方で指定しておく必要があります。
[IN]
import torch
import numpy as np
#Numpyから作る場合
t_numpy1 = torch.tensor(np.arange(-2, 2.1, 1.0))
t_numpy2 = torch.tensor(np.arange(-2, 2.1, 1.0),
dtype = torch.float32, #設定しないとtorch.float64になる
requires_grad=True)
#Tensorから作る場合
t_torch = torch.arange(-2, 2.1, 1.0)
t_torch.requires_grad = True
print('numpyから変換(指定なし):', t_numpy1.dtype, '\n',
'numpyから変換(dtype指定):', t_numpy2.dtype, '\n',
'torchで作成:', t_torch.dtype)
print(t_numpy2, t_torch)
[OUT]
numpyから変換(指定なし): torch.float64
numpyから変換(dtype指定): torch.float32
torchで作成: torch.float32
tensor([-2., -1., 0., 1., 2.], requires_grad=True)
tensor([-2., -1., 0., 1., 2.], requires_grad=True)【参考:変数名の設定】
変数への名前設置(names引数)は自分で作成するテンソルには使用しませんがnn.Moduleの継承時や事前学習モデル使用時にはデータが設定されているため理解は必要です。
[IN]
t_1dim = torch.tensor([1.0, 2.0, 3.0], names=['KIYO'])
print(t_1dim, t_1dim.shape)
t_2dim = torch.tensor([[1.0, 2.0, 3.0]], names=['KIYO1', 'KIYO2'])
print(t_2dim, t_2dim.shape)
print(t_2dim[0].names)
[OUT]
tensor([1., 2., 3.], names=('KIYO',)) torch.Size([3])
tensor([[1., 2., 3.]], names=('KIYO1', 'KIYO2')) torch.Size([1, 3])
('KIYO2',)3-2.テンソルの情報抽出(勾配・GPU)
テンソルが保有するデータ確認方法(属性)は下記の通りです。
【テンソルの情報】
●grad:backward()後に計算される勾配データ
●names:テンソルに設定された名前
●device:テンソルがどのデバイス(CPU/GPU)にいるか出力
●is_cuda:cuda(GPU)上にあるかどうかをTrue/Falseで出力
【前回記事記載】
●shape:テンソルの形状
●size():テンソルの形状->shapeとほぼ同じ(※numpyのsizeとは異なる)
●dtype:テンソル内のデータ型
●ndim:テンソルの次元数
●numel():テンソル全体のパラメータ数 (※numpyのarray.sizeと同じ)
4.GPU(CUDA)の使用
4-1.CUDA環境の確認
CUDA設定済みの環境であればGPUを使用して計算が可能です。仕様は下記コードで確認できます。
[IN]
import torch
print('version:', torch.__version__) #PytorchのVersion
print('GPU名:', torch.cuda.get_device_name(0)) #PCのGPU名を表示
print('GPU数:', torch.cuda.device_count()) #GPUの数を表示
print('CUDAのindex:', torch.cuda.current_device()) #CUDAのindexを表示
print('GPU使用:',torch.cuda.is_available()) #GPUが使えるかどうか
[OUT]
version: 1.8.0+cu111
GPU名: NVIDIA GeForce RTX 2060 SUPER
GPU数: 1
CUDAのindex: 0
GPU使用: True4-2.デバイス設定/CUDAへの割り当て
PytorchでGPUを使用する時には下記ルールがあります。
テンソル変数にデバイス(CPU/GPU)を割り当てる(defalut:cpu)
基本的にはモデル(net)もデバイス(CPU/GPU)を割り当てが必要
変数同士を演算する場合は同じデバイスを割り当てる必要がある※スカラー値の場合はGPU側に自動的に割り当てられる
デバイスが異なる場合は"toメソッド"でデバイスを割り当てる
デバイス作成は"torch.device(<cpu/gpu>)"となります。If文を使用するとGPU使用可能な場合は自動で割り当てます。
[IN]
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu') #GPUが使える場合はDeviceをGPUに設定
print(device)
[OUT]
cuda:0deviceの割り当てはテンソル作成時や”tensor.to(device)"で指定可能です。参考までに一般/省略形の記法を下記に記載します。なおモデルも"Net().to(device)"で移動可能です。
【テンソルをデバイスに割り当て:CPU->GPU】
●tensor.to(device):deviceオブジェクトに割り当てたデバイスを設定
●tensor.to('cuda:0'):1個目のGPUに配置(GPU数はdevice_count()で確認)
●tensor.cuda(0):tensor.to('cuda:0')と同じ
●tensor.cuda():自動で最初のGPUに配置
【テンソルをデバイスに割り当て:GPU->CPU】
●tensor.to('cpu'):cpuに配置
●tensor.cpu():tensor.to('cpu')と同じ
[IN]
tensor1 = torch.tensor([2])
tensor2 = torch.tensor([3], device=torch.device('cuda:0')) #GPUにTensorを作成
print(tensor1, tensor2)
print('t1のdevice:', tensor1.device, 't2のdevice:', tensor2.device) #Device上のテンソル(変数)の位置(CPU or GPU)を表示
print(tensor1.is_cuda, tensor2.is_cuda) #テンソル(変数)がGPU上にあるかどうか確認
tensor1 = tensor1.to(device) #テンソル(変数)をGPUに移動
print(tensor1)
print(tensor1+tensor2)
[OUT]
tensor([2]) tensor([3], device='cuda:0')
t1のdevice: cpu t2のdevice: cuda:0
False True
tensor([2], device='cuda:0')
tensor([5], device='cuda:0')【CPUとGPUでの計算によるエラー発生の確認】
ルールの通りスカラー値であればCPU/GPUの計算でもエラーは出ませんが、テンソルだとエラーが発生します。
[IN]
_t1, _t2 = torch.tensor(1), torch.tensor(2, device=torch.device('cuda:0'))
print(_t1+_t2)
t1, t2 = torch.tensor([3]), torch.tensor([4], device=torch.device('cuda:0'))
print(t1+t2)
[OUT]
tensor(3, device='cuda:0')
RuntimeError: Expected all tensors to be on the same device, but found at least two devices, cuda:0 and cpu!4-3.CUDAでの乱数値固定:torch.backends.cudnn.benchmark
乱数シードを固定する場合はmanua._seed()を使用します(上コード参照)。しかしCUDA(GPU)を使用する場合は上だけでは完全に値を再現できないため下コードを実行します。
注意点として下コード(GPUの固定)を設定するとGPUの計算速度が遅くなる場合があるとのことです。
[IN]
seed = 0
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)torch.backends.cudnn.benchmark = False
torch.use_deterministic_algorithms = True4-4.エラー対応1:CUDA out of memory
GPUのメモリに乗らないほどのデータを転送すると生じるエラーです。対処法として下記があります。
前の処理で残っているメモリを開放する(つまり再起動)
入力するデータのサイズ(ミニバッチ)を小さくする->学習用(train)だけじゃなく、検証用(val)を推論する時のデータ数も小さくすること
5.深層学習用モジュール:torch.nn
Pytorchにはニューラルネットワーク(深層学習)を簡単にするためのモジュールとして"torch.nn"があり、パラメータ(変数)の有無で使い分けます。
【torch.nn】
●torch.nn:パラメータ有り(Linearモデル, 畳み込み(Conv2d)など)
●torch.nn.functional as F:パラメータ無し
->ReLU, sigmoid, dropoutなど
->F.method()はインスタンス化できないため直接使用しないならnnを使用
全結合や活性化関数などはレイヤ(層)と表現されており、torch.nnを利用することで各種レイヤを追加できます。
5-1.Affineレイヤ(全結合):nn.Linear()
全結合層(Affineレイヤ)はnn.Linear()で作成します。サンプルとして3種類のモデルを作成しました。

[IN]
import torch
import torch.nn as nn
import torch.nn.functional as F
torch.manual_seed(0) #乱数のシードを設定
model = nn.Linear(1, 1) #入力1、出力1の線形層(wx+b)を作成
model2 = nn.Linear(3, 1) #入力1、出力1の線形層(wx+b)を作成
model3 = nn.Linear(2, 2) #入力1、出力1の線形層(wx+b)を作成
print(model)
print(model.weight); print(model.bias)
print(model2)
print(model2.weight); print(model2.bias)
print(model3)
print(model3.weight); print(model3.bias)
[OUT]
Linear(in_features=1, out_features=1, bias=True)
Parameter containing:
tensor([[-0.0075]], requires_grad=True)
Parameter containing:
tensor([0.5364], requires_grad=True)
Linear(in_features=3, out_features=1, bias=True)
Parameter containing:
tensor([[-0.4752, -0.4249, -0.2224]], requires_grad=True)
Parameter containing:
tensor([0.1548], requires_grad=True)
Linear(in_features=2, out_features=2, bias=True)
Parameter containing:
tensor([[-0.0140, 0.5607],
[-0.0628, 0.1871]], requires_grad=True)
Parameter containing:
tensor([-0.2137, -0.1390], requires_grad=True)モデルを使用して計算する場合はオブジェクトにそのまま数値を渡せば計算できます。ただし重みwの形状が(1, N)となっているため、行列計算できるように入力値を(N,1)形状に変換する必要があります。
[IN]
torch.manual_seed(0) #乱数のシードを設定
model = nn.Linear(1, 1) #入力1、出力1の線形層(wx+b)を作成
_x = torch.tensor([1.0, 2.0]) #そのままだとRuntimeError: mat1 and mat2 shapes cannot be multiplied (1x2 and 1x1)
x = _x.reshape(-1, 1) #1次元配列を2次元配列に変換
y_pred = model(x)
print(x, y_pred)
print(_x.shape, _x.dtype)
print(x.shape, x.dtype)
print(y_pred.shape, y_pred.dtype)
[OUT]
tensor([[1.],
[2.]])
tensor([[0.5290],
[0.5215]], grad_fn=<AddmmBackward>)
torch.Size([2]) torch.float32
torch.Size([2, 1]) torch.float32
torch.Size([2, 1]) torch.float325-2.モデルパラメータの確認:parameters/state_dict
モデルのパラメータ確認方法は下記の通りです。
【パラメータ確認方法】
●model.state_dict():{'weight名': <wの値>, 'bias名':<bの値>}の順序付き辞書の形で出力
●model.named_parameters():変数名と値を確認
●model.parameters():値のみ確認
※出力は両方ともジェネレーターのためfor文で抽出する
【state_dict()】
[IN]
print(model.state_dict())
[OUT]
OrderedDict([('weight', tensor([[-0.0075]])), ('bias', tensor([0.5364]))])【named_parameters()】
[IN]
_ = next(iter(model.named_parameters()))
print(model.named_parameters(), 'データ数:', len(_), 'データ型', type(_))
for param in model.named_parameters():
print('name:', param[0])
print('value:', param[1], 'データ形状:', param[1].shape) #勾配はTrue
[OUT]
<generator object Module.named_parameters at 0x000001FF6EB45B30> データ数: 2 データ型 <class 'tuple'>
name: weight
value: Parameter containing:
tensor([[-0.0075]], requires_grad=True) データ形状: torch.Size([1, 1])
name: bias
value: Parameter containing:
tensor([0.5364], requires_grad=True) データ形状: torch.Size([1])【parameters()】
[IN]
_ = next(iter(model.parameters()))
print(model.parameters(), 'データ数:', len(_), 'データ型', type(_))
for param in model.parameters():
print('value:', param[0], 'データ形状:', param[0].shape)
[OUT]
<generator object Module.parameters at 0x000001FF6EB45B30> データ数: 1 データ型 <class 'torch.nn.parameter.Parameter'>
value: tensor([-0.0075], grad_fn=<SelectBackward>) データ形状: torch.Size([1])
value: tensor(0.5364, grad_fn=<SelectBackward>) データ形状: torch.Size([]) なお後述するカスタムクラス(nn.Module)で作成したクラスでは"dict
(net.named_parameters())"を実行すると"{'param名':param値(tensor)}"を取得できます。
[IN]
dict(net.named_parameters())
[OUT]
{'f1.weight': Parameter containing:
tensor([[1.5410]], device='cuda:0', requires_grad=True),
'f1.bias': Parameter containing:
tensor([1.], device='cuda:0', requires_grad=True)}5-3.パラメータの設定(初期化):nn.init
通常はランダム値でパラメータが初期化されますが手動で値を設定したい場合はnn.init.constant_(<parameter>,<値>)を使用します。またdata.fill_でも代用可能です。※"_"付きメソッドのため変数は自動で上書きされます
[IN]
nn.init.constant_(model.weight, 1.5410)
nn.init.constant_(model.bias, 1.0)
print(model.weight, model.bias)
[OUT]
Parameter containing:
tensor([[1.5410]], requires_grad=True)
Parameter containing:
tensor([1.], requires_grad=True)[IN]
model.weight.data.fill_(1.5410), model.bias.data.fill_(1.0)
print(model.weight, model.bias)
[OUT]
Parameter containing:
tensor([[1.5410]], requires_grad=True)
Parameter containing:
tensor([1.], requires_grad=True)またHeの初期値など重みの最適初期値の選定なども可能です。
5-4.活性化関数レイヤ
5-4-1.活性関数一覧
一般的な活性化関数は下記の通りです。
【活性関数一覧】
●ReLU関数:x<0ではy=0, x>0ではy=xの関数であり勾配消失に強い
●LeakyReLU関数:ReLUとほぼ同じだがx<0で傾きのあるy=axを使用
●TANH関数:ー
●Sigmoid関数:
ー>昔は使用されたがDeepなモデルで勾配消失が発生する問題がある
ー>0~1内のデータとなるため2値分類での確率として出力可能
ー>値が過剰な箇所(e.g. ±1e^100)では勾配が小さいため学習しにくい
何個か検証しましたがTAHNやSigmoid関数はnn.functionalでは非推奨のためtorchで作成します。説明用コードとして可視化したグラフも紹介します。
[IN]
import torch
import torch.nn as nn
import torch.nn.functional as F
import matplotlib.pyplot as plt
import japanize_matplotlib
t = torch.tensor([-3.0, -2.0, -1.0, 0.0, 1.0, 2.0, 3.0])
print('ReLu:', F.relu(t)) # ReLU関数
print('TANH:', torch.tanh(t)) # TAHN関数(F.tanhは非推奨)
print('Sigmoid:', torch.sigmoid(t)) # Sigmoid関数(F.sigmoidは非推奨)
print('Leaky ReLu:', F.leaky_relu(t)) # Leaky ReLU関数
print('Softplus:', F.softplus(t)) # Softplus関数
[OUT]
ReLu: tensor([0., 0., 0., 0., 1., 2., 3.])
TANH: tensor([-0.9951, -0.9640, -0.7616, 0.0000, 0.7616, 0.9640, 0.9951])
Sigmoid: tensor([0.0474, 0.1192, 0.2689, 0.5000, 0.7311, 0.8808, 0.9526])
Leaky ReLu: tensor([-0.0300, -0.0200, -0.0100, 0.0000, 1.0000, 2.0000, 3.0000])
Softplus: tensor([0.0486, 0.1269, 0.3133, 0.6931, 1.3133, 2.1269, 3.0486])[IN]
x = torch.arange(-3.0, 3.0, 0.1)
fig = plt.figure(figsize=(15, 10))
ax1, ax2, ax3, ax4, ax5 = fig.add_subplot(2, 3, 1), fig.add_subplot(2, 3, 2), fig.add_subplot(2, 3, 3), fig.add_subplot(2, 3, 4), fig.add_subplot(2, 3, 5)
ax1.plot(x, F.relu(x), label='ReLU'), ax2.plot(x, torch.tanh(x), label='TANH'), ax3.plot(x, torch.sigmoid(x), label='Sigmoid'), ax4.plot(x, F.leaky_relu(x, 0.1), label='Leaky ReLU'), ax5.plot(x, F.softplus(x), label='Softplus')
ax1.set_ylim(-3, 3), ax2.set_ylim(-3, 3), ax3.set_ylim(-3, 3), ax4.set_ylim(-3, 3), ax5.set_ylim(-3, 3), ax1.legend(), ax2.legend(), ax3.legend(), ax4.legend(), ax5.legend(), ax1.grid(), ax2.grid(), ax3.grid(), ax4.grid(), ax5.grid(), plt.show()
plt.figure()
[OUT]
なお活性化関数ではないですがSoftmax関数も使用可能です。
[IN]
out = F.softmax(t, dim=0)
print('Softmax:', out, out.sum()) # Softmax関数
[OUT]
Softmax: tensor([0.0114, 0.0281, 0.0843, 0.2533, 0.6229]) tensor(1.)5-4-2.メモリの節約:inplace=True
活性化関数には引数"inplace"があります。動作から確認できるように"inplace=True"を設定すると入力に使用したデータが上書きされます。
これにより関数への入力値が保持されないためメモリ節約ができます。
[IN]
import torch
import torch.nn.functional as F
#Tensor作成※t1, t2は同じ
t1, t2 = torch.tensor([-2.0, -1.1, 0.0, 1.1, 2.0]), torch.tensor([-2.0, -1.1, 0.0, 1.1, 2.0])
t1_relu = F.relu(t1) # ReLU関数
print(f't1(Inplace無し): {t1}') #Inplace無し
print(f'Relu:{t1_relu}', end='\n\n') #Inplace無し
t2_relu = F.relu(t2, inplace=True) # ReLU関数
print(f't2(Inplace有り): {t2}') #Inplace有り
print(f'Relu:{t2_relu}') #Inplace有り
[OUT]
t1(Inplace無し): tensor([-2.0000, -1.1000, 0.0000, 1.1000, 2.0000])
Relu:tensor([0.0000, 0.0000, 0.0000, 1.1000, 2.0000])
t2(Inplace有り): tensor([0.0000, 0.0000, 0.0000, 1.1000, 2.0000])
Relu:tensor([0.0000, 0.0000, 0.0000, 1.1000, 2.0000])5-5.過学習防止(レイヤ)
過学習防止対策は下記の通りである。
【過学習防止手法】
●Dropout:全結合の一部を結合させずに使うことで過学習防止
->パラメータはないためF.Dropout()で使用可能
->ノードの接続割合pは設定が必要
->入力値との全体平均を合わせるため出力値は1/(1-p)倍となる
->過学習防止の反面、学習時間が長くなるデメリットがある
●BatchNormalization:バッチ正規化
->nn.BatchNorm1dとnn.BatchNorm2dがある。2dは画像で使用
->BatchNormはパラメータを持つためnnモジュールから使用
->活性化関数の前のレイヤに配置することが多い
->BN関数は自信のパラメータがあり学習の対象である。よってモデル作成時は必ず1つのBNレイヤにつき1個定義する必要がある(一つのレイヤを複数個所に使用できない)。
5-5-1.Dropout
[IN]
torch.manual_seed(12)
t = torch.tensor([1,2,3,4,5,6,7,8,9,10]).float()
dropout = nn.Dropout(p=0.3) # pはドロップアウトする確率
#訓練モードで検証
dropout.train() # 訓練モード
print('学習モード:', dropout.training)
print(dropout(t)) #出力が1/(1-p)倍される->入力値全体の平均を揃える
#検証モード
dropout.eval() # 検証モード
print('学習モード:', dropout.training)
print(dropout(t))
[OUT]
学習モード: True
tensor([ 0.0000, 2.8571, 4.2857, 5.7143, 0.0000, 8.5714, 10.0000, 11.4286,
0.0000, 14.2857])
学習モード: False
tensor([ 1., 2., 3., 4., 5., 6., 7., 8., 9., 10.])5-5-2.Batch Normalization
[IN]
t = torch.tensor([[1,2,3],[4,5,6]]).float()
norm1d = nn.BatchNorm1d(3)
norm1d(t)
[OUT]
tensor([[-1.0000, -1.0000, -1.0000],
[ 1.0000, 1.0000, 1.0000]], grad_fn=<NativeBatchNormBackward>)5-6.レイヤー結合モデルの作成1:nn.Sequential
全結合は各レイヤを重ね合わせて作る合成関数です。例として2つの線形関数から合成関数を作る場合のコードは下記の通りです。
$$
f_{1}(x)=3x\\
f_{2}(x)=2x+1\\
f_{g}(x)=f_{2}(f_{1}(x))=6x+1\\
$$
[IN]
import torch
import torch.nn as nn
from torchinfo import summary
m1, m2 = nn.Linear(1, 1), nn.Linear(1, 1) #入力1、出力1の線形層(y=wx+b)
#m1: y=3x
nn.init.constant_(m1.weight, 3.0)
nn.init.constant_(m1.bias, 0.0)
#m2: y=2x+1
nn.init.constant_(m2.weight, 2.0)
nn.init.constant_(m2.bias, 1.0)
#入力値
x = torch.tensor([1.0, 2.0, 3.0]).unsqueeze(1) #unsqueeze(1)で次元を追加->torch.Size([3, 1])
#合成関数の作成
out1 = m1(x) #m1の出力
out2 = m2(out1) #m2の出力
print(out2)
[OUT]
tensor([[ 7.],
[13.],
[19.]], grad_fn=<AddmmBackward>) "nn.Sequential"を使用することで合成関数をパイプラインのように一つのオブジェクトにまとめることができます。また後述するsummary表示により各レイヤの情報を一元管理することが出来ます。
これをうまく使用すれば全結合の中間層の数を効率的に作成可能です。
[IN]
sequential = nn.Sequential(
m1,
m2
)
print(sequential, end='\n\n')
for idx, (name, param) in enumerate(sequential.named_parameters()):
print(idx)
print(name)
print(param)
out = sequential(x)
print(out)
print(summary(sequential, input_size=(1, 1)))
[OUT]
Sequential(
(0): Linear(in_features=1, out_features=1, bias=True)
(1): Linear(in_features=1, out_features=1, bias=True)
)
0
0.weight
Parameter containing:
tensor([[3.]], requires_grad=True)
1
0.bias
Parameter containing:
tensor([0.], requires_grad=True)
2
1.weight
Parameter containing:
tensor([[2.]], requires_grad=True)
3
1.bias
Parameter containing:
tensor([1.], requires_grad=True)
tensor([[ 7.],
[13.],
[19.]], grad_fn=<AddmmBackward>)
==========================================================================================
Layer (type:depth-idx) Output Shape Param #
==========================================================================================
Sequential -- --
├─Linear: 1-1 [1, 1] 2
├─Linear: 1-2 [1, 1] 2
==========================================================================================
Total params: 4
Trainable params: 4
Non-trainable params: 0
Total mult-adds (M): 0.00
==========================================================================================
Input size (MB): 0.00
Forward/backward pass size (MB): 0.00
Params size (MB): 0.00
Estimated Total Size (MB): 0.00
==========================================================================================なおnn.SequentialはOrderedDictを渡せるため、各レイヤに名前を付けることもできます(※summaryの出力結果には変化なし)。
[IN]
from collections import OrderedDict
sequential2 = nn.Sequential(OrderedDict([
('Input Layer', m1),
('Output Layer', m2)
]))
print(sequential)
print(sequential2)
[OUT]
Sequential(
(0): Linear(in_features=1, out_features=1, bias=True)
(1): Linear(in_features=1, out_features=1, bias=True)
)
Sequential(
(Input Layer): Linear(in_features=1, out_features=1, bias=True)
(Output Layer): Linear(in_features=1, out_features=1, bias=True)
)5-7.レイヤー結合モデルの作成2:nn.ModuleList
"nn.Sequential"と似ておりますが、"nn.ModuleList"はListからレイヤを重ねていくことが出来ます。
前節のサンプルと同様に下記式を"nn.Modulelist"で作成しました。データの取得はFor文で処理します。
$$
f_{1}(x)=3x\\
f_{2}(x)=2x+1\\
f_{g}(x)=f_{2}(f_{1}(x))=6x+1\\
$$
[IN]
x = torch.tensor([1.0, 2.0, 3.0]).unsqueeze(1) #unsqueeze(1)で次元を追加->torch.Size([3, 1])
layers = [m1, m2]
modulelist = nn.ModuleList(layers)
print(modulelist, end='\n\n')
for idx, layer in enumerate(modulelist):
print(layer)
x_in = x
x = layer(x)
print(f'x->x:{x_in} -> {x}', end='\n\n')
print('Final x:', x)
[OUT]
ModuleList(
(0): Linear(in_features=1, out_features=1, bias=True)
(1): Linear(in_features=1, out_features=1, bias=True)
)
Linear(in_features=1, out_features=1, bias=True)
x->x:tensor([[1.],
[2.],
[3.]]) -> tensor([[3.],
[6.],
[9.]], grad_fn=<AddmmBackward>)
Linear(in_features=1, out_features=1, bias=True)
x->x:tensor([[3.],
[6.],
[9.]], grad_fn=<AddmmBackward>) -> tensor([[ 7.],
[13.],
[19.]], grad_fn=<AddmmBackward>)
Final x: tensor([[ 7.],
[13.],
[19.]], grad_fn=<AddmmBackward>)6.カスタムクラスの作成:nn.Module
より効率的にモデルを作成するためにPytorchにある親クラスnn.Moduleを使用してモデルを作成します。
6-1.nn.Moduleによるモデル作成要領
モデル作成時のポイントは下記の通りです。
nn.Moduleを継承して使い、"super().__init__()"で初期化する
順伝搬(推論用関数)は"forward()"で定義する。これにより"__call__"で定義しているように、メソッド名を使用せずにojbect(x)で推論(関数を実行)することが出来る。
下記に最もシンプルな記法で記載した。レイヤを重ねていくことで複雑な全結合モデルを作成することが可能になります。
[IN]
import torch
import torch.nn as nn #パラメータをもつレイヤ関数
import torch.nn.functional as F #パラメータをもたないレイヤ関数
class Net(nn.Module):
def __init__(self, n_in, n_out):
super().__init__() #nn.Moduleの継承(初期化呼び出し)
#レイヤの定義
self.f1 = nn.Linear(n_in, n_out) #入力層:n_in, 出力層:n_outの線形レイヤ
#重みの初期化
nn.init.constant_(self.f1.weight, 1.5410)
nn.init.constant_(self.f1.bias, 1.0)
def forward(self, x):
out = self.f1(x)
return out
torch.manual_seed(0) #乱数のシードを設定
net = Net(1, 1) #入力1、出力1の線形層(wx+b)を作成
out = net(torch.Tensor([1.0]).unsqueeze(1))
print('y=', out)
for param in net.named_parameters():
print('name:', param[0])
print('value:', param[1], 'データ形状:', param[1].shape) #勾配はTrue
for param in net.named_parameters():
print(param)
from torchinfo import summary
print(summary(net, input_size=(1, )))[OUT]
y= tensor([[2.5410]], grad_fn=<AddmmBackward>)
name: f1.weight
value: Parameter containing:
tensor([[1.5410]], requires_grad=True) データ形状: torch.Size([1, 1])
name: f1.bias
value: Parameter containing:
tensor([1.], requires_grad=True) データ形状: torch.Size([1])
('f1.weight', Parameter containing:
tensor([[1.5410]], requires_grad=True))
('f1.bias', Parameter containing:
tensor([1.], requires_grad=True))
==========================================================================================
Layer (type:depth-idx) Output Shape Param #
==========================================================================================
Net -- --
├─Linear: 1-1 [1] 2
==========================================================================================
Total params: 2
Trainable params: 2
Non-trainable params: 0
Total mult-adds (M): 0.00
==========================================================================================
Input size (MB): 0.00
Forward/backward pass size (MB): 0.00
Params size (MB): 0.00
Estimated Total Size (MB): 0.00
==========================================================================================6-2.net()の属性情報取得:net.layer名
nn.Moduleでモデルを作成すると自動でレイヤに名前が設定されます。名前はself.の後ろの文字となります。"net.<layer名>"とすると一つのモデルのように扱えるため下記メソッドが使用できます。
【使用できるメソッド】
●weight:モデル内の重みw
->requires_gradで勾配の調整が可能:転移学習やファインチューニング用
●bias:モデル内のバイアスb
●in_features:入力値のノード数(次元数)
●out_features:出力値のノード数(次元数)
●state_dict():変数名と値を辞書のOrderdictの形で取得
●named_parameters:変数名と値を確認
●parameters():値のみ確認
[IN]
class Net(nn.Module):
def __init__(self, n_in, n_out):
super().__init__() #nn.Moduleの継承(初期化呼び出し)
self.f1 = nn.Linear(n_in, 10)
self.relu = nn.ReLU(inplace=True)
self.f2 = nn.Linear(10, n_out)
def forward(self, x):
out = self.f1(x)
out = self.relu(x)
out = self.f2(x)
return out
net = Net(2, 1)
print(net, end='\n\n')
print(net.f1)
print(net.relu)
print(net.f2, end='\n\n')
#f1レイヤの情報抽出
print('w形状:', net.f1.weight.shape, 'bias形状:', net.f1.bias.shape)
print('入力ノード数:', net.f1.in_features, '出力ノード数', net.f1.out_features)
for name, param in net.f1.named_parameters():
print(name, param.shape, param.requires_grad)
print(net.f1.parameters())[OUT]
Net(
(f1): Linear(in_features=2, out_features=10, bias=True)
(relu): ReLU(inplace=True)
(f2): Linear(in_features=10, out_features=1, bias=True)
)
Linear(in_features=2, out_features=10, bias=True)
ReLU(inplace=True)
Linear(in_features=10, out_features=1, bias=True)
w形状: torch.Size([10, 2]) bias形状: torch.Size([10])
入力ノード数: 2 出力ノード数 10
weight torch.Size([10, 2]) True
bias torch.Size([10]) True
<generator object Module.parameters at 0x0000022DB2C5C740>【参考:モデル内の関数(属性)名の自動付与に関して】
モデル内に関数名がつくのは__init__()下で定義した場合のみであり、forward()内で使用した関数は定義されないことはご注意ください。

6-3.訓練/検証Phase:net.train()/eval()
作成したnetクラスにはnet.train()とnet.eval()があり、前者は学習時、後者は検証・テスト時に使用します。これはDropoutなど学習時とそれ以外で動作が異なるレイヤがあるためです。
6-4.応用編:パラメータの追加:nn.Parameter
nn.Moduleで作成したクラスをインスタンス化後は"state_dict()"や
"named_parameters()"でパラメータ(weightとbias)を確認できます。しかしそのパラメータは"nn.Linear()"や"nn.Conv2d"などで作成した物だけです。
下記の通りnn.Linearで作成したインスタンスはパラメータとして認識していますが、計算のために使用(追加)したnn.tensor()は認識されません。
[IN]
import torch
import torch.nn as nn #パラメータをもつレイヤ関数
class Net(nn.Module):
def __init__(self, n_input):
super().__init__() #nn.Moduleの継承(初期化呼び出し)
self.linear = nn.Linear(n_input, 1) #入力層:n_in, 出力層:n_outの線形レイヤ
self.add = torch.tensor(1.0, requires_grad=True) #追加する値※パラメータにはならない
def forward(self, x):
out = self.linear(x) + self.add
return out
#線形モデル(1次元)
linear = Net(1)
for name in linear.state_dict():
print(f'{name}: {linear.state_dict()[name]}')
[OUT]
linear.weight: tensor([[-0.7923]])
linear.bias: tensor([-0.5679]) 自動作成されないパラメータをモデルに追加したい場合は"nn.Parameter"
を使用します。
[torch.nn.parameter.Parameter]
torch.nn.parameter.Parameter(data=None,
requires_grad=True)"nn.Parameter"で追加した値はモデル内でパラメータとして認識されるようになりました。実際は”nn.Parameter(torch.rand(C, H, W))”のように乱数値などで使用します。
[IN]
import torch
import torch.nn as nn #パラメータをもつレイヤ関数
class Net(nn.Module):
def __init__(self, n_input):
super().__init__() #nn.Moduleの継承(初期化呼び出し)
self.linear = nn.Linear(n_input, 1) #入力層:n_in, 出力層:n_outの線形レイヤ
self.add = nn.Parameter(torch.tensor(1.0)) #バイアスを設定:固定値Ver.
def forward(self, x):
out = self.linear(x) + self.add
return out
#線形モデル(1次元)
linear = Net(1)
for name in linear.state_dict():
print(f'{name}: {linear.state_dict()[name]}')
[OUT]
add: 1.0
linear.weight: tensor([[0.8385]])
linear.bias: tensor([0.3511])7.モデルの再利用
7-1.モデルの保存:torch.save()
学習したモデルはPickleファイルとして"torch.save()"で保存可能です。
モデルの保存方法は下記2種があります。私がCNNモデル作成した時①は駄目で②は成功したことがあるため両方理解しておくと便利です。
モデルを保存:torch.save(<model obj>, <pickleファイル名>)
Paramを保存:torch.save(<model.state_dict()>, <pickleファイル名>)
【モデルを保存:torch.save(<model obj>, <pickleファイル名>)】
[IN]
import torch
import torch.nn as nn
import torch.nn.functional as F
#モデル
class Net(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(1, 1)
nn.init.constant_(self.linear.weight, 1), nn.init.constant_(self.linear.bias, 0)
def forward(self, x):
return self.linear(x)
net = Net()
torch.save(net, 'savemovel/test_model.pkl') #モデルの保存
[OUT]
【Paramを保存:torch.save(<model.state_dict()>, <pickleファイル名>)】
[IN]
import torch
import torch.nn as nn
import torch.nn.functional as F
#モデル
class Net(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(1, 1)
nn.init.constant_(self.linear.weight, 1), nn.init.constant_(self.linear.bias, 0)
def forward(self, x):
return self.linear(x)
net = Net()
torch.save(net.state_dict(), 'savemovel/test_params_model.pkl') #モデルの保存
[OUT]
7-2.学習済みモデルの読み込み:torch.load()
保存方法に合わせて学習済みモデルの読み込みも2種あります。
torch.load(<学習済みモデルのpickleファイルパス>)
モデルのオブジェクトmodelを作成後にstate_dict()を読み込み
重要なポイントとして「学習済みモデルの方でも同じモデルをオブジェクト化しないとエラーが発生」します。

【torch.load(<学習済みモデルのpickleファイルパス>)】
[IN]
import torch
import torch.nn as nn
class Net(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(1, 1)
nn.init.constant_(self.linear.weight, 1), nn.init.constant_(self.linear.bias, 0)
def forward(self, x):
return self.linear(x)
model = torch.load('savemodel/test_model.pkl')
print(model,'\n', model.state_dict())
[OUT]
Net(
(linear): Linear(in_features=1, out_features=1, bias=True)
)
OrderedDict([('linear.weight', tensor([[1.]])), ('linear.bias', tensor([0.]))])【model.load_state_dict(torch.load('model_weight.pth'))】
[IN]
import torch
import torch.nn as nn
class Net(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(1, 1)
nn.init.constant_(self.linear.weight, 1), nn.init.constant_(self.linear.bias, 0)
def forward(self, x):
return self.linear(x)
params_model = torch.load('savemodel/test_params_model.pkl') #モデルパラメータの読み込み
model = Net() #モデルのインスタンス化
model.load_state_dict(params_model) #モデルパラメータの読み込み
print(model,'\n', model.state_dict())
[OUT]
Net(
(linear): Linear(in_features=1, out_features=1, bias=True)
)
OrderedDict([('linear.weight', tensor([[1.]])), ('linear.bias', tensor([0.]))])8.機械学習用の関数・モジュール
8-1.torch.utils
Pytorchで前処理の簡易化ができる機能があります。個人的にはsklearnの方が使いやすい(慣れている)ためそちらを使っています。
8-1-1.データの分割:random_split()
機械学習には過学習を防止するためにデータを学習・検証・テスト用データに分けます。Pytorchではrandam_splitメソッドを使用することで分割でき、多分割も可能です。なお引数のlengthsに分割する数を指定する必要があります。
[IN]
from sklearn import datasets
import torch
import numpy as np
iris = datasets.load_iris()
datas, labels = iris.data, iris.target #data数は150個
num_train = int(len(df) * 0.8) # 80%を訓練データにする
num_val = int(len(df) - num_train) # 残りを検証データにする
train, val = torch.utils.data.random_split(datas, lengths=[num_train, num_val]) # データを分割する
print('trainデータ数:', len(train), 'valデータ数:', len(val))
train, val, test = torch.utils.data.random_split(datas, lengths=[100, 30, 20]) # データを分割する
print('trainデータ数:', len(train), 'valデータ数:', len(val), 'testデータ数:', len(test))
[OUT]
trainデータ数: 120 valデータ数: 30
trainデータ数: 100 valデータ数: 30 testデータ数: 208-1-2.データセットの作成:DataLoader()
実際の学習時はデータ1個ごとで学習するわけではなくミニバッチで学習させます。そのミニバッチを効率的に作成できるクラスとしてDataLoaderがあります。出力値はジェネレーターのためfor文で値を抽出し、各ループでミニバッチのデータが取得できます。
自作のDatasets作成は下記記事に記載しました。
【DataLoaderの引数】
●dataset (Dataset):分割したいデータ
●batch_size (int, optional):ミニバッチ数
●shuffle (bool, optional):ミニバッチのデータをシャッフルするか
●sampler (Sampler or Iterable, optional):-
●batch_sampler (Sampler or Iterable, optional):-
●num_workers (int, optional):-
●collate_fn (callable, optional):-
●pin_memory (bool, optional):-
●drop_last (bool, optional):-
●timeout (numeric, optional):-
●worker_init_fn (callable, optional):-
●generator (torch.Generator, optional):-
●prefetch_factor (int, optional, keyword-only arg):-
●persistent_workers (bool, optional):-
●pin_memory_device (str, optional):-
[IN]
from torch.utils.data import DataLoader
data = DataLoader(datas, batch_size=30, shuffle=True)
print(data)
for i, batch in enumerate(data):
print(i, type(batch), batch.shape)
[OUT]
<torch.utils.data.dataloader.DataLoader object at 0x000001F1C06188B0>
0 <class 'torch.Tensor'> torch.Size([30, 4])
1 <class 'torch.Tensor'> torch.Size([30, 4])
2 <class 'torch.Tensor'> torch.Size([30, 4])
3 <class 'torch.Tensor'> torch.Size([30, 4])
4 <class 'torch.Tensor'> torch.Size([30, 4])より動作が分かるように0-59(60個)の連番をbatch20でシャッフルTrue/Falseで実行してみました。
[IN]
from torch.utils.data import DataLoader
import numpy as np
datas = np.arange(0, 60, 1) #Numpy型[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59]
batchs1, batchs2 = DataLoader(datas, batch_size=20, shuffle=True), DataLoader(datas, batch_size=20, shuffle=False)
print('データセットのデータ(ミニバッチ)数', len(batchs1)) #全60個を20個ずつに分けると3個になる
print('Shuffle: True')
for batch in batchs1:print(batch)
print('Shuffle: False')
for batch in batchs2:print(batch)
[OUT]
データセットのデータ(ミニバッチ)数 3
Shuffle: True
tensor([59, 22, 55, 31, 57, 24, 47, 51, 17, 49, 13, 45, 3, 6, 41, 39, 12, 56,
44, 42], dtype=torch.int32)
tensor([27, 58, 28, 1, 15, 33, 20, 30, 48, 5, 11, 19, 43, 29, 50, 8, 9, 53,
35, 52], dtype=torch.int32)
tensor([25, 18, 46, 14, 54, 21, 32, 16, 0, 40, 4, 37, 23, 38, 7, 34, 2, 26,
36, 10], dtype=torch.int32)
Shuffle: False
tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,
18, 19], dtype=torch.int32)
tensor([20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37,
38, 39], dtype=torch.int32)
tensor([40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57,
58, 59], dtype=torch.int32)9.目的関数(損失関数)
正解値と推定値の正しさを比較(評価)するための関数として目的関数(損失関数)があります。一覧は下記の"Loss Functions"をご確認ください。
通常の流れは①損失関数で誤差lossを計算、②逆伝搬"loss.backward()"で勾配を計算、③optimizer.step()でパラメータ更新をします。
[IN※サンプルコードのため実行するとエラーとなります]
model = <AIモデル>
criterion = <損失関数>
optimiser = <最適化関数 torch.optim>
#下記から通常はループで学習を繰り返す
optimizer.zero_grad() #勾配の初期化
outputs = model(inputs) #推論
loss = criterion(outputs, labels) #誤差計算
loss.backward() #勾配計算
optimizer.step() #パラメータ更新
[OUT]
-9-1.自作関数作成(MSE)+loss.backward()検証
損失関数は自作で作成できます。loss.backward()の動作検証も含めて自分で"平均二乗誤差(MSE)"を作成して動きを確認します。なお勾配の計算そのものは下記記事に詳細を記載しております。
下記コードより①自作の損失関数でもlossの計算が可能、②loss.backward()前は勾配がないが実行後に勾配を取得できる ことが確認できます。
[IN]
import torch
# データの準備
torch.manual_seed(0) #乱数のシードを設定
x = torch.arange(-2, 2.1, 0.25)
y_label = 5*x + torch.randn(len(x))
#パラメーターの設定
w = torch.randn(1, requires_grad=True) #重みを設定:ランダム値Ver.
b = torch.tensor(1.0, requires_grad=True) #バイアスを設定:固定値Ver.
print('重みw情報:', w, w.shape, 'バイアスb情報:' ,b, b.shape)
def pred(x): #予測値を計算する関数
return w*x + b
def mean_squared_error(y_pred, y_label): #損失関数を計算する関数
return ((y_pred - y_label)**2).mean()
y_pred = pred(x) #予測値を計算
loss = mean_squared_error(y_pred, y_label) #平均二乗誤差を計算
print('loss:', loss)
print('loss.backward()前', 'w.grad:', w.grad, 'b.grad:', b.grad)
loss.backward() #勾配を計算
print('loss.backward()後', 'w.grad:', w.grad, 'b.grad:', b.grad)
[OUT]
重みw情報: tensor([0.4154], requires_grad=True) torch.Size([1])
バイアスb情報: tensor(1., requires_grad=True) torch.Size([])
loss: tensor(38.0037, grad_fn=<MeanBackward0>)
loss.backward()前 w.grad: None b.grad: None
loss.backward()後 w.grad: tensor([-14.7817]) b.grad: tensor(1.6475)9-2.Pytorchの損失関数(回帰)
一般的に回帰向けの損失関数(一部のみ)は下記の通りです。
【回帰向けの損失関数一覧】
●nn.MSELoss:平均二乗誤差(Mean Square Error)
●nn.L1Loss:Mean Absolute Error(MAE)->絶対値の差分の平均
$$
MAE=\frac{1}{N}\sum_{i=1}^{N}|y_{pred}-y_{label}|\\
MSE=\frac{1}{N}\sum_{i=1}^{N}(y_{pred}-y_{label})^2
$$
[IN]
import torch
import torch.nn as nn
import numpy as np
y_label = torch.tensor([1.0, 2.0, 3.0, 9.0])
y_pred = torch.tensor([1.0, 1.5, 3.0, -1.0])
diff_y = y_label - y_pred
print(diff_y, diff_y**2)
print((diff_y**2).mean(), diff_y.mean()) #事前確認
criterion_MSE = nn.MSELoss()
criterion_L1 = nn.L1Loss()
loss_MSE = criterion_MSE(y_pred, y_label)
loss_L1 = criterion_L1(y_pred, y_label)
print('MSE:', loss_MSE, 'L1:', loss_L1)
[OUT]
tensor([ 0.0000, 0.5000, 0.0000, 10.0000]) tensor([ 0.0000, 0.2500, 0.0000, 100.0000])
tensor(25.0625) tensor(2.6250)
MSE: tensor(25.0625) L1: tensor(2.6250)9-3.Pytorchの損失関数(分類)
一般的に分類向けの損失関数(一部のみ)は下記の通りです。
【分類向けの損失関数一覧】
●nn.LogSoftmax:softmaxで確率pを計算後にlog(p)にする
->本節に記載したがLogSoftmaxは損失関数ではないことに注意
->合計値は1にならないため確率としても使用できない
●nn.NLLLoss:Negative Log Likelihood Lossの略
->①ラベルから正解のindex取得、②該当indexの入力値を取得、③-1をかける、④全データ(全行)の平均値を算出する
->入力値がnn.Logsoftmaxによる確率log(p)の場合、"全行の-log(p)平均値"になるためnn.CrossEntropyLossと同じ動作になる
●nn.BCELOSS:2値分類の公差エントロピー
->データの渡し方はloss(<予測値(確率)>,<ラベル(カテゴリカル)>)
※逆にするとエラーになる
-> Binary Cross Entropyの略
●nn.CrossEntropyLoss:交差エントロピー
->nn.LogSoftmaxとnn.NLLLossの組み合わせと同等
->データの渡し方はloss(<予測値(確率)>,<ラベル(カテゴリカル)>)
※逆にするとエラーになる
$$
BCE(2値分類) = -{(y\log(p) + (1 - y)\log(1 - p))}
$$
$$
CrossEntropy(多値値分類) = -\sum_{c=1}^My_{o,c}\log(p_{o,c})
$$
M:クラス数, log:自然対数, y:正解ラベル (0 or 1), p:推定クラスの確率(推論値)
【nn.BCELOSS(Binary Cross Entropy)の動作確認】
[IN]
import torch
import torch.nn as nn
import numpy as np
y_label = torch.tensor([0.0, 0.0, 0.0, 1.0, 1.0]) #正解ラベルもfloat型にする
y_pred = torch.tensor([0.99, 0.5, 0.99, 0.5, 0.99])
criterion_BCE = nn.BCELoss() #Binary Cross Entropy Loss
loss_BCE = criterion_BCE(y_pred, y_label)
loss_BCE
[OUT]
tensor(2.1213)【参考※答え合わせ】

【nn.LogSoftmaxの動作確認】
●dim=1を指定することで行方向に計算する
[IN]
torch.manual_seed(0) #乱数シードを固定
input = torch.randn(3, 5, requires_grad=True)
print(input)
m = nn.LogSoftmax(dim=1) #dim=1で行方向に計算
m(input)
[OUT]
tensor([[ 1.5410, -0.2934, -2.1788, 0.5684, -1.0845],
[-1.3986, 0.4033, 0.8380, -0.7193, -0.4033],
[-0.5966, 0.1820, -0.8567, 1.1006, -1.0712]], requires_grad=True)
tensor([[-0.4913, -2.3257, -4.2111, -1.4639, -3.1168],
[-3.0493, -1.2474, -0.8127, -2.3700, -2.0541],
[-2.3056, -1.5270, -2.5657, -0.6084, -2.7802]],
grad_fn=<LogSoftmaxBackward>)
【nn.NLLLOSSの動作確認】
●「nn.LogSoftmaxとnn.NLLLOSS」=nn.CrossEntropyLossである。
●単純に-1をかけて平均するだけのシンプルな損失関数
[IN]
i = torch.tensor([[1,2,3],
[4,5,6],
[7,8,9]]).float()
t = torch.tensor([0, 1, 2]).long()
loss_NLL(i, t) #-1-5-9の平均(=-5)
[OUT]
tensor(-5.)[IN]
torch.manual_seed(0) #乱数シードを固定
input = torch.randn(3, 5, requires_grad=True)
target = torch.empty(3, dtype=torch.long).random_(5) #torch.Size([3])
print(input)
print(target)
m = nn.LogSoftmax(dim=1) #dim=1で行方向に計算
loss_NLL = nn.NLLLoss() #Negative Log Likelihood Loss
m(input)
print(loss_NLL(m(input), target))
[OUT]
tensor([[ 1.5410, -0.2934, -2.1788, 0.5684, -1.0845],
[-1.3986, 0.4033, 0.8380, -0.7193, -0.4033],
[-0.5966, 0.1820, -0.8567, 1.1006, -1.0712]], requires_grad=True)
tensor([3, 0, 0])
tensor(2.2729, grad_fn=<NllLossBackward>)
【nn.CrossEntropyLoss(多値公差エントロピー)の動作確認】
●各データ(行)でsoftmaxを計算するため行の合計は1
●ラベルのindexに該当するデータのみ、確率pから-log(p)で算出
[IN]
torch.manual_seed(0) #乱数シードを固定
loss = nn.CrossEntropyLoss()
input = torch.randn(3, 5, requires_grad=True) #torch.Size([3, 5])
target = torch.empty(3, dtype=torch.long).random_(5) #torch.Size([3])
print(input)
print(target)
print('loss', loss(input, target))
[OUT]
tensor([[ 1.5410, -0.2934, -2.1788, 0.5684, -1.0845],
[-1.3986, 0.4033, 0.8380, -0.7193, -0.4033],
[-0.5966, 0.1820, -0.8567, 1.1006, -1.0712]], requires_grad=True)
tensor([3, 0, 0])
loss tensor(2.2729, grad_fn=<NllLossBackward>)
10.最適化関数:torch.optim
損失関数で計算した誤差lossから効率よくパラメータ(重みw, バイアスb)へ勾配の値を渡して更新する関数としてtorch.optimがあります。一般的なアルゴリズムを一覧で記載しましたが、他のものは下記の"Algorithms"をご確認ください。
【最適化関数】
●optim.SGD(params, lr):確率的勾配降下法(SGD)
->最もシンプルで理解しやすくそこそこよい動きをする
->関数の形状が等方的でないと非効率な経路で探索する欠点がある
●optim.SGD(params, lr, momentum):Momentum
->モデルはSGDと同じAPIを使用する
->SGDの欠点を改善するためパラメータ更新時に更新用パラメータがある
->過学習対策としての" weight decay"も設定可能
●optim.Adagrad:AdaGrad
->学習率ηを学習が進む(epoch数が増える)に連れて小さくする(最初は大きく学習して、後の方で小さく学習させる)仕組みがある
●optim.Adam:Adam(2015年に提案)
->MomentumとAdaGradを融合したようなもの
一般的な最適化関数の使用フローは下記の通りですが、本記事では勉強用としてスクラッチでの作成も紹介します。
torch.optimで最適化関数のオブジェクト作成:この時に学習時に更新したいパラメータを渡す(後でoptimizer.step()でパラメータ更新するため)
"optimizer.zero_grad()"でパラメータの勾配を初期化(値=0)にする
損失関数で計算したlossをloss.backward()して、"optimizer.step()"でパラメータを更新する。
[IN※サンプルコードのため実行するとエラーとなります]
model = <AIモデル>
criterion = <損失関数>
optimiser = <最適化関数 torch.optim>
#下記から通常はループで学習を繰り返す
optimizer.zero_grad() #勾配の初期化
outputs = model(inputs) #推論
loss = criterion(outputs, labels) #誤差計算
loss.backward() #勾配計算
optimizer.step() #パラメータ更新
[OUT]
-10-1.Optimizerのメソッド一覧
生成したOptimizerは下記のメソッドを持ちます。
【Optimizerのメソッド一覧】
●Optimizer.add_param_group:param group?を追加する
●Optimizer.load_state_dict:optimizerの状態を読み込む
●Optimizer.state_dict:optimizerの状態をdictで出力
●Optimizer.step:(optimizerに渡した)パラメータを更新する
●Optimizer.zero_grad:勾配を0にする(最適化した全torch.Tensorを0にする)
10-2.学習用_SGDを0から作成:torch.no_grad()
理解を深めるためにまずはSGDをスクラッチで作成します。なお通常ではこの記法は使用しない(torch.optimを使用する)ためあくまで学習用です。
スクラッチでの処理フローは下記の通りです。
手順としては①損失loss計算、②loss.backward()で勾配を計算、③学習率η×勾配を今のパラメータに更新、④勾配の初期化 である。
勾配を持ったままパラメータ更新できないため"with torch.no_grad()"をつけて更新する
各変数の勾配初期化は"tensor.grad.zero_()"を使用する。
$$
W ← W - η\frac{\partial Loss}{\partial W}
$$
$$
b ← b - η\frac{\partial Loss}{\partial b}
$$
[IN※エラー例]
w -= lr * w.grad
b -= lr * b.grad
[OUT]
RuntimeError: a leaf Variable that requires grad is being used in an in-place operation.動作確認用のコードは下記の通りです。下記より①torch.no_grad()をつけることでエラーなくパラメータ更新ができる、②grad.zero_()で勾配を初期化できた ことを確認できました。
[IN]
import torch
# データの準備
torch.manual_seed(0) #乱数のシードを設定
x = torch.arange(-2, 2.1, 0.25)
y_label = 5*x + torch.randn(len(x))
#パラメーターの設定
w = torch.randn(1, requires_grad=True) #重みを設定:ランダム値Ver.
b = torch.tensor(1.0, requires_grad=True) #バイアスを設定:固定値Ver.
def pred(x): #予測値を計算する関数
return w*x + b
def mean_squared_error(y_pred, y_label): #損失関数を計算する関数
return ((y_pred - y_label)**2).mean()
y_pred = pred(x) #予測値を計算
loss = mean_squared_error(y_pred, y_label) #平均二乗誤差を計算
loss.backward() #勾配を計算
lr = 0.01 #学習率
with torch.no_grad():
print('更新前_', 'w:', w, 'b:', b)
w -= lr * w.grad #重みを更新
b -= lr * b.grad #重みを更新
print('更新後_', 'w:', w, 'b:', b)
print('w.grad.zero_()前', w.grad, b.grad)
w.grad.zero_() #勾配を初期化
b.grad.zero_() #勾配を初期化
print('w.grad.zero_()後', w.grad, b.grad)
[OUT]
更新前_ w: tensor([0.4154], requires_grad=True) b: tensor(1., requires_grad=True)
更新後_ w: tensor([0.5632], requires_grad=True) b: tensor(0.9835, requires_grad=True)
w.grad.zero_()前 tensor([-14.7817]) tensor(1.6475)
w.grad.zero_()後 tensor([0.]) tensor(0.)【参考1:毎回勾配を初期化する理由】
毎回勾配を初期化する理由として「Pytorchでは勾配情報は自動で初期化されずloss.backward()毎に勾配が積算される」ためです。
下記に初期化せずに2回勾配計算を行いました。通常では更新ごとに勾配は小さくなるはずですが、ほぼ2倍の値が出ております。これは勾配が積算されているためであり、初期化しないとパラメータ更新時に過剰な更新が生じることが分かります。
[IN]
import torch.nn as nn
lr = 0.01 #学習率
nn.init.constant_(w, 0.4154), nn.init.constant_(b, 1.0), #重みを初期化
w.grad.zero_(), b.grad.zero_() #勾配を初期化※重みを初期化しても勾配は初期化されないので注意
y_pred = pred(x) #予測値を計算
loss = mean_squared_error(y_pred, y_label) #平均二乗誤差を計算
loss.backward() #勾配を計算
with torch.no_grad():
print('更新前_', 'w:', w, 'b:', b)
w -= lr * w.grad #重みを更新
b -= lr * b.grad #重みを更新
print('更新後_', 'w:', w, 'b:', b)
print('w.grad:', w.grad, 'b.grad:', b.grad, end='\n\n')
y_pred2 = pred(x) #予測値を計算
loss = mean_squared_error(y_pred2, y_label) #平均二乗誤差を計算
loss.backward() #勾配を計算
with torch.no_grad():
print('更新前_', 'w:', w, 'b:', b)
w -= lr * w.grad #重みを更新
b -= lr * b.grad #重みを更新
print('更新後_', 'w:', w, 'b:', b)
print('w.grad:', w.grad, 'b.grad:', b.grad)
[OUT]
更新前_ w: tensor([0.4154], requires_grad=True) b: tensor(1., requires_grad=True)
更新後_ w: tensor([0.5632], requires_grad=True) b: tensor(0.9835, requires_grad=True)
w.grad: tensor([-14.7816]) b.grad: tensor(1.6475)
更新前_ w: tensor([0.5632], requires_grad=True) b: tensor(0.9835, requires_grad=True)
更新後_ w: tensor([0.8544], requires_grad=True) b: tensor(0.9509, requires_grad=True)
w.grad: tensor([-29.1197]) b.grad: tensor(3.2620)【参考2:手動Ver.での完成コード】
torch.optimを使用するため通常では下記コードは使用しませんが、更新まで含めた完成コードは下記の通りです。
[IN]
import torch
import pandas as pd
# データの準備
torch.manual_seed(0) #乱数のシードを設定
x = torch.arange(-2, 2.1, 0.25)
y_label = 5*x + torch.randn(len(x))
#パラメーターの設定
w = torch.randn(1, requires_grad=True) #重みを設定:ランダム値Ver.
b = torch.tensor(1.0, requires_grad=True) #バイアスを設定:固定値Ver.
print(w,b)
def pred(x): #予測値を計算する関数
return w*x + b
def mean_squared_error(y_pred, y_label): #損失関数を計算する関数
return ((y_pred - y_label)**2).mean()
y_pred = pred(x) #予測値を計算
loss = mean_squared_error(y_pred, y_label) #平均二乗誤差を計算
loss.backward() #勾配を計算
epochs = 120 #学習回数
lr = 0.01 #学習率
logs = {'epoch':[], 'wight':[], 'bias':[], 'loss':[]} #学習結果を格納する辞書
for epoch in range(epochs+1):
y_pred = pred(x) #予測値を計算
loss = mean_squared_error(y_pred, y_label) #平均二乗誤差を計算
loss.backward() #勾配を計算
with torch.no_grad():
w -= lr * w.grad #重みを更新
b -= lr * b.grad #バイアスを更新
#勾配の初期化
w.grad.zero_()
b.grad.zero_()
if epoch%10 == 0:
logs['epoch'].append(epoch) #学習回数を格納
logs['wight'].append(w.item()) #重みを格納
logs['bias'].append(b.item()) #バイアスを格納
logs['loss'].append(loss.item()) #損失関数を格納
print(f'重みw:{w.item():.2f}, バイアスb:{b.item():.3f}, loss:{loss.item():.3f}')
df = pd.DataFrame(logs).T
df
[OUT]
tensor([0.4154], requires_grad=True)
tensor(1., requires_grad=True)
重みw:5.22, バイアスb:0.246, loss:0.937
10-3.torch.optimの使用方法(コード編)
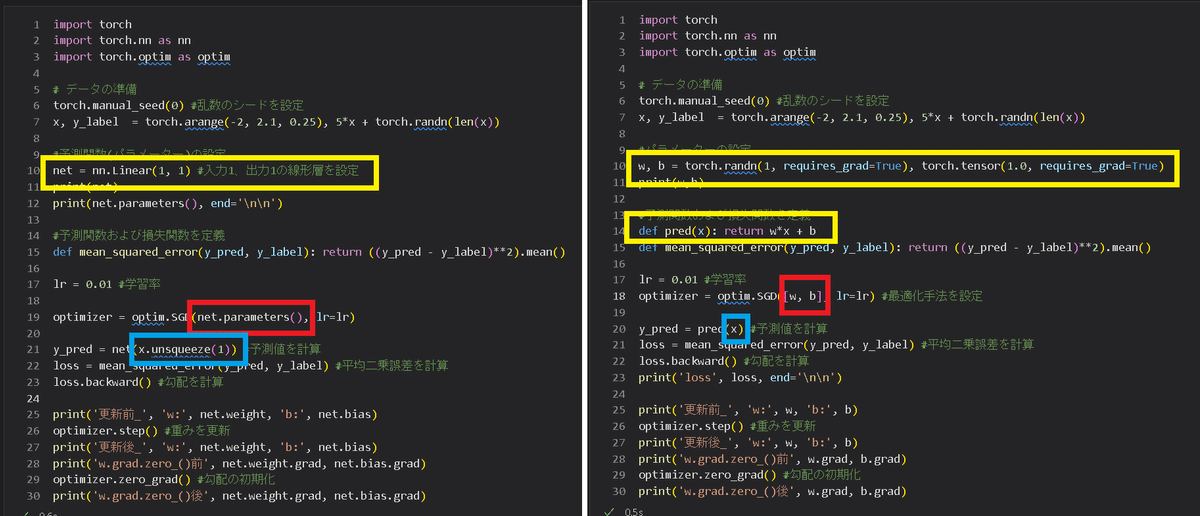
スクラッチVer.では各テンソルの勾配更新/初期化+(最適化モデル)を実施しましたが、torch.optimを使用することで簡易化できます。コードの比較は下図の通りであり、optimizerオブジェクトですべて実施できます。

[IN]
import torch
import torch.nn as nn
import torch.optim as optim
# データの準備
torch.manual_seed(0) #乱数のシードを設定
x = torch.arange(-2, 2.1, 0.25)
y_label = 5*x + torch.randn(len(x))
#パラメーターの設定
w, b = torch.randn(1, requires_grad=True), torch.tensor(1.0, requires_grad=True)
print(w,b)
#予測関数および損失関数を定義
def pred(x): return w*x + b
def mean_squared_error(y_pred, y_label): return ((y_pred - y_label)**2).mean()
lr = 0.01 #学習率
# optimizer = optim.SGD([w, b], lr=lr) #最適化手法を設定
optimizer = optim.SGD([w, b], lr=lr)
y_pred = pred(x) #予測値を計算
loss = mean_squared_error(y_pred, y_label) #平均二乗誤差を計算
loss.backward() #勾配を計算
print('loss', loss, end='\n\n')
print('更新前_', 'w:', w, 'b:', b)
optimizer.step() #重みを更新
print('更新後_', 'w:', w, 'b:', b)
print('w.grad.zero_()前', w.grad, b.grad)
optimizer.zero_grad() #勾配の初期化
print('w.grad.zero_()後', w.grad, b.grad)
[OUT]
tensor([0.4154], requires_grad=True)
tensor(1., requires_grad=True)
loss tensor(38.0037, grad_fn=<MeanBackward0>)
更新前_ w: tensor([0.4154], requires_grad=True) b: tensor(1., requires_grad=True)
更新後_ w: tensor([0.5632], requires_grad=True) b: tensor(0.9835, requires_grad=True)
w.grad.zero_()前 tensor([-14.7817]) tensor(1.6475)
w.grad.zero_()後 tensor([0.]) tensor(0.) なお上記では" optim.SGD([w, b], lr=lr)"のようにリスト形式でパラメータを渡しましたが直近の最新AIモデルは大量(GPT-3は1750億)のパラメータがあるためこの方法が現実的ではありません。
ここで重要なのが前章で作成した"torch.nn"です。"torch.nn"で作成したモデルは"paramters()"の中に全パラメータをジェネレーター形式で保持してます。このparameters()を渡すことでパラメータ更新が可能です。
[IN]
import torch
import torch.nn as nn
import torch.optim as optim
# データの準備
torch.manual_seed(0) #乱数のシードを設定
x = torch.arange(-2, 2.1, 0.25)
y_label = 5*x + torch.randn(len(x))
x.unsqueeze_(1) #xを2次元テンソルに変換:torch.Size([17])->torch.Size([17, 1])
#予測関数(パラメーター)の設定
net = nn.Linear(1, 1) #入力1、出力1の線形層を設定
print(net)
print(net.parameters(), end='\n\n')
#予測関数および損失関数を定義
def mean_squared_error(y_pred, y_label): return ((y_pred - y_label)**2).mean()
lr = 0.01 #学習率
optimizer = optim.SGD(net.parameters(), lr=lr)
y_pred = net(x) #予測値を計算
loss = mean_squared_error(y_pred, y_label) #平均二乗誤差を計算
loss.backward() #勾配を計算
print('更新前_', 'w:', net.weight, 'b:', net.bias)
optimizer.step() #重みを更新
print('更新後_', 'w:', net.weight, 'b:', net.bias)
print('w.grad.zero_()前', net.weight.grad, net.bias.grad)
optimizer.zero_grad() #勾配の初期化
print('w.grad.zero_()後', net.weight.grad, net.bias.grad)
[OUT]
Linear(in_features=1, out_features=1, bias=True)
<generator object Module.parameters at 0x000001A892DEFF90>
更新前_ w: Parameter containing:
tensor([[-0.4603]], requires_grad=True) b: Parameter containing:
tensor([-0.6986], requires_grad=True)
更新後_ w: Parameter containing:
tensor([[-0.4465]], requires_grad=True) b: Parameter containing:
tensor([-0.6811], requires_grad=True)
w.grad.zero_()前 tensor([[-1.3810]]) tensor([-1.7498])
w.grad.zero_()後 tensor([[0.]]) tensor([0.])11.可視化・確認用モジュール
11ー1.モデルのサマリー:torchinfo.summary
モデルのサマリー表示はtorchinfoモジュールのsummaryを使用します。
[IN]
import torch
import torch.nn as nn
from torchinfo import summary
model = nn.Linear(1, 1) #入力1、出力1の線形層(wx+b)を作成
summary(model, input_size=(1, ))
[OUT]
==========================================================================================
Layer (type:depth-idx) Output Shape Param #
==========================================================================================
Linear [1] 2
==========================================================================================
Total params: 2
Trainable params: 2
Non-trainable params: 0
Total mult-adds (M): 0.00
==========================================================================================
Input size (MB): 0.00
Forward/backward pass size (MB): 0.00
Params size (MB): 0.00
Estimated Total Size (MB): 0.00
==========================================================================================11-2.計算グラフの表示:make_dot
計算グラフの作成はtorchvizライブラリのmake_dotで実施します。
[IN]
import torch
from torchviz import make_dot
# データの準備
x = torch.arange(-2, 2.1, 0.25)
y_label = 5*x + torch.randn(len(x))
#パラメーターの設定
w, b = torch.randn(1, requires_grad=True), torch.tensor(1.0, requires_grad=True)
#予測関数および損失関数を定義
def pred(x): return w*x + b
def mean_squared_error(y_pred, y_label): return ((y_pred - y_label)**2).mean()
y_pred = pred(x) #予測値を計算
loss = mean_squared_error(y_pred, y_label) #平均二乗誤差を計算
g = make_dot(loss, params={'w':w, 'b':b})
display(g)
[OUT]
()内の数値はパラメータ数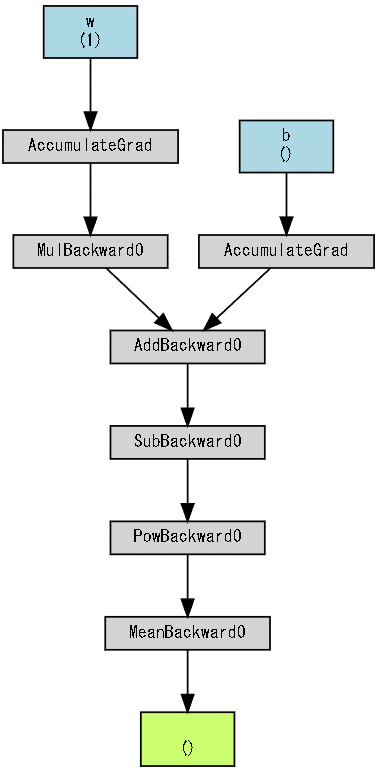
12.複数の形で線形モデル(y=wx+b)を作成
参考として下記パターン化で線形モデルを作成してみました。なお線形モデルにおけるPytorchの動作検証に関しては下記記事をご確認ください。
スクラッチ(自作)
torch.nnによるnn.Linear()から作成
nn.Moduleによるカスタムクラスから作成
12-1.推論モデル(順伝搬)の作成
各パターンでの順伝搬の作成は下記の通りです。Pytorchでは行列計算を実行するため1次元の線形モデルでも入力値は2次元(N, 1)にする必要があり、出力も(N,1)となります。
[IN]
import torch
import torch.nn as nn #パラメータをもつレイヤ関数
import torch.nn.functional as F #パラメータをもたないレイヤ関数
# データの準備
torch.manual_seed(0) #乱数のシードを設定
x = torch.tensor([1, 2, 3]).float()
y_label = 5*x + torch.randn(len(x))
print('x=', x, 'y=', y_label, end='\n\n')
x_2dim = x.unsqueeze(1) #xを2次元テンソルに変換:torch.Size([17])->torch.Size([17, 1])
#スクラッチで作成
w, b = torch.tensor(1.5410, requires_grad=True), torch.tensor(1.0, requires_grad=True)
def pred(x): return w*x + b
print(pred(x), end='\n\n')
#nn.Linear()から作成
linear = nn.Linear(1, 1) #入力1、出力1の線形層(wx+b)を作成
linear.weight.data.fill_(1.5410), linear.bias.data.fill_(1.0) #重みを初期化
print(linear(x_2dim), end='\n\n')
#nn.Moduleクラスから作成
class Net(nn.Module):
def __init__(self, n_in, n_out):
super().__init__() #nn.Moduleの継承(初期化呼び出し)
#レイヤの定義
self.f1 = nn.Linear(n_in, n_out) #入力層:n_in, 出力層:n_outの線形レイヤ
#重みの初期化
nn.init.constant_(self.f1.weight, 1.5410), nn.init.constant_(self.f1.bias, 1.0)
def forward(self, x):
out = self.f1(x)
return out
net = Net(1,1)
print(net(x_2dim))
[OUT]
x= tensor([1., 2., 3.]) y= tensor([ 6.5410, 9.7066, 12.8212])
tensor([2.5410, 4.0820, 5.6230], grad_fn=<AddBackward0>)
tensor([[2.5410],
[4.0820],
[5.6230]], grad_fn=<AddmmBackward>)
tensor([[2.5410],
[4.0820],
[5.6230]], grad_fn=<AddmmBackward>)12-2.学習フェーズ(逆伝搬)の作成
それぞれの学習フェーズを記載しますが一連の流れはすべて同じです。
(線形)モデルを使用して推論値を計算する
損失関数を使用して"正解値"と"推論値"から誤差を求める
loss.backward()で各パラメータの勾配を求める
optimizer.step()(または手動)によりパラメータを更新する
zero_grad()によりパラメータの勾配を初期化する
1~5をループ計算する
事前に学習用の係数は下記の通り作成しておきます。なおうまく学習出来たら正解値はw=3.14, b=3.41になります。
[IN]
import pandas as pd
#学習用パラメータ・変数
epochs = 200 #学習回数
lr = 0.01 #学習率
def logging_epoch(logs, epoch, w, b, loss): #学習結果を辞書に格納する関数
logs['epoch'].append(epoch) #学習回数を格納
logs['wight'].append(w) #重みを格納
logs['bias'].append(b) #バイアスを格納
logs['loss'].append(loss) #損失関数を格納
torch.manual_seed(0)【スクラッチVer.】
結果として(何故か)ちゃんと学習出来ています。
[IN]
#逆伝搬:スクラッチで作成
def mean_squared_error(y_pred, y_label): return ((y_pred - y_label)**2).mean() #損失関数
logs = {'epoch':[], 'wight':[], 'bias':[], 'loss':[]} #学習結果を格納する辞書
for epoch in range(epochs+1):
y_pred = pred(x) #順伝搬:予測値を計算
loss = mean_squared_error(y_pred, y_label) #損失を計算
loss.backward() #逆伝搬:勾配を計算
with torch.no_grad():
w -= lr * w.grad #重みを更新
b -= lr * b.grad #バイアスを更新
#勾配の初期化
w.grad.zero_(), b.grad.zero_()
if epoch%10 == 0:
logging_epoch(epoch=epoch, w=w.item(), b=b.item(), loss=loss.item())
print(f'重みw:{w.item():.2f}, バイアスb:{b.item():.2f}, loss:{loss.item():.3f}')
display(pd.DataFrame(logs).T)
[OUT]
重みw:3.14, バイアスb:3.41, loss:0.000
【nn.Linear() ver.】
今回は数値が確認しやすいように入力値xを正規化していないため途中で学習が頭打ちになっています。(何故スクラッチではうまくいったかは不明)
[IN]
#学習用パラメータ・変数
optimizer = torch.optim.SGD(linear.parameters(), lr=lr) #最適化手法を定義:SGD(確率的勾配降下法)
critertion = nn.MSELoss() #損失関数を定義:平均二乗誤差
logs2 = {'epoch':[], 'wight':[], 'bias':[], 'loss':[]} #学習結果を格納する辞書
for epoch in range(epochs+1):
y_pred = linear(x_2dim) #順伝搬:予測値を計算
loss = mean_squared_error(y_pred, y_label) #損失を計算
loss.backward() #逆伝搬:勾配を計算
optimizer.step() #重みを更新
optimizer.zero_grad() #勾配の初期化
if epoch%10 == 0:
logging_epoch(logs=logs2, epoch=epoch, w=linear.weight.item(), b=linear.bias.item(), loss=loss.item())
print(f'重みw:{linear.weight.item():.2f}, バイアスb:{linear.bias.item():.2f}, loss:{loss.item():.3f}')
display(pd.DataFrame(logs2).T)
[OUT]
重みw:2.13, バイアスb:4.85, loss:9.948
【nn.Moduleによるカスタムクラス ver.】
基本的にnn.linear()のオブジェクトをnn.Module()のものに置き換えるだけです。なお" optimizer.zero_grad()"は optimizer.step()の後でも問題ないですが、残留している勾配を流さないように先に持ってきました。
[IN]
optimizer = torch.optim.SGD(net.parameters(), lr=lr) #最適化手法を定義:SGD(確率的勾配降下法)
critertion = nn.MSELoss() #損失関数を定義:平均二乗誤差
logs3 = {'epoch':[], 'wight':[], 'bias':[], 'loss':[]} #学習結果を格納する辞書
w_net, b_net = [i for i in net.parameters()]
for epoch in range(epochs+1):
optimizer.zero_grad() #勾配の初期化
y_pred = net(x_2dim) #順伝搬:予測値を計算
loss = mean_squared_error(y_pred, y_label) #損失を計算
loss.backward() #逆伝搬:勾配を計算
optimizer.step() #重みを更新
if epoch%10 == 0:
logging_epoch(logs=logs3, epoch=epoch, w=w_net.item(), b=b_net.item(), loss=loss.item())
print(f'重みw:{w_net.item():.2f}, バイアスb:{b_net.item():.2f}, loss:{loss.item():.3f}')
display(pd.DataFrame(logs3).T)
[OUT]
重みw:2.13, バイアスb:4.85, loss:9.948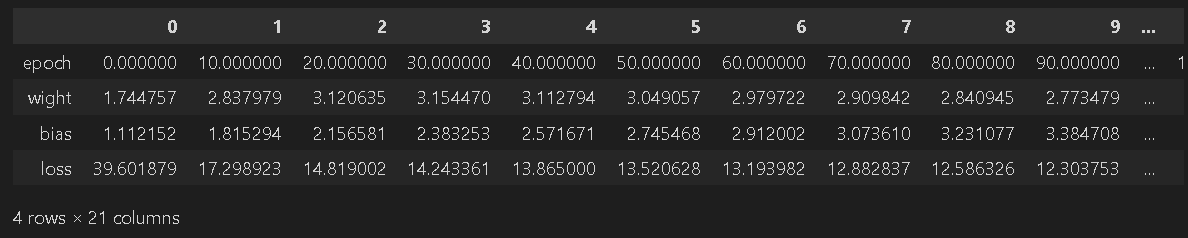
13.完成コード
自分が使いそうな形で完成コードを残しておきますが、おそらく後で編集していく予定です。
13-1.コードメモ
コードのメモは下記の通り。
Pytorchモデルを使用するならデータは最初からtorch.tensor()にしておく。
複雑なモデルにするならデータは大量に用意すること
通常は特徴量エンジニアリングの効果が大きいため、前処理はしっかりすること(今回は時間がないので無視)
前処理で正規化は忘れないこと
学習時はnet.train(), 検証時はnet.eval()でモードを変更すること
13-2.サンプルコード
サンプルコードは下記の通り。比較対象として決定木(最適化なし)を作成
【データセット、前処理、決定木】
[IN]
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchinfo import summary
from tqdm import tqdm
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
from sklearn.tree import DecisionTreeClassifier
#データの読み込み
diamonds = sns.load_dataset("diamonds") # データセットの読み込み
print(type(diamonds), diamonds.shape)
pd.DataFrame(diamonds.isnull().sum(), columns=['欠損値']).T #欠損値の確認
datas, labels = diamonds.drop(columns=['price']), diamonds['price'] # データとラベルに分割
#前処理
datas = pd.get_dummies(datas) # カテゴリ変数をダミー変数に変換
scaler = MinMaxScaler() # スケーリング
scaler.fit(datas) # スケーリングの設定
datas_scale = scaler.transform(datas) #正規化->numpy配列になる
# display(pd.DataFrame(datas_scale, columns=datas.columns)) # 正規化されたデータの確認
x_train, x_test, y_train, y_test = train_test_split(datas_scale, labels, test_size=0.2, random_state=0) # データの分割
print('x_train:', x_train.shape, type(x_train), 'x_test:', x_test.shape, type(x_test)) # データの形状の確認
print('y_train:', y_train.shape, type(y_train), 'y_test:', y_test.shape, type(y_test)) # データの形状の確認
#関数の定義
# criterion = nn.MSELoss() # 損失関数の定義
#参考用モデルSVM
tree = DecisionTreeClassifier(random_state=0)
tree.fit(x_train, y_train) # 学習
y_pred = tree.predict(x_test) # 予測
loss_train = mean_squared_error(y_train, tree.predict(x_train)) # 訓練データの損失
loss_test = mean_squared_error(y_test, y_pred) # MSEの計算
print(f'学習時:loss={loss_train:,.0f}, r2Score(決定係数)={tree.score(x_train, y_train):.3f}') # 損失の表示
print(f'テスト時:loss={loss_test:,.0f}, r2Score(決定係数)={tree.score(x_test, y_test):.3f}') # 損失の表示
print(tree.get_params())
[OUT]
<class 'pandas.core.frame.DataFrame'> (53940, 10)
x_train: (43152, 26) <class 'numpy.ndarray'> x_test: (10788, 26) <class 'numpy.ndarray'>
y_train: (43152,) <class 'pandas.core.series.Series'> y_test: (10788,) <class 'pandas.core.series.Series'>
学習時:loss=143, r2Score(決定係数)=0.997
テスト時:loss=1,256,940, r2Score(決定係数)=0.158
{'ccp_alpha': 0.0, 'class_weight': None, 'criterion': 'gini', 'max_depth': None, 'max_features': None, 'max_leaf_nodes': None, 'min_impurity_decrease': 0.0, 'min_impurity_split': None, 'min_samples_leaf': 1, 'min_samples_split': 2, 'min_weight_fraction_leaf': 0.0, 'random_state': 0, 'splitter': 'best'}【前処理(tensorへ変換)、CUDA設定、全結合モデル作成】
[IN]
class Net(nn.Module):
def __init__(self, n_in, n_out):
super().__init__() # 親クラスの初期化
self.fc1 = nn.Linear(n_in, 128) # 入力層から中間層への線形変換
self.dropout1 = nn.Dropout(p=0.1) # ドロップアウト pが0.1なら10%の確率でドロップ
self.relu1 = nn.ReLU(inplace=True) # 活性化関数:ReLU
self.fc2 = nn.Linear(128, 64) # 中間層から中間層への線形変換
self.relu2 = nn.ReLU(inplace=True) # 活性化関数:ReLU
self.fc3 = nn.Linear(64, n_out)
def forward(self, x):
out = self.fc1(x) # 入力層から中間層への線形変換
out = self.relu1(out) # 活性化関数:ReLU
out = self.dropout1(out) # ドロップアウト
out = self.fc2(out)
out = self.relu2(out) # 活性化関数:ReLU
out = self.fc3(out)
return out
#GPUの設定
device = "cuda" if torch.cuda.is_available() else "cpu"
#データをtensorに変換
x_train_t, x_test_t = torch.tensor(x_train, dtype=torch.float32), torch.tensor(x_test, dtype=torch.float32)
y_train_t, y_test_t = torch.tensor(y_train.to_numpy(), dtype=torch.float32).unsqueeze(1), torch.tensor(y_test.to_numpy(), dtype=torch.float32).unsqueeze(1)
print('x_train:', x_train_t.shape, type(x_train_t), 'x_test:', x_test_t.shape, type(x_test_t)) # データの形状の確認
print('y_train:', y_train_t.shape, type(y_train_t), 'y_test:', y_test_t.shape, type(y_test_t)) # データの形状の確認
#パラメータの設定
torch.manual_seed(0) #乱数のシードを固定
epochs = 1000 #学習回数
lr = 0.01 #学習率
def logging_epoch(logs, epoch, loss): #学習結果を辞書に格納する関数
logs['epoch'].append(epoch) #学習回数を格納
logs['loss'].append(loss) #損失関数を格納
logs = {'train':{'epoch':[], 'loss':[]},
'test':{'epoch':[], 'loss':[]}} #学習結果を格納する辞書
#モデルの定義
net = Net(n_in=x_train.shape[1], n_out=1) # モデルの定義
optimizer = optim.Adam(net.parameters(), lr=lr) # 最適化手法の定義
criterion = nn.MSELoss() # 損失関数の定義
#GPUへ転送
x_train_t, x_test_t, y_train_t, y_test_t = x_train_t.to(device), x_test_t.to(device), y_train_t.to(device), y_test_t.to(device) # GPUへ転送
net= net.to(device) # モデルをGPUへ転送
for epoch in tqdm(range(epochs)):
for phase in ['train', 'val']:
if phase == 'train':
net.train() # モデルを訓練モードに
else:
net.eval() # モデルを評価モードに
optimizer.zero_grad() # 勾配の初期化
if phase == 'train':
output = net(x_train_t) # モデルの出力
loss = criterion(y_train_t, output) # 損失の計算
loss.backward() # 勾配の計算
optimizer.step() # パラメータの更新
if epoch % 10 ==0:
if phase == 'train':
logging_epoch(logs=logs['train'], epoch=epoch, loss=loss.item()) # 学習データの結果を格納
elif phase == 'val':
y_pred_test = net(x_test_t) # テストデータの予測
loss_test = criterion(y_test_t, y_pred_test) # テストデータの損失
logging_epoch(logs=logs['test'], epoch=epoch, loss=loss_test.item()) # テストデータの結果を格納
[OUT]
x_train: torch.Size([43152, 26]) <class 'torch.Tensor'> x_test: torch.Size([10788, 26]) <class 'torch.Tensor'>
y_train: torch.Size([43152, 1]) <class 'torch.Tensor'> y_test: torch.Size([10788, 1]) <class 'torch.Tensor'>[IN]
summary_model = summary(net, (x_train.shape[1],)) # モデルの概要を表示
print(summary_model)
#学習時・検証時の損失の推移を可視化
fig, ax = plt.subplots(1, 1, figsize=(8, 6))
ax.plot(logs['train']['epoch'], logs['train']['loss'],
label='train', color='blue', linewidth=1, alpha=0.5, linestyle='--')
ax.plot(logs['test']['epoch'], logs['test']['loss'],
label='test', color='red', linewidth=1, alpha=0.5, linestyle='-')
plt.grid(), plt.legend()
loss_train = mean_squared_error(y_train_t.cpu().detach().numpy(), net(x_train_t).cpu().detach().numpy()) # 訓練データの損失
loss_test = mean_squared_error(y_test_t.cpu().detach().numpy(), net(x_test_t).cpu().detach().numpy()) # MSEの計算
r2score_train = r2_score(y_train_t.cpu().detach().numpy(), net(x_train_t).cpu().detach().numpy()) # 決定係数の計算
r2score_test = r2_score(y_test_t.cpu().detach().numpy(), net(x_test_t).cpu().detach().numpy()) # 決定係数の計算
print(f'学習時:loss={loss_train:,.0f}, r2Score(決定係数)={r2score_train:.3f}') # 損失の表示
print(f'テスト時:loss={loss_test:,.0f}, r2Score(決定係数)={r2score_test:.3f}') # 損失の表示
[OUT]
==========================================================================================
Layer (type:depth-idx) Output Shape Param #
==========================================================================================
Net -- --
├─Linear: 1-1 [128] 3,456
├─ReLU: 1-2 [128] --
├─Dropout: 1-3 [128] --
├─Linear: 1-4 [64] 8,256
├─ReLU: 1-5 [64] --
├─Linear: 1-6 [1] 65
==========================================================================================
Total params: 11,777
Trainable params: 11,777
Non-trainable params: 0
Total mult-adds (M): 0.97
==========================================================================================
Input size (MB): 0.00
Forward/backward pass size (MB): 0.00
Params size (MB): 0.05
Estimated Total Size (MB): 0.05
==========================================================================================
学習時:loss=408,481, r2Score(決定係数)=0.974
テスト時:loss=409,553, r2Score(決定係数)=0.974
別添
別添1:深層学習の特徴を整理
過去の深層学習の経緯を確認しながらモデルには何が重要かを箇条書きにしました。なおソースの一部はAIciaさんのYoutubeを参考にしています。
誤差逆伝搬を使用すれば複雑なモデルでも学習可能
活性化関数にSigmoid関数を使用すると逆伝搬時に勾配消失が起こるけど、ReLUを使うと解消されるため深い層のモデルも使用可能
データはtrain/testデータに分ける必要がある
過学習の抑制にはdropoutが有効(最近はBatchNormalizationも使用):sparse(疎)なパラメータをdense(密)にする
複雑なモデルを使用する場合は大量のデータがないと過学習する
SGD(確率的勾配降下法)は”局所解”になるけど実用的には問題ない。
別添2:全結合(MLP)のハイパーパラメータ
全結合(多層パーセプトロン:MLP)のハイパラ+αは下記があります。
Layer数
Layerあたりのノード(ユニット)数
活性化関数(ReLU, Sigmoid)
損失関数
最適化関数
バッチサイズ
エポック数(訓練回数)※Early stoppingの設定有無
学習率
過学習防止(Dropout、 正則化、BatchNorm, Early stopping)
前処理(正規化、標準化)
訓練・検証用データの分割数(比率)
参考資料
資料1:技術
PYTORCH PERFORMANCE TUNING GUIDE Szymon Migacz, 04/12/2021
Googleが深層学習のノウハウを公開して話題だけど、実際読んで想像以上に価値を感じた。
— goto@meta翻訳開発者 (@goto_yuta_) January 20, 2023
例えば「バッチサイズはバリデーションセットでの性能に影響
せず、むしろバッチサイズを下げてサンプルがばらついて正則化の効果を持ったりする」みたいの詳細知識が満載だった...https://t.co/LZNiRxiOgW
資料2:図示・可視化
資料3:チュートリアル
This tutorial will introduce compute and data-efficient transformers and provide a step-by-step to create your own Vision Transformers. Through this guide, you'll be able to train state of the art results for classification in both computer vision & NLP. https://t.co/d3bc7ijeBJ
— PyTorch (@PyTorch) June 28, 2021
あとがき
次はtorchvisionを記載。ここまで来たらオートエンコーダーも作れるはずだけど、とりあえずCNNを先にしたい。
