深層学習(ディープラーニング)：逆伝搬

１．概要

ディープラーニングのパラメータ（重みやバイアスなど）を更新する手法である誤差逆伝播法(Back Propagation)を数値の流れも含めて説明します。
自分も忘れることが多いので、参考用として作成しました。

２．必要な基礎知識

学習のために必要な知識を記載します（説明は紹介程度のみ）。

微分：数式の傾きを表します。機械学習では勾配と呼びます。
連鎖律(Chain Rule)：ある微分において$${\frac{dL}{dw}=\frac{dL}{dU}\frac{dU}{dw}}$$のような形に数式変換できるルールです。
学習率(Learning rate)：重みやバイアスなどのパラメーターを勾配で更新する時に勾配にかける係数です。勾配でパラメーターを学習するため、パラメーターに勾配を渡す割合を決めるものです。
合成関数：合成関数とは関数を組み合わせた（連結させた）ものであり、入力値を連続で指定した関数で処理させるようにした関数です。詳細は過去記事をご参照ください。

３．そもそも逆伝搬は何ができるの？

複雑な合成関数から求めたい変数の微分(勾配)を簡単に求めることができます。機械学習の場合、損失関数から重みwやバイアスbの傾きを計算することができるためその勾配からパラメーターを更新することができます。
(※もし逆伝搬がないと合成関数を直接微分して微分式を求める必要があり、それは非常に大変です。)

４．損失関数

データの正解値と計算の予測値を比較するための関数です。正解値と予測値が大きく離れていると損失関数の計算値：Loss (つまりデータの精度の悪さ)は大きくなり、近いと0に近づきます。
分類問題には交差エントロピー、回帰分析(数値を予測する問題)には平均二乗誤差(正解値と予測値の差分を2乗した合計値÷データ数)などが使用されます。
目的としては損失関数から得られる誤差を最小にするために重みwを最適化することです。MSEの場合、数式は下に凸であり傾き=0の時のwが最適値となるため重みから勾配(×学習率)を引くことで更新できます。

５．逆伝搬の図解

逆伝搬を理解するためのフローを簡単に説明します。

５－１．逆伝搬1：合成関数の分解

下記のような線形モデルにおいて逆伝搬を実施してみる。

入力値：x
計算モデル(関数)M = wx + b  (w：重み、b：バイアス)
正解値：yc (関数Mから予測される数値に対する正しい値)
損失関数（2乗誤差）：(M - yc)^2 = (wx + b - yc)^2

まずは計算フローを和差積商や2乗の関数に分ける※。（ここでのポイントは分解した関数そのものが微分可能であること）
下記より損失関数は掛け算・足し算・引き算・2乗の合成関数であることがわかります。

５－２．逆伝搬2:連鎖律により勾配計算

損失関数から得られる誤差を下げるため重みwを更新するための損失関数の勾配dL/dwを求めていきます。
（※当たり前のことをたくさん書きますが自分の頭の整理用です。）
まずイメージとして各関数（掛け算・足し算・引き算・2乗）の出力値は入力値を使用しています。よってそれぞれを関数（掛け算I・足し算M・引き算D・2乗L）として考えた時にフローは下記のように記載できます。

次に損失関数の勾配を求めます。まず参考用として逆伝搬ではなく普通に求めてみます。結果は下記のとおりです。

$$
\frac{dL}{dw} = \frac{dL}{dD}\frac{dD}{dw} = \frac{dD^2}{dD}\frac{d((wx + b) - yc)}{dw} = 2D× x = 2x((wx + b) - yc)
$$

次に逆伝搬で求めてみます。連鎖律よりdL/dwは下記のとおりです。

$$
\frac{dL}{dw} = \frac{dL}{dD}\frac{dD}{dM}\frac{dM}{dI}\frac{dI}{dw}
$$

　連鎖律の式に従って各項を計算すると下記のとおりです。
※関数を通って出力された値は関数の入力値を使用している。入力値を変数で置き換えてあげれば、連鎖律ができるイメージがつかみやすい。

５－３．逆伝搬3:パラメーター(重み・バイアス)の更新

実際に数値を入れて勾配を更新してみる。

【使用した値】　入力値x：5、重みw：10、バイアスb：1、正解値yc：48

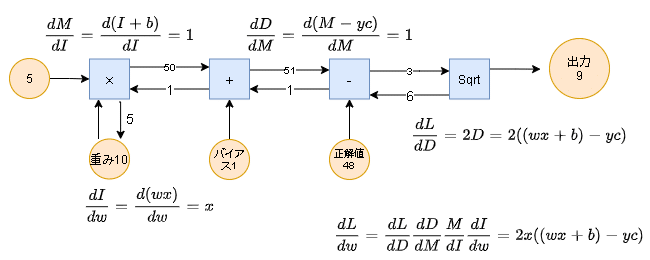
結果として勾配は6×1×1×5=30であり求めたい勾配を計算することができた（※図では各勾配を記載しているため、dL/dwを計算する場合はすべてかける必要がある。）。この勾配に適当に決めた学習率(例：0.01)をかけたものを重みwから引くことでLossを低下させることが可能である。
(※実際はdL/dbも求めてバイアスも更新します。)

６．逆伝搬のポイント

フローより下記が確認できました。

● 損失関数の微分を直接計算せずに、入力に使用した値だけ(x, w, b, yc)で求める勾配を計算できた。
● 各関数の微分は簡単な結果で出力できる。例として足し算・引き算の勾配は1であり後流側に前の勾配値をそのまま流す。掛け算だとinputとは別の変数をかけた値を後流に流す。
●どれだけ層が深くなっても計算可能である。

【参考】勾配消失

よく「深い層のディープラーニングでは勾配消失が生じるため、活性化関数でシグモイド関数を使用できない」と聞いて理解ができなかった。
上記フローで考えると下記が理由であることがすんなりわかります。

1. 連鎖律を使用すると必ず活性化関数を微分したものをかける必要がある
2. シグモイド関数の微分の最大値は0.25
3. 層が深いと0.25以下の数値を何回もかける必要がある