＜学習シリーズ＞線形モデル編：単回帰分析

１．概要

１－１．緒言

　本記事は”学習シリーズ”として自分の勉強備忘録用になります。

　過去の記事で機械学習・AIの記事を多数作成しましたが、シンプルな線形モデルは外挿が比較的得意のためいろんな分野で使用されます。
　本記事では一から線形モデルを学びなおしたいと思います。

Pythonライブラリ（機械学習・AI）｜KIYO｜note

勉強・メモ用マガジン｜KIYO｜note

チュートリアル — ディープラーニング入門：Chainer チュートリアル

　今後記載していくモデルは下記の通りです。

• 重回帰

• ロジスティック回帰

• Ridge回帰

• Rasso回帰

• ガウス過程回帰

１－２．用語・記号の説明（全般）

　本記事で使用する用語および記号は下記の通りです。

【用語一覧】

●回帰 (regression)：実数値を予測する問題
●分類 (classification)：カテゴリ（離散値）を予測する問題
●教師あり学習 (supervised learning)：機械学習でデータセットに対して正解値（ラベル）がある学習方法
●教師なし学習 (unsupervised learning)：機械学習でデータセットに対して正解値（ラベル）が無い学習方法
●予測値 (predicted value)：関数で計算された出力変数y（用語は下記参照）
●目標値 (target value)：予測値がとるべき値（教師あり学習の正解値）
●目的関数 (objective function)：機械学習において性能の良さの指標を表す関数です。一般的には”予想値と目標値の差異”から作成される関数であり、この関数を最小化することでよいモデルと判断します。
●多重共線性（multicollinearity）：多変量解析（重回帰分析など）において、いくつかの説明変数間で線形関係（強い相関関係）があると共線性といい、共線性が複数認められる場合は多重共線性があると言います。
●二乗和誤差 (sum-of-squares error)：正解値$${y}$$と予測値$${\hat{y}}$$の差の２乗$${(y-\hat{y})^2}$$です。これをモデルと正解値の誤差とも呼びます。
●最小二乗法：二乗和誤差を最小化することでモデルの当てはまりを最適化する手法です。

【記号一覧】

●$${f()}$$：$${y=f(x)}$$におけるf()であり関数と呼びます。中身は入力変数xを処理して新しい出力変数yを生成する計算式です。
●$${x}$$：$${y=f(x)}$$におけるxです。複数は下記の通り複数あります。
　名称１：説明変数（Explanatory variable）
　名称２：独立変数（Independent variable）
　名称３：外生変数（Exogenous variable）
　名称４：入力変数（Input variable）
　名称５：入力値（Input value）
●$${y}$$：$${y=f(x)}$$におけるyです。複数は下記の通り複数あります。
　名称１：目的変数（Response variable）
　名称２：従属変数（Dependent variable）
　名称３：被説明変数（Explained variable）
　名称４：内生変数（endogenous variable）
　名称５：出力変数（Output variable）
　名称６：予測値/推論値（prediction value）
●$${w_i}$$(weight)：重み（単回帰の場合は傾きとも言う）
●$${b}$$(bias)：バイアス（単回帰の場合は切片とも言う）

１－３．サンプル用データ

　サンプルデータはScikit-learnのToy datasetsを使用します。今回は回帰(Regression)のため"diabetes"を使用しました。単回帰は変数が1つだけの1次元モデルのため、特徴量として重要な"s5"だけ抽出しました。

[IN]
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

#データセットの読み込み
diabetes = datasets.load_diabetes()
data, target = diabetes.data, diabetes.target
df_data = pd.DataFrame(data, columns=diabetes.feature_names)
df_data = df_data[['s5']] #単回帰として使用するため1次元のみ抽出
print(type(df_data), df_data.shape, type(target), target.shape)

#データの可視化
fig, ax = plt.subplots(1, 1, figsize=(10, 5), facecolor='w')
ax.scatter(df_data, target)
ax.set(xlabel='s5', ylabel='target', title='Correlation of Diabetes')
plt.grid()
plt.show()

[OUT]
<class 'pandas.core.frame.DataFrame'> (442, 1) <class 'numpy.ndarray'> (442,)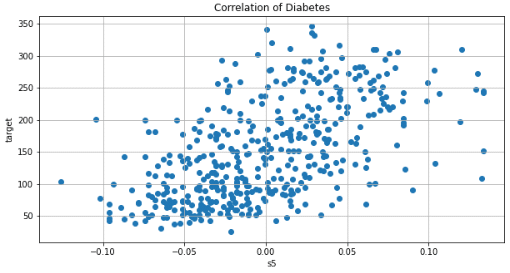

7.1. Toy datasets

２．単回帰（線形モデル）とは：y=ax+b

　単回帰分析とは 1 つの入力変数$${x}$$から 1 つの出力変数$${y}$$を推測する処理です。入力値に重みをかけバイアスを足したものを回帰方程式、グラフを回帰直線と呼びます。モデルの形が直線になることから線形モデルとも呼ばれます。

$$
単回帰：y = ax+b
$$

●$${x}$$：入力変数
●$${y}$$(または$${\hat y}$$)：出力変数
●$${a}$$：傾き(機械学習では重みと呼び$${w}$$を使う）
●$${b}$$：切片（またはバイアス）

　推定値$${\hat y}$$とデータ値$${y_i}$$の誤差を最小にすることで最適なパラメータ$${a}$$, $${b}$$を決定できます。

３．直接解法の計算

　深層学習（ディープラーニング）などではモデルの学習時に誤差逆伝搬を使用して学習させますが、単回帰の重みとバイアスは直接計算可能です。
　最小二乗法を用いて誤差が最小になるパラメータを直接計算してみます。

３－１．結論

　求めたいパラメータ(傾き$${a}$$, 切片$${b}$$)は下記で計算できます。

$$
a =\frac{\frac{1}{n}\sum_{i=1}^{n} x_iy_i - \bar{y}\bar{x}}{\frac{1}{n}\sum_{i=1}^{n} x_i^2 - \bar{x}^2}=\frac{Cov(X,Y)}{Var(X)}
$$

$$
b=\bar{y}-a\bar{x}
$$

　参考までに展開した状態だと下記の通りです。

$$
\begin{aligned}
a &= \frac{n \sum_{i=1}^{n} x_iy_i - \sum_{i=1}^{n} x_i \sum_{i=1}^{n} y_i}{n \sum_{i=1}^{n} x_i^2 - (\sum_{i=1}^{n} x_i)^2}
\\ b &= \frac{ (\sum_{i=1}^{n} x_i^2)\sum_{i=1}^{n} y_i - (\sum_{i=1}^{n} x_i)\sum_{i=1}^{n} x_iy_i }{n \sum_{i=1}^{n} x_i^2 - (\sum_{i=1}^{n} x_i)^2}
\end{aligned}
$$

３－２．用語・数式の一覧

　まずは各種変数を用語・数式を示します。統計の用語は下記に詳細を記述しております。

$$
入力変数x = \begin{pmatrix}x_1 \ x_2 \ \cdots \ x_n\end{pmatrix} 
$$

$$
出力変数y = \begin{pmatrix}y_1 \ y_2 \ \cdots \ y_n\end{pmatrix}
$$

　３－２－１．平均値

　平均値とは「全データを合計値をデータ数Nで割ったもの」でありデータの重心を意味します。下記より、$${n\bar{x}=\sum_{i=1}^{n} x_i }$$(要素数×平均値=各要素の合計値)への変換が可能です。

$$
xの平均値：\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i = \frac{1}{n} \begin{pmatrix} x_1 + x_2 + \cdots + x_n \end{pmatrix}
$$

$$
yの平均値：\bar{y} = \frac{1}{n} \sum_{i=1}^{n} y_i = \frac{1}{n} \begin{pmatrix} y_1 + y_2 + \cdots + y_n \end{pmatrix}
$$

　３－２－２．分散

　分散とは「平均値から各データの差の2乗を全て足した値」でありデータのばらつきを表します（下記式は標本分散となります）。

$$
xの分散\sigma_x^2 = \frac{1}{n}\sum_{i=1}^{n} (x_i - \bar{x})^2=\frac{1}{n}\sum_{i=1}^{n} x_i^2 - \bar{x}^2
$$

　右辺の式導出は下記の通りです。

$$
\sigma_x^2 の式展開= \frac{1}{n}\sum_{i=1}^{n} (x_i - \bar{x})^2= \frac{1}{n}\sum_{i=1}^{n} (x_i^2 - 2x_i \bar{x} + \bar{x}^2)
$$

$$
= \frac{1}{n}(\sum_{i=1}^{n} x_i^2 - 2\bar{x}\sum_{i=1}^{n} x_i + \sum_{i=1}^{n} \bar{x}^2)
$$

$$
= \frac{1}{n}(\sum_{i=1}^{n} x_i^2 - 2n\bar{x}^2 + n \bar{x}^2)=\frac{1}{n}\sum_{i=1}^{n} x_i^2 - \bar{x}^2
$$

　３－２－３．共分散

　共分散とは「二組の対応するデータの間の関係を表す数値」であり、X の偏差 × Y の偏差の平均=(x-平均のx)(y-平均のy)の平均で計算できます。

$$
共分散行列Cov(x,y) = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})= \frac{1}{n}\sum_{i=1}^{n} x_iy_i - \bar{x}\bar{y}
$$

$$
Covの展開=\frac{1}{n} \begin{pmatrix} (x_1-\bar{x})(y_1-\bar{y}) + (x_2-\bar{x})(y_2-\bar{y}) + \cdots + (x_n-\bar{x})(y_n-\bar{y}) \end{pmatrix}
$$

$$
右辺式の導出：\frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})= \frac{1}{n} \sum_{i=1}^{n} (x_iy_i - x_i \bar{y} - \bar{x}y_i + \bar{x}\bar{y})
$$

$$
= \frac{1}{n}(\sum_{i=1}^{n} x_iy_i - \bar{y}\sum_{i=1}^{n} x_i - \bar{x}\sum_{i=1}^{n} y_i + n\bar{x}\bar{y})=\frac{1}{n}(\sum_{i=1}^{n} x_iy_i - \bar{y}(n\bar{x})- \bar{x}(n\bar{y}) + n\bar{x}\bar{y})
$$

$$
= \frac{1}{n}(\sum_{i=1}^{n} x_iy_i - n\bar{x}\bar{y})=\frac{1}{n}\sum_{i=1}^{n} x_iy_i - \bar{x}\bar{y}
$$

３－３．重みとバイアスの導出

　３－３－１：最小二乗和Eの計算

　まずは最小化したい二乗和誤差を計算します。

$$
二乗和誤差E=\sum_{i=1}^{n}(y_i-\hat{y})=\sum_{i=1}^{n} (y_i - (ax_i + b))^2
$$

　求めたい傾きaと切片bを求めるには、aとbそれぞれで二乗和誤差Eが最小になる値、つまりEに対する偏微分が0になる値$${\frac{\partial E}{\partial a}=0}$$, $${\frac{\partial E}{\partial b}=0}$$を求めます。

$${(y_i - (ax_i + b))^2 }$$を分解してaとbそれぞれでまとめると下記の通りです。

$$
E=(y_i - (ax_i + b))^2= y_i^2 - 2y_i(ax_i + b) + (ax_i + b)^2
$$

$$
=y_i^2 - 2y_i(ax_i + b) + a^2 x_i^2 + 2abx_i + b^2
$$

　３－３－２．aでの偏微分を計算

　二乗和誤差Eをaでまとめると下記の通りです。

$$
E= \sum_{i=1}^{n} (x_i^2a^2+(2bx_i-2x_iy_i)a+ (b^2 - 2by_i + y_i^2))
$$

　上記をaで偏微分すると下記の通りです。

$$
\begin{aligned}
\frac{\partial E}{\partial a} = \sum_{i=1}^{n} (2a x_i^2 + 2(bx_i - x_iy_i)) \\
=2a \sum_{i=1}^{n} x_i^2 + 2 \sum_{i=1}^{n} (bx_i - x_iy_i) \\
=2a \sum_{i=1}^{n} x_i^2 +2b\sum_{i=1}^{n}x_i-2\sum_{i=1}^{n} x_iy_i
\end{aligned}
$$

　$${\frac{\partial E}{\partial a}=0}$$より、aで整理すると下記の通りです。

$$
a = \frac{\sum_{i=1}^{n} x_iy_i - b\sum_{i=1}^{n} x_i}{\sum_{i=1}^{n} x_i^2}
$$

　$${y=ax+b}$$より上式に$${b=y-ax}$$を代入するとbが消せます。

$$
a = \frac{\sum_{i=1}^{n} x_iy_i - (\bar{y} - a\bar{x})\sum_{i=1}^{n} x_i}{\sum_{i=1}^{n} x_i^2}
$$

$$
a\sum_{i=1}^{n} x_i^2 = \sum_{i=1}^{n} x_iy_i - \bar{y}\sum_{i=1}^{n} x_i + a\bar{x}\sum_{i=1}^{n} x_i
$$

$$
a\left(\sum_{i=1}^{n} x_i^2\right) = \sum_{i=1}^{n} x_iy_i - \bar{y}\left(\sum_{i=1}^{n} x_i\right) + a\bar{x}\left(\sum_{i=1}^{n} x_i\right)
$$

　aで整理すると

$$
a = \frac{\sum_{i=1}^{n} x_iy_i - \bar{y}\sum_{i=1}^{n} x_i}{\sum_{i=1}^{n} x_i^2 - \bar{x}\sum_{i=1}^{n} x_i}
$$

$$
a = \frac{\sum_{i=1}^{n} x_iy_i - \bar{y}n\bar{x}}{\sum_{i=1}^{n} x_i^2 - n\bar{x}^2}
$$

$$
a = \frac{\frac{1}{n}\sum_{i=1}^{n} x_iy_i - \bar{y}\bar{x}}{\frac{1}{n}\sum_{i=1}^{n} x_i^2 - \bar{x}^2}=\frac{Cov(X,Y)}{Var(X)}
$$

　３－３－３．bでの偏微分を計算

　二乗和誤差Eをbでまとめると下記の通りです。

$$
E= \sum_{i=1}^{n}(b^2+(-2y_i2ax_i)b + (y_i^2 - 2ax_i y_i+ a^2 x_i^2 ))
$$

　上記をbで偏微分すると下記の通りです。

$$
\begin{aligned}
\frac{\partial E}{\partial b} = \sum_{i=1}^{n} (2b - 2y_i + 2ax_i) \\
= 2 \sum_{i=1}^{n} b - 2 \sum_{i=1}^{n} y_i + 2a \sum_{i=1}^{n} x_i
\end{aligned}
$$

$$
=2nb- 2 \sum_{i=1}^{n} y_i + 2a \sum_{i=1}^{n} x_i
$$

　$${\frac{\partial E}{\partial b}=0}$$のためbで整理すると、

$$
b =\frac{1}{n} \sum_{i=1}^{n} y_i - \frac{1}{n}a \sum_{i=1}^{n} x_i=\bar{y}-a\bar{x}
$$

３－４．コラム：重みとバイアスの導出（行列編）

　参考として上記の正規方程式を行列でも解いてみます。

$$
\begin{aligned}\frac{\partial E}{\partial a} = \sum_{i=1}^{n} (2a x_i^2 + 2(bx_i - x_iy_i)) \\=2a \sum_{i=1}^{n} x_i^2 +2b\sum_{i=1}^{n}x_i-2\sum_{i=1}^{n} x_iy_i
\\=2(a \sum_{i=1}^{n} x_i^2 +b\sum_{i=1}^{n}x_i-\sum_{i=1}^{n} x_iy_i)
\end{aligned}
$$

$$
\begin{aligned}\frac{\partial E}{\partial b} = \sum_{i=1}^{n} (2b - 2y_i + 2ax_i) \\= 2 \sum_{i=1}^{n} b - 2 \sum_{i=1}^{n} y_i + 2a \sum_{i=1}^{n} x_i
\\= 2(\sum_{i=1}^{n} b - \sum_{i=1}^{n} y_i + a \sum_{i=1}^{n} x_i)
\end{aligned}
$$

$${\frac{\partial E}{\partial a}=0}$$, $${\frac{\partial E}{\partial b}=0}$$より

$$
a \sum_{i=1}^{n} x_i^2 +b\sum_{i=1}^{n}x_i=\sum_{i=1}^{n} x_iy_i
$$

$$
a \sum_{i=1}^{n} x_i + \sum_{i=1}^{n} b =\sum_{i=1}^{n} y_i
$$

　これを行列で記載すると単回帰の正規方程式の行列が得られます。

$$
\begin{bmatrix} \sum_{i=1}^{n} x_i^2 & \sum_{i=1}^{n} x_i \\ \sum_{i=1}^{n} x_i & n \end{bmatrix} \begin{bmatrix} a \\ b \end{bmatrix} = \begin{bmatrix} \sum_{i=1}^{n} x_iy_i \\ \sum_{i=1}^{n} y_i \end{bmatrix}
$$

　両辺に左辺にある逆行列をかけるとパラメータが得られます。

$$
\begin{bmatrix} a \\ b \end{bmatrix} = \frac{1}{\left(n \sum_{i=1}^{n} x_i^2 - (\sum_{i=1}^{n} x_i)^2\right)} \begin{bmatrix} n & -\sum_{i=1}^{n} x_i \\ -\sum_{i=1}^{n} x_i & \sum_{i=1}^{n} x_i^2 \end{bmatrix} \begin{bmatrix} \sum_{i=1}^{n} x_iy_i \\ \sum_{i=1}^{n} y_i \end{bmatrix}
$$

　上記計算より、連立方程式で求めた解と同じになることが確認できます。

$$
\begin{bmatrix} a \\b \end{bmatrix}=
\frac{1}{\left(n \sum_{i=1}^{n} x_i^2 - (\sum_{i=1}^{n} x_i)^2\right)}
\begin{bmatrix}
n\sum_{i=1}^{n} x_iy_i - \sum_{i=1}^{n} x_i \sum_{i=1}^{n} y_i \\
\sum_{i=1}^{n} x_i^2 \sum_{i=1}^{n} y_i-\sum_{i=1}^{n} x_i \sum_{i=1}^{n} x_iy_i
\end{bmatrix}
$$

【参考：逆行列の計算】

$$
\begin{bmatrix} A & B \\ C & D \end{bmatrix}^{-1} = \frac{1}{AD - BC} \begin{bmatrix} D & -B \\ -C & A \end{bmatrix}
$$

４．単回帰モデルの実装：スクラッチ編

　動作を理解するためにPythonのライブラリを使用せずスクラッチで計算します。目視で確認できるようにデータ数を1桁に調整しました。

[IN]
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
import os

from sklearn import datasets
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split

#データセットの読み込み
diabetes = datasets.load_diabetes()
data, target = diabetes.data, diabetes.target
df_data = pd.DataFrame(data, columns=diabetes.feature_names)
df_data = df_data[['s5']] #単回帰として使用するため1次元のみ抽出

#データの分割：参照用のデータ数を少なくする
x_train, x_test, y_train, y_test = train_test_split(df_data, target, test_size=0.98, random_state=0)
print(f'x_train: {x_train.shape}, x_test: {x_test.shape}, y_train: {y_train.shape}, y_test: {y_test.shape}')

#Excel処理用としてデータを結合／出力
array_dataset = np.concatenate([x_train, y_train.reshape(-1, 1)], axis=1)
df_dataset = pd.DataFrame(array_dataset, columns=['x', 'y'])
display(df_dataset)

#Excelファイルの出力
if not os.path.exists('data'):
    os.mkdir('data') #ディレクトリが存在しない場合のみ作成
    print(f'ディレクトリを作成しました: {os.path.abspath("data")}')

df_dataset.to_excel('data/dataset_diabetes.xlsx', index=False)

#データの可視化
fig, ax = plt.subplots(1, 1, figsize=(10, 5), facecolor='w')
ax.scatter(x_train, y_train)
ax.set(xlabel='s5', ylabel='target', title='Correlation of Diabetes')
plt.grid()
plt.show()

[OUT]
x_train: (8, 1), x_test: (434, 1), y_train: (8,), y_test: (434,)

　　x　　　　	y
0	0.014823	311.0
1	0.007837	122.0
2	0.084495	243.0
3	0.129019	248.0
4	-0.029528	91.0
5	0.079121	281.0
6	-0.018118	142.0
7	0.073410	295.0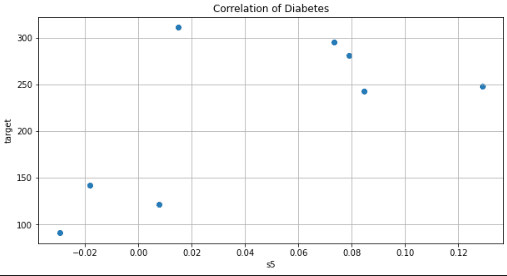

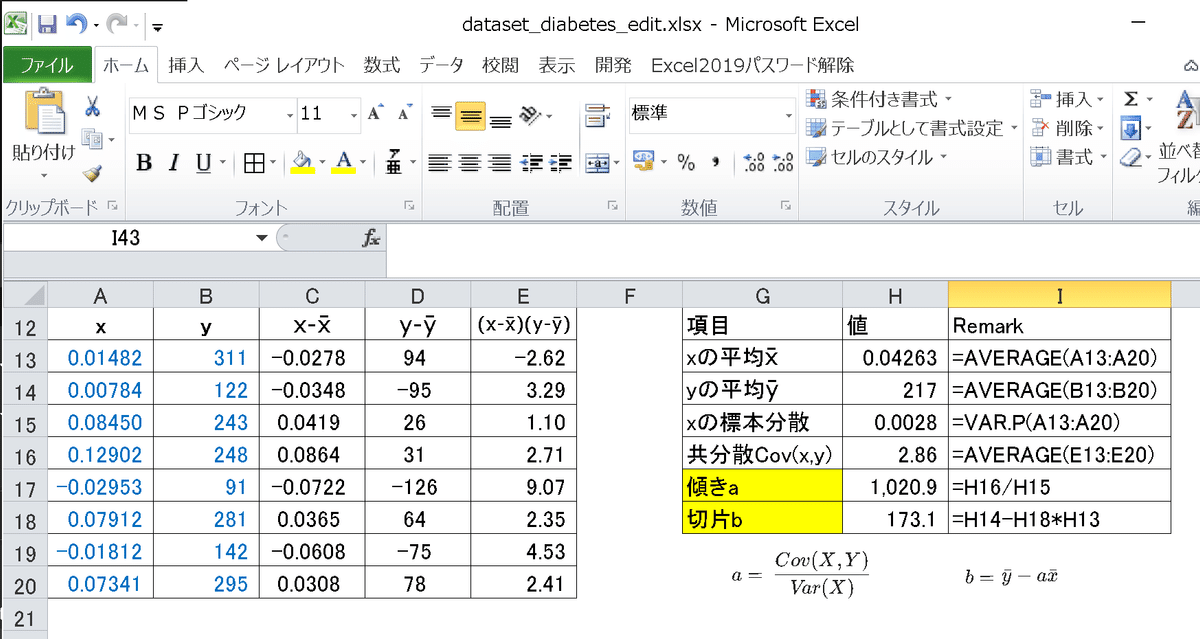
４－１．Excelで計算

　単回帰はExcelでも手動で簡単に計算できます。計算式は前述の通りです。傾き(重み)は2パターンで計算してみました。

$$
a =\frac{\frac{1}{n}\sum_{i=1}^{n} x_iy_i - \bar{y}\bar{x}}{\frac{1}{n}\sum_{i=1}^{n} x_i^2 - \bar{x}^2}=\frac{Cov(X,Y)}{Var(X)}
$$

$$
b=\bar{y}-a\bar{x}
$$

４－２．Pythonで計算

　Pythonで行列・ベクトルなどの計算をする場合はNumpyやPandasが便利であるためこれらを使用して計算します。
　NumpyとPandasで計算する場合の注意点は下記の通りです。

1. 分散はデフォルトだとNumpyは標本分散、Pandasは不偏分散で出力

2. np.cov()はddof=0で標本分散、ddof=1で不偏分散で出力(default:ddof=1)

[IN]
xarray_train = x_train.values #DataFrameをNumpy配列に変換
print(f'x_train:{xarray_train.shape}, y_train:{y_train.shape}, xarray_train:{type(xarray_train)}, y_train:{type(y_train)}')

#統計量を計算
x_mean = xarray_train.mean() #xの平均値
y_mean = y_train.mean() #yの平均値
x_var = xarray_train.var() #xの標本分散※Numpyのvar()は不偏分散

#共分散を計算
datasets = np.concatenate([xarray_train, y_train.reshape(-1, 1)], axis=1) #列方向に結合してデータセット作成
Cov = np.cov(xarray_train.T, y_train, ddof=0) #ddof=0で標本分散, ddof=1で不偏分散
Cov_xy = Cov[0, 1] #xとyの共分散

slope = Cov_xy / x_var #傾き
intercept = y_mean - slope * x_mean #切片
print(f'xの平均値: {x_mean:.5f}, yの平均値: {y_mean}, xの標本分散: {x_var:.5f}, 共分散: {Cov_xy:.5f}')
print(f'傾き: {slope:.2f}, 切片: {intercept:.3f}')

[OUT]
x_train:(8, 1), y_train:(8,), xarray_train:<class 'numpy.ndarray'>, y_train:<class 'numpy.ndarray'>

xの平均値: 0.04263, yの平均値: 216.625, xの標本分散: 0.00280, 共分散: 2.85528
傾き: 1020.85, 切片: 173.104

【補足：np.cov()における共分散行列の出力確認】
　np.cov()で共分散行列を出力できます。出力は下記の通りであり,
XYの共分散は$${cov_{xy}}$$や$${cov_{yx}}$$から抽出できます。

$$
\Sigma
=\begin{bmatrix} cov_{xx} & cov_{xy} \\ cov_{yx} & cov_{yy} \end{bmatrix}
=\begin{bmatrix} xの分散 & XYの共分散 \\ YXの共分散 & yの分散 \end{bmatrix}
=\begin{bmatrix} s^{2}_{xx} & cov_{xy} \\ cov_{yx} & s^{2}_{yy} \end{bmatrix} 
$$

　注意点としてnp.cov()には引数"ddof"があり、この値で標本分散と不偏分散を選択できますがデフォルト値:ddof=1(不偏分散)のため、今回は"ddof=0"を指定しました。
　出力の形式及び結果は下記の通りです。

[IN]
xarray_train = x_train.values #DataFrameをNumpy配列に変換
print(f'x_train:{xarray_train.shape}, y_train:{y_train.shape}, xarray_train:{type(xarray_train)}, y_train:{type(y_train)}')

#統計量を計算
x_mean = xarray_train.mean() #xの平均値
y_mean = y_train.mean() #yの平均値
x_var = xarray_train.var() #xの標本分散※Numpyのvar()は不偏分散

#共分散を計算
Cov = np.cov(xarray_train.T, y_train, ddof=0) #ddof=0で標本分散, ddof=1で不偏分散
Cov_xy = Cov[0, 1] #xとyの共分散

slope = Cov_xy / x_var #傾き
intercept = y_mean - slope * x_mean #切片
print(f'xの平均値: {x_mean:.5f}, yの平均値: {y_mean}, xの標本分散: {x_var:.5f}, 共分散: {Cov_xy:.5f}')
print(f'傾き: {slope:.2f}, 切片: {intercept:.3f}')


#数値の確認
print(f'共分散行列(標本分散)\n {Cov}') #ddof=0
print(f'共分散行列(不偏分散)\n {np.cov(xarray_train.T, y_train)}') #ddof=1

#Seabornでヒートマップで共分散行列を可視化
plt.figure(figsize=(6, 6), facecolor='w')
plt.rcParams['font.size'] = 16
#表示：値、x軸ラベル、y軸ラベル、非表示：カラーバー
sns.heatmap(Cov, annot=True, cmap='autumn_r',
            xticklabels=['x', 'y'], 
            yticklabels=['x', 'y'], 
            cbar=False,
            fmt='.4f')

#数値の上に文字を追加
plt.text(0.5, 0.4, '$Var(x):Cov_{xx}$', ha='center', va='center', color='black', fontsize=20)
plt.text(0.5, 1.4, '$Cov_{xy}$', ha='center', va='center', color='black', fontsize=20)
plt.text(1.5, 0.4, '$Cov_{yx}$', ha='center', va='center', color='black', fontsize=20)
plt.text(1.5, 1.4, '$Var(y):Cov_{yy}$', ha='center', va='center', color='black', fontsize=20)

[OUT]
共分散行列(標本分散)
 [[   0.003    2.855]
 [   2.855 6397.234]]

共分散行列(不偏分散)
 [[   0.003    3.263]
 [   3.263 7311.125]]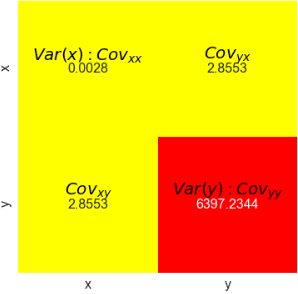

機械学習で用いる行列の単語を整理した② (分散共分散行列、相関行列) - Qiita

５．単回帰モデルの実装：ライブラリ編

　より簡単にモデルを作成するためにライブラリを使用します。

５－１．Scikit-learn：LinearRegression

　Scikit-learnを使用して単回帰を実装します。Scikit-learnのAPIはシンプルであり、ほとんどのモデルは下記で実装できます。

1. 使用する機械学習モデルをインポート

2. モデルのインスタンス化

3. 学習：model.fit()

4. 学習後のパイパーパラメータ確認

5. 推論：model.predict()

[IN]
from sklearn.linear_model import LinearRegression

#単回帰モデルの実装
linear = LinearRegression() #インスタンス化
linear.fit(x_train, y_train) #学習
print(f'傾き: {linear.coef_[0]:.2f}, 切片: {linear.intercept_:.3f}') #傾き、切片の表示
y_pred = linear.predict(x_test) #予測

[OUT]
傾き: 1020.85, 切片: 173.104

　出力も確認しました。

[IN]
#データの可視化
fig, ax = plt.subplots(1, 1, figsize=(10, 5), facecolor='w')
ax.scatter(x_train, y_train, label='データ')
ax.plot(x_test, y_pred, color='red', lw=1.0, label='回帰直線')
ax.set(xlabel='s5', ylabel='target', title='Correlation of Diabetes')
ax.text(-0.05, 200, f'y = {linear.coef_[0]:.2f}x + {linear.intercept_:.3f}', ha='center', va='center', color='red', fontsize=14)
plt.grid(), plt.legend()
plt.show()

[OUT]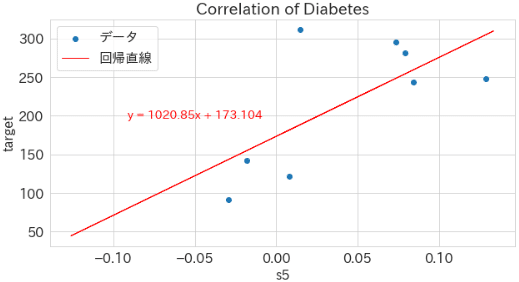

５－２．Pytorch：nn.Linear()

　Pytorchで単回帰を実装します。実装フローは下記の通りです。

1. （線形）モデルをインスタンス化

2. 各値を標準化(平均0, 分散1)※これが無いと収束しない可能性がある

3. 各種パラメータ作成(評価関数、最適化関数、学習率など)

4. 学習モードに切り替える

5. 推論値を計算(今回はバッチ学習)

6. 損失関数を使用して"正解値"と"推論値"から誤差を求める

7. loss.backward()で各パラメータの勾配を求める

8. optimizer.step()(または手動）によりパラメータを更新する

9. zero_grad()によりパラメータの勾配を初期化する

10. 5~9をループ計算する

[IN]
import torch
import torch.nn as nn
import torch.optim as optim

#データセットの読み込み
diabetes = datasets.load_diabetes()
data, target = diabetes.data, diabetes.target
df_data = pd.DataFrame(data, columns=diabetes.feature_names)
df_data = df_data[['s5']] #単回帰として使用するため1次元のみ抽出

#データの分割：参照用のデータ数を少なくする
x_train, x_test, y_train, y_test = train_test_split(df_data, target, test_size=0.98, random_state=0)

#単回帰モデルの実装
linear = nn.Linear(1, 1) #インスタンス化

#パラメータの設定
lr = 0.05 #学習率
iteration = 1000 #学習回数

criterion = nn.MSELoss() #損失関数の定義
optimizer = optim.SGD(linear.parameters(), lr=lr) #最適化手法の定義

#x_train:dataFrame, y_train:Numpyのため形が異なる
x_train_tensor, y_train_tensor = torch.tensor(x_train.values, dtype=torch.float32), torch.tensor(y_train, dtype=torch.float32) #Numpy配列をTensorに変換
print(f'x_train_tensor:{x_train_tensor.shape}, y_train_tensor:{y_train_tensor.shape}, x_train_tensor:{type(x_train_tensor)}, y_train_tensor:{type(y_train_tensor)}')


#標準化
x_mean = x_train_tensor.mean()
y_mean = y_train_tensor.mean()
x_std = x_train_tensor.std()
y_std = y_train_tensor.std()
print(f'x_mean:{x_mean:.3f}, y_mean:{y_mean:.3f}, x_std:{x_std:.3f}, y_std:{y_std:.3f}')
x_scale = (x_train_tensor- x_mean) / x_std
y_scale = (y_train_tensor - y_mean) / y_std
print(f'x_scale:{x_scale.shape}, y_scale:{y_scale.shape}, xの平均:{x_scale.mean():.1f}, yの平均:{y_scale.mean():.1f}, xの標準偏差:{x_scale.std()}, yの標準偏差:{y_scale.std()}')

#パラメータの表示
for name, param in linear.named_parameters():
    print(f'学習前|パラメータ名: {name}, 値: {param.detach().numpy()}')

#学習
linear.train() #学習モードに設定

print('=' * 50)
for iter in range(iteration):
    optimizer.zero_grad() #勾配の初期化
    output = linear(x_scale) #予測)
    loss = criterion(output, y_scale.unsqueeze(1)) #損失の計算
    loss.backward() #勾配の計算
    optimizer.step() #パラメータの更新

    if (iter + 1) % 100 == 0:
        print(f'iter: {iter + 1}, loss: {loss.item():.4f}')

print('=' * 50)


#パラメータの表示
for name, param in linear.named_parameters():
    print(f'学習後|パラメータ名: {name}, 値: {param.detach().numpy()}')
    

#標準化したモデルのパラメータを元に戻す
params_linaer = {'weight': linear.weight, 'bias': linear.bias}
weight_scale, bias_scale = params_linaer['weight'], params_linaer['bias']
weight_pytorch = weight_scale * y_std / x_std #標準化を戻す
bias_pytorch = bias_scale * y_std + y_mean - weight_pytorch * x_mean #標準化を戻す
weight_pytorch, bias_pytorch = weight_pytorch.detach().numpy(), bias_pytorch.detach().numpy()
print(f'weight_pytorch:{weight_pytorch}, bias_pytorch:{bias_pytorch}')

[OUT]
x_train_tensor:torch.Size([8, 1]), y_train_tensor:torch.Size([8]), x_train_tensor:<class 'torch.Tensor'>, y_train_tensor:<class 'torch.Tensor'>
x_mean:0.043, y_mean:216.625, x_std:0.057, y_std:85.505
x_scale:torch.Size([8, 1]), y_scale:torch.Size([8]), xの平均:-0.0, yの平均:0.0, xの標準偏差:1.0, yの標準偏差:1.0

学習前|パラメータ名: weight, 値: [[0.91]]
学習前|パラメータ名: bias, 値: [-0.466]

==================================================
iter: 100, loss: 0.4763
iter: 200, loss: 0.4763
iter: 300, loss: 0.4763
iter: 400, loss: 0.4763
iter: 500, loss: 0.4763
iter: 600, loss: 0.4763
iter: 700, loss: 0.4763
iter: 800, loss: 0.4763
iter: 900, loss: 0.4763
iter: 1000, loss: 0.4763
==================================================

学習後|パラメータ名: weight, 値: [[0.675]]
学習後|パラメータ名: bias, 値: [0.]

weight_pytorch:[[1020.852]], bias_pytorch:[[173.104]]

　最後に可視化しました。可視化時は標準化の値を元の値に変換しました。

[IN]
#推論
linear.eval() #推論モードに設定
_y_pred = linear(x_scale) #予測
y_pred = _y_pred * y_std + y_mean #標準化を戻す

#データの可視化
fig, ax = plt.subplots(1, 1, figsize=(10, 5), facecolor='w')
ax.scatter(x_train, y_train, label='データ')
ax.plot(x_train, y_pred.detach().numpy(), color='red', lw=1.0, label='回帰直線')
ax.set(xlabel='s5', ylabel='target', title='Correlation of Diabetes')
ax.text(0.06, 150, f'y = {float(weight_pytorch):.2f}x + {float(bias_pytorch):.3f}', ha='center', va='center', color='red', fontsize=14)
plt.grid(), plt.legend()
plt.show()

[OUT]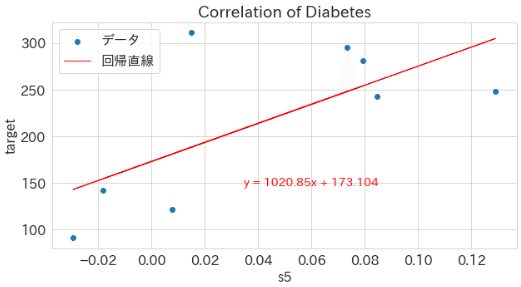

---

---

６．補足編：最尤推定による単回帰計算

　単回帰の最適パラメータ推定、つまり誤差最小化ために最小二乗法を使用しました。最小二乗法とは別に確率論を用いた最尤推定でも計算可能です。
　一般的には最小二乗法の理解だけで充分のため補足の章として説明します。なお、最尤推定を理解したい方は別記事に記載しております。

６－１．サンプルデータ準備

　データは４章で使用したDiabetesデータセットを使用し、目視で確認できるようにデータ数を1桁に調整しました。

[IN]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib
import os

from sklearn import datasets
from sklearn.model_selection import train_test_split

#データセットの読み込み
diabetes = datasets.load_diabetes()
data, target = diabetes.data, diabetes.target
df_data = pd.DataFrame(data, columns=diabetes.feature_names)
df_data = df_data[['s5']] #単回帰として使用するため1次元のみ抽出

#データの分割：参照用のデータ数を少なくする
x_train, x_test, y_train, y_test = train_test_split(df_data, target, test_size=0.98, random_state=0)
print(f'x_train: {x_train.shape}, x_test: {x_test.shape}, y_train: {y_train.shape}, y_test: {y_test.shape}')
print(f'x_train: {type(x_train)}, x_test: {type(x_test)}, y_train: {type(y_train)}, y_test: {type(y_test)}')

#出力用としてデータを結合／出力
array_dataset = np.concatenate([x_train, y_train.reshape(-1, 1)], axis=1)
df_dataset = pd.DataFrame(array_dataset, columns=['x', 'y'])
display(df_dataset)

#データの可視化
fig, ax = plt.subplots(1, 1, figsize=(8, 5), facecolor='w')
ax.scatter(x_train, y_train)
ax.set(xlabel='s5', ylabel='target', title='Correlation of Diabetes')
plt.grid()
plt.show()

[OUT]
x_train: (8, 1), x_test: (434, 1), y_train: (8,), y_test: (434,)
x_train: <class 'pandas.core.frame.DataFrame'>, x_test: <class 'pandas.core.frame.DataFrame'>, y_train: <class 'numpy.ndarray'>, y_test: <class 'numpy.ndarray'>


	x	　　　　　y
0	0.014823	311.0
1	0.007837	122.0
2	0.084495	243.0
3	0.129019	248.0
4	-0.029528	91.0
5	0.079121	281.0
6	-0.018118	142.0
7	0.073410	295.0

６－２．正規分布と尤度

　確率モデルを扱う上で理解が必須である正規分布と尤度について簡単に説明します。詳細は別記事参照のこと。

　６－２－１．正規分布

　正規分布とは連続値を扱う確率密度分布の一つであり自然現象などにおけるばらつきを表現できます。平均値$${\mu}$$, 分散$${\sigma^2}$$を用いて下記数式で表現でき、$${\mu=0}$$, 分散$${\sigma^2=1}$$の場合を標準正規分布と呼びます。

$$
\mathcal{N}(\mu, \sigma^2)=f(x)=\dfrac{1}{\sqrt{2\pi\sigma^2}}\exp(-\dfrac{(x-\mu)^ 2}{2\sigma^ 2})
$$

[IN]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib
import os
from scipy import stats

def plot_line(x, y, ax, label, x_label, y_label, title):
    ax.plot(x, y, label=label)
    ax.set(xlabel=x_label, ylabel=y_label, title=title)
    ax.grid(), ax.legend()
    plt.show()

def normal_distribution(x, mu, sigma):
    return 1 / (np.sqrt(2 * np.pi) * sigma) * np.exp(-(x - mu) ** 2 / (2 * sigma ** 2)) # 正規分布

x = np.linspace(-5, 5, 1000)
y = normal_distribution(x, 0, 1) # 平均0, 標準偏差1の正規分布(標準正規分布)

fig, ax = plt.subplots(figsize=(10, 6), facecolor="w")
plot_line(x, y, ax, "標準正規分布", "x", "y", "標準正規分布")

[OUT]

　６－２－２．尤度

　尤度とはデータに対するパラメータの尤もらしさを表します。正規分布はパラメータとして平均値$${\mu}$$, 分散$${\sigma^2}$$を持っていますがデータ$${x}$$に対して尤もらしいパラメータを表現します。

$$
\mathcal{N}(\mu, \sigma^2)=f(x)=\dfrac{1}{\sqrt{2\pi \sigma^2}} \exp \left(-\frac{(x - \mu)^2} {2\sigma^2} \right) \hspace{20px} (-\infty < x < \infty)
$$

　例としてデータ[10, 14, 20, 22]があり正規分布のパラメータ$${\mu}$$, $${\sigma^2}$$を変化させたとき尤もらしいパラメータが存在します。
　下図の例では右下の図、つまり正規分布の中心にデータが集まっており確率的にデータの出現数が多い場所が尤もらしいと判断できます。

[IN]
def plot_line(x, y, ax, label, x_label, y_label, title, varbose=True):
    if varbose:
        ax.plot(x, y, label=label)
    else:
        ax.scatter(x, y, label=label, color="r", edgecolors="k")
        ax.set(xlabel=x_label, ylabel=y_label, title=title)
        ax.grid(), ax.legend()

def calc_likelihood(data, mu, sigma):
    likelihoods = stats.norm.pdf(data, mu, sigma)
    likelihood = np.prod(likelihoods)
    return likelihood
    
    
data = np.array([10, 14, 20, 22])
mu, sigma = data.mean(), data.std()
print(f'平均: {mu}, 標準偏差: {sigma}')

x = np.linspace(-30, 30 , 100)
y1 = normal_distribution(x, 0, 1) # 平均0, 標準偏差1の正規分布(標準正規分布)
y2 = normal_distribution(x, 5, 5) # 平均5, 標準偏差5の正規分布
y3 = normal_distribution(x, 16.5, 0.5) # 平均16.5, 標準偏差0.5の正規分布
y4 = normal_distribution(x, mu, sigma) # 平均mu, 標準偏差sigmaの正規分布

xs = [x, x, x, x]
ys = [y1, y2, y3, y4]
labels = ["標準正規分布", r'$\mu=5, \sigma=5$', r'$\mu=16.5, \sigma=0.5$', r'$\mu=calc, \sigma=calc$']

fig, axs = plt.subplots(2, 2, figsize=(12, 10), facecolor="w")
axs = axs.ravel()
#データ1
plot_line(xs[0], ys[0], axs[0], labels[0], "x", "y", labels[0], varbose=True)
plot_line(data, np.zeros_like(data), axs[0], 'data', "x", "y", labels[0], varbose=False)
#データ2
plot_line(xs[1], ys[1], axs[1], labels[1], "x", "y", labels[1], varbose=True)
plot_line(data, np.zeros_like(data), axs[1], 'data', "x", "y", labels[1], varbose=False)
#データ3
plot_line(xs[2], ys[2], axs[2], labels[2], "x", "y", labels[2], varbose=True)
plot_line(data, np.zeros_like(data), axs[2], 'data', "x", "y", labels[2], varbose=False)
#データ4
plot_line(xs[3], ys[3], axs[3], labels[3], "x", "y", labels[3], varbose=True)
plot_line(data, np.zeros_like(data), axs[3], 'data', "x", "y", labels[3], varbose=False)

print(rf'$\mu=0, \sigma=1$の尤度 : {calc_likelihood(data, 0, 1):.10f}')
print(rf'$\mu=5, \sigma=5$の尤度 : {calc_likelihood(data, 5, 5):.10f}')
print(rf'$\mu=16.5, \sigma=0.5$の尤度 : {calc_likelihood(data, 16.5, 0.5):.10f}')
print(rf'$\mu=calc, \sigma=calc$の尤度 : {calc_likelihood(data, mu, sigma):.10f}')

[OUT]
平均: 16.5, 標準偏差: 4.769696007084728
$\mu=0, \sigma=1$の尤度 : 0.0000000000
$\mu=5, \sigma=5$の尤度 : 0.0000000002
$\mu=16.5, \sigma=0.5$の尤度 : 0.0000000000
$\mu=calc, \sigma=calc$の尤度 : 0.0000066235

（図は上に記載）

　この尤もらしさを関数で表現したのが尤度（尤度関数）$${L}$$です。複数データの場合は各尤度（正規分布）の総乗となります。なお正規分布の縦軸は確率密度であり正規分布の中心ほどデータの出やすさが大きくなるため、尤度が最大（全データが同時に出現確率が最大）のパラメータが最適なパラメータとなります。

$$
L(\mu, \sigma) = \prod_{i=1}^n f(x) = \prod_{i=1}^n \dfrac{1}{\sqrt{2\pi\sigma^2}}\exp(-\dfrac{(x-\mu)^ 2}{2\sigma^ 2})
$$

６－３．単回帰のモデル設計：誤差項と尤度関数

　単回帰のモデルを傾き$${a}$$, 切片$${b}$$として考えますが、これに$${\epsilon}$$を追加します。$${\epsilon}$$は誤差項（モデルのばらつき）です。

$$
y_i = ax_i + b + \epsilon_i
$$

　ここで誤差項$${\epsilon}$$は平均0, 分散$${\sigma^ 2}$$の正規分布に従うと仮定します。この誤差は$${y_i = ax_i + b + \epsilon_i}$$でのばらつきであるため、推論値を中心とする正規分布となります（追って可視化します）。

$$
\epsilon_i \sim N(0, \sigma^2)=f(\epsilon_i)=\dfrac{1}{\sqrt{2\pi\sigma^2}}\exp(-\dfrac{\epsilon_{i}^ 2}{2\sigma^ 2})
$$

　単回帰モデルを$${\epsilon_i=y_i -(ax_i + b)}$$に変形して正規分布$${f(\epsilon_i)}$$に代入すると各データにおける確率密度関数（正規分布）$${f(y_i)}$$が得られます。

$$
f(y_i) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left( -\frac{(y_i - (ax_i + b))^2}{2\sigma^2} \right)
$$

　確率密度関数$${f(y_i)}$$を尤度とすると、パラメータ$${a}$$, $${b}$$を用いて尤度関数$${L(a,b)}$$は下記の通り表せます。

$$
L(a, b) = \prod_{i=1}^n f(y_i)
$$

　最後に計算しやすいように対数を取り対数尤度を取得します。

$$
\log L(a, b) = -\frac{n}{2} \log(2 \pi \sigma^2) - \frac{1}{2\sigma^2}\sum_{i=1}^{n} (y_i - (ax_i + b))^2
$$

６－４．誤差項εの確率

　最尤推定は「尤度関数を最大化するパラメータを推定」するため、今回の例では「誤差項εの確率が最大となるパラメータを推定」することになります。ここで理解しにくい”誤差項εの確率が最大”について説明します。
　まずは結論となるイメージ図を紹介します。

　単回帰モデル：$${y_i = ax_i + b + \epsilon_i}$$の誤差項$${ \epsilon_i}$$はデータのばらつきやノイズを表現する役割を果たしており、そのばらつきの確率モデルを正規分布として表現しています。
　推論値$${y_i}$$のばらつき（分布）内にデータ$${t_i}$$が存在すれば”分布内にデータが存在する確率（密度分布）が高い->尤度が大きい”ことになります。各データにおける確率の積を取り、それが最大になるということは「推論値$${y_i}$$で想定したばらつき・ノイズ$${ \epsilon_i}$$にデータ$${t_i}$$が（同時に）存在する確率が最も高い」ことになります。
　つまりデータに対して尤もらしいことを表現しており、尤度関数が最大になるパラメータを見つける（最尤推定）ことで最適なパラメータを決定できます。

　推論値のばらつきの分布$${f(\epsilon_i)}$$が単回帰モデルやデータに対してどのように存在しているのかを可視化するコードを記載しました。なお単回帰モデルのパラメータは最適値を使用しており、かつ上図の分布に塗りつぶしを加えて更に分布が分かりやすいように表現しました。

[IN]
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from typing import Tuple
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.mplot3d.art3d import Poly3DCollection

def plot_data_and_normal_distribution_3D(x_data: np.ndarray, y_data: np.ndarray, slope: float, intercept: float, sigma: float) -> None:
    # 3Dプロットの準備
    fig = plt.figure()
    ax = fig.add_subplot(111, projection='3d')

    # 観測データを散布図でプロット
    for i, (x, y) in enumerate(zip(x_data, y_data)):
        ax.scatter(x, y, 0, color='red', edgecolor='black', linewidth=1, zorder=10)
        ax.text(x, y, 0, f'({x:.3f}, {y:.1f})', fontsize=5)

    # 線形回帰モデルのパラメータを用いて、回帰直線を表示
    y_preds = slope*x_data + intercept #y=ax+b
    ax.plot(x_data, y_preds, np.zeros_like(x_data), color='red', linewidth=0.5, ls = '--')

    #各データポイントにおける正規分布(誤差項ε)を表示
    for i in range(len(x_data)):
        y_pred = slope * x_data[i] + intercept
        y_normal = np.linspace(y_pred-4*sigma, y_pred+4*sigma, 100) #正規分布の横軸(y軸)
        z_normal = norm.pdf(y_normal, loc=y_pred, scale=sigma) #正規分布の確率密度関数
        ax.plot(np.full_like(y_normal, x_data[i]), y_normal, z_normal, color='blue') #正規分布をyz平面で青でプロット
        
        #正規分布の頂点表示：単回帰の線上に薄い青色の線を引く
        ax.plot([x_data[i], x_data[i]], [y_preds[i], slope * x_data[i] + intercept], [0, np.max(z_normal)], color='blue', alpha=0.5, lw=0.3, ls='--')

        # 正規分布（誤差項）をyz平面で薄い青で塗りつぶす
        verts = [list(zip(np.full_like(y_normal, x_data[i]), y_normal, z_normal))]
        ax.add_collection3d(Poly3DCollection(verts, facecolors='blue', edgecolors='blue', alpha=0.1))

    ax.set_xlabel('s5', fontsize=10)
    ax.set_ylabel('target(diabetes)', fontsize=10)
    ax.set_zlabel(r'誤差項\epsilonの確率密度関数', fontsize=10)
    ax.tick_params(labelsize=6)

    plt.show()

# データ
x_data = x_train.values.ravel() #dataframe->np.arrayから1次元配列に変換
y_data = y_train #コピー

# 最小二乗法を用いて線形回帰モデルのパラメータを計算
slope, intercept = np.polyfit(x_data, y_data, 1)
print(f'単回帰の傾き: {slope:.3f}, 切片: {intercept:.3f}')

# 散布図と各データポイントにおける正規分布を表示
sigma = 20 #標準偏差を仮定(適当に設定)
plot_data_and_normal_distribution_3D(x_data, y_data, slope, intercept, sigma)


[OUT]
単回帰の傾き: 1020.851, 切片: 173.104

　結果を見ると左から４つ目のデータは推論値のばらつき（誤差項）に対して大きくずれておりますがそれ以外は軒並み分布の中央に近いことが確認できます。よって各データの確率密度（尤度）が高く、尤度関数（尤度の総乗）が最大化され、パラメータとして尤もらしいことが確認できます。

６－５．最尤推定による解析解の計算

　求めた対数尤度関数を微分することで最適解を求めます。結論として最小二乗法と最尤推定で得られる最適パラメータは同じになります。

$$
\log L(a, b) = -\frac{n}{2} \log(2 \pi \sigma^2) - \frac{1}{2\sigma^2}\sum_{i=1}^{n} (y_i - (ax_i + b))^2
$$

　対数尤度関数を微分します。

$$
\begin{aligned}
 \frac{\partial \log L(a, b)}{\partial a} = \frac{1}{\sigma^2} \sum_{i=1}^n x_i (y_i - (ax_i + b))=0 \\
\frac{\partial \log L(a, b)}{\partial b} = \frac{1}{\sigma^2} \sum_{i=1}^n (y_i - (ax_i + b))=0
\end{aligned}
$$

　偏微分$${ \frac{\partial \log L(a, b)}{\partial a} }$$, $${\frac{\partial \log L(a, b)}{\partial b}}$$の連立方程式を解きます。

$$
\begin{cases}
\sum_{i=1}^n x_i (y_i - (ax_i + b)) =\sum_{i=1}^nx_iy_i -a\sum_{i=1}^nx_i^2 -b\sum_{i=1}^nx_i= 0 \\
\sum_{i=1}^n (y_i - (ax_i + b)) =\sum_{i=1}^ny_i-a\sum_{i=1}^nx_i-nb =0
\end{cases}
$$

よって最適解は下記の通りです。

$$
a = \frac{n\sum_{i=1}^n x_i y_i - (\sum_{i=1}^n x_i)(\sum_{i=1}^n y_i)}{n\sum_{i=1}^n x_i^2 - (\sum_{i=1}^n x_i)^2}
$$

$$
b = \frac{(\sum_{i=1}^n y_i)\sum_{i=1}^n x_i^2 - (\sum_{i=1}^n x_i y_i)(\sum_{i=1}^n x_i)}{n\sum_{i=1}^n x_i^2 - (\sum_{i=1}^n x_i)^2}
$$

---

参考資料

Pythonライブラリ（機械学習・AI）｜KIYO｜note

今後の教材用

リッジ回帰とラッソ回帰の理論と実装を初めから丁寧に - Qiita

最短でリッジ回帰とラッソ回帰を説明（機械学習の学習 #3） - Qiita

線形回帰の過学習を抑えよう ～Ridge回帰とLasso回帰～ | Nature Insight ネイチャーインサイト株式会社

はじめに — 機械学習帳

あとがき

　目標は３月中に全部作成したい。