
Pythonフレームワーク:Torchvision CNNによる画像処理モデル
1.概要
別記事ではPytorchの基本操作やモデル作成方法を記載しました。本記事では画像処理がメインである"Torchvision"に関して紹介していきます。
2.事前の学習ポイント・注意点
2-1.環境構築
基本的にはPytorchインストール時に一緒にインストールされると思います。ライブラリがない場合は手動で追加します。
[Terminal]
pip install torchvision2-2.学習モデル作成時の注意点
学習モデル作成時の注意点・ポイントを紹介します。
【Torchvision(Pytorch)の実装】
NNでは入力値が「0~1」または「-1~1」で高性能となる。よって入力値は標準化や正規化などの前処理をした方がよい
入力値の型式はfloat32にすること。Numpy型からテンソルを作成するとfloat64になるためそのままだとエラーになる。
モデルの重みwは拡張しやすいように行列形状[r, c]であり1つのwでも[1,1]となる。行列計算ができるように入力値の形状を重みに合わせる必要がある(1つのwの場合入力値の形状は(N, 1)が正。(N, )だとエラー)。
ラベルデータ(正解値)の形状も行列形状のため(N, 1)にする必要がある。また分類問題の時は整数(int)が必要な時があるため注意(tensor.long()で変換)
勾配情報を持つパラメータは直接更新できないため"torch.no_grad()"か"最適化関数"を使用する
パラメータ更新後に勾配情報は自動的に0にならないため”初期化(0にする)”処理が必要
メソッドの後ろに"_"があるものは"変数の上書き"を意味している。
【モデル作成】
学習時は「学習(train), 検証(val), テスト(test)」用のデータに分割すべき
決定木と異なり全結合ではNoneは受け付けないため欠損値処理は必要
後で再現性がとれるように乱数値もロギングしておいた方がよい。
深層学習(全結合)=「特徴量をすべてモデルが抽出して最強」のイメージがあったが比較的ハイパーパラメータが多く(学習率η、ノード数、レイヤ数、過学習防止(dropout, norm)など)、かつ特徴量エンジニアリング(入力するデータの整理)の影響も大きいため万能ではない。
3.画像処理における画像データの理解
画像を処理できるライブラリは下記がありますがTorchvision特有の処理があるためデータの理解が必要です。
PIllow(PIL)
OpenCV
Numpy
Torchvision
説明用として各種ライブラリで画像データ取得しておきます。
[IN]
import torchvision
import torchvision.transforms as Trans
from PIL import Image
import numpy as np
import cv2
path_img = 'konan.JPG'
img = Image.open(path_img) #PIL形式
img_np = np.array(img) #numpy形式
img_cv = cv2.imread(path_img) #OpenCV形式
img_tensor = Trans.ToTensor()(img) #torch.Tensor形式
3-1.データの配列
データの配列は下記の通りです。
[IN]
print('PIL:', type(img), img.size, img.mode, img.format) #PILサイズは(幅, 高さ)
print('Numpy:', type(img_np), img_np.shape) #ndarrayは(高さ, 幅, チャネル数) #チャネル数はRGB
print('OpenCV:', type(img_cv), img_cv.shape) #Numpyと形状は同じだが、チャネル数がBGR順
print('Tensor(1データ):', type(img_tensor), img_tensor.shape) #torch.Tensorは(チャネル数, 高さ, 幅)
print('Tensor(複数データ):', type(img_tensor.unsqueeze(0)), img_tensor.unsqueeze(0).shape) #torch.Tensorは(データ数(batch数), チャネル数, 高さ, 幅)
[OUT]
PIL: <class 'PIL.JpegImagePlugin.JpegImageFile'> (484, 648) RGB JPEG
Numpy: <class 'numpy.ndarray'> (648, 484, 3)
OpenCV: <class 'numpy.ndarray'> (648, 484, 3)
Tensor(1データ): <class 'torch.Tensor'> torch.Size([3, 648, 484])
Tensor(複数データ): <class 'torch.Tensor'> torch.Size([1, 3, 648, 484])$$
PIL =Width×Hight (RGB)\\
Numpy =Height×Width×チャネル数(RGB)\\
OpenCV =Height×Width×チャネル数(BGR)\\
TorchVision=チャネル数×Height×Width
$$

torchvisionはtensorを処理するライブラリのためNumpy型を処理しても正しい結果が得られないことは注意が必要です。
3-2.画像データの情報量と正規化
画像はPixcel(画素)のまとまりであり1pixel=1byte(8bit)の情報量を持つ。8bitは(0,1)が8つ並ぶため下記の通り256通りです。画像は1byteを整数値として持つため0~255のデータで構成されます。
$$
1byte=8bit=2^8=256通り(0~255)
$$
深層学習では入力値が0~1の方が学習しやすいため正規化されていない場合は$${\frac{1}{255}}$$をかける必要があります。なおToTensor()メソッドで作成したtensorは自動的に正規化されるため前処理は不要です。
[IN]
print('(Min,Max)_Numpy=', (img_np.min(), img_np.max()), '(Min,Max)_tensor=', (img_tensor.min(), img_tensor.max()))
[OUT]
(Min,Max)_Numpy= (0, 255) (Min,Max)_tensor= (tensor(0.), tensor(1.))4.データの前処理:transforms
データ前処理およびデータ拡張に関する詳細は下記記事に記載しました。その中でよく使う奴だけ抜粋しました。
4-1.データのtensor化
PIL形式の画像をtensorに変換する場合は"ToTensor()"を使用します。このメソッドでは処理と同時に正規化(min=0, max=1)も処理されます。
[IN]
import matplotlib.pyplot as plt
import numpy as np
import torchvision
import torchvision.transforms as Trans
from PIL import Image
path_img = 'konan.JPG'
img_PIL = Image.open(path_img) #PIL形式でファイルを開く
print('PIL形式:', type(img_PIL), img_PIL.size, img_PIL.mode, img_PIL.format) #PILサイズは(幅, 高さ)
Totensor = Trans.ToTensor() #オブジェクト作成
img = Totensor(img_PIL) #torch型に変換
print('Tenso:', type(img), img.shape, f'(Min,Max)={img.min(),img.max()}') #torch.Tensorは(チャネル数, 高さ, 幅)
[OUT]
PIL形式: <class 'PIL.JpegImagePlugin.JpegImageFile'> (484, 648) RGB JPEG
Tensor: <class 'torch.Tensor'> torch.Size([3, 648, 484]) (Min,Max)=(tensor(0.), tensor(1.))参考までに上記も含めてメソッド一覧を紹介します。
【データ形式の変換】
●ToPILImage([mode]):テンソルやnumpy配列をPIL形式に変換
●ToTensor():Pytorchのテンソルに変換+自動で正規化
●PILToTensor():Pytorchのテンソルに変換(正規化はなし)
[IN]
ToPILImage = Trans.ToPILImage() #Tensor->PIL
ToPILToTensor = Trans.PILToTensor() #PIL->Tensor
img_toPIL = ToPILImage(img) #TensorをPILに変換
print('img_toPIL:', type(img_toPIL), img_toPIL.size, img_toPIL.mode, img_toPIL.format) #PILサイズは(幅, 高さ)
img_tensor = ToPILToTensor(img_PIL) #PILをTensorに変換
print('img_tensor:', type(img_tensor), img_tensor.shape, f'(Min,Max)={img_tensor.min(),img_tensor.max()}') #torch.Tensorは(チャネル数, 高さ, 幅)
[OUT]
img_toPIL: <class 'PIL.Image.Image'> (484, 648) RGB None
img_tensor: <class 'torch.Tensor'> torch.Size([3, 648, 484]) (Min,Max)=(tensor(0, dtype=torch.uint8), tensor(255, dtype=torch.uint8))4-2.前処理のパイプライン化:transforms.Compose
個別の前処理だけでなく複数の前処理を一つの処理のようにまとめる(パイプライン化)には"transforms.Compose"を使用します。記法としてはCompose([<処理1,>, <処理2>・・・])のようにリスト内にメソッドのオブジェクトを渡します。
[IN]
transforms = Trans.Compose([
Trans.ToTensor()
])
img = transform(img_PIL)
print('Tensor:', type(img), img.shape, f'(Min,Max)={img.min(),img.max()}') #torch.Tensorは(チャネル数, 高さ, 幅)
[OUT]
Tensor: <class 'torch.Tensor'> torch.Size([3, 648, 484]) (Min,Max)=(tensor(0.), tensor(1.))4-3.データの正規化:Normalize
前提としてToTensor()処理で正規化(min=0, max=1)となっております。”Normalize(mean, std[, inplace])”はμとσを指定することで下記式の正規化が可能です。
$$
X=\frac{(x-μ)}{σ}=\frac{(元データの値-平均値μ)}{標準偏差σ}\\
$$
$$
(例:)Max=\frac{(1.0-0.5)}{0.5}=1.0
$$
$$
(例:)Min=\frac{(0-0.5)}{0.5}=-1.0
$$
[IN ※コードは参照用]
t = Trans.Compose([
Trans.Normalize(0.5, 0.5)
])
t_std = t(img)
print('Tensor_org:', type(img), img.shape, f'(Min,Max)={img.min(),img.max()}') #torch.Tensorは(チャネル数, 高さ, 幅)
print('Tensor_Std:', type(t_std), t_std.shape, f'(Min,Max)={t_std.min(),t_std.max()}') #torch.Tensorは(チャネル数, 高さ, 幅)
plt.imshow(t_std.permute(1,2,0))
[OUT]
Tensor_org: <class 'torch.Tensor'> torch.Size([3, 648, 484]) (Min,Max)=(tensor(0.), tensor(1.))
Tensor_Std: <class 'torch.Tensor'> torch.Size([3, 648, 484]) (Min,Max)=(tensor(-1.), tensor(1.))4-4.自作関数の追加:Lambda()
transformsのLambda()メソッドより無名関数を使用できるため自作の関数を前処理として追加できます。参考として正規化されたtensorを1byte(255倍)に戻してみました。
[IN]
transforms2 = Trans.Compose([
Trans.ToTensor(),
Trans.Lambda(lambda x: 255*x) #正規化->1byteのデータに戻す
])
img2 = transform2(img_PIL)
print('Tensor:', type(img2), img2.shape, f'(Min,Max)={img2.min(),img2.max()}') #torch.Tensorは(チャネル数, 高さ, 幅)
[OUT]
Tensor: <class 'torch.Tensor'> torch.Size([3, 648, 484]) (Min,Max)=(tensor(0.), tensor(255.))5.画像処理モデルの主要レイヤ
ディープラーニング(DL)の強みの1つとして「自動で特徴量を判別・設計できる」という話があります。テーブルデータ(Irisデータのような表形式構造)ではまだ人の手で特徴量を作成する方が精度が良くなりますが、画像処理ではDLの特徴量生成が非常に優秀です。
本章では画像処理で使用される主要レイヤを紹介します。
5ー1.畳み込み層(Convolution):nn.Conv2d
畳み込み(Convoluttion)に関して説明してきます。参考として用語集を下記に記載しました。
【畳み込みに関する用語】
●特徴マップ(feature map):畳み込み層の入出力データ
●入力特徴マップ:畳み込み層の入力データ
●出力特徴マップ:畳み込み層の出力データ
●フィルター(カーネル):入力画像に対して畳み込み演算(内積)を行うための行列であり、各値は画像モデルの重みwとなる。
●パディング:畳み込み演算後に出力画像のサイズが変化しないように入力データ周囲に固定のデータ(例:0)を埋める処理
●ストライド:フィルターを適用する位置の間隔(フィルターのスライドする距離)
●プーリング:指定(行列)領域を小さくする(ひとまとめ)演算です。Maxプーリングなら指定行列領域の最大値のみ抽出します。
特徴として①パラメータがない、②チャネル数は変化しないです。
●Affineレイヤ:全結合層レイヤと同義
●im2col:(for文を使わず効率的に)畳み込み演算を実行(計算)するために4次元データを2次元の行列に変換する処理(Qiita:im2col徹底理解)
5-1-1.畳み込みの原理説明
本節では原理のみ説明してコードは説明しませんのでご留意ください。
畳み込み(Convolution)とはフィルター(またはカーネル)と呼ばれる行列を入力データに対して内積して得られた値となります。
1次元画像の畳み込み演算のイメージは下記の通りです。なおわかりやすさを考慮してイメージ図のバイアスb=0にしていますが通常はフィルターに対して1つだけ存在しており各計算にバイアスbが加算されます。
$$
入力値(演算部分)=
\begin{pmatrix} x_{11} & x_{12} & x_{13} \\ x_{21} & x_{22} & x_{23} \\ x_{31} & x_{32} & x_{33} \end{pmatrix}
$$
$$
kernel(3×3)=
\begin{pmatrix} w_{11} & w_{12} & w_{13} \\ w_{21} & w_{22} & w_{23} \\ w_{31} & w_{32} & w_{33} \end{pmatrix}
$$
$$
bias(1×1)=
\begin{pmatrix} b\end{pmatrix}
$$
$$
出力= w_{11}x_{11}+w_{12}x_{12}+w_{13}x_{13}+w_{21}x_{21}+w_{22}x_{22}+w_{23}x_{23}+w_{31}x_{31}+w_{32}x_{32}+w_{33}x_{33}+b
$$

[IN]
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torchvision
from torchinfo import summary
tensor = torch.tensor([[[[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[13, 14, 15, 16]]]]).float() #1データ, 1次元(Channel), 4wx4h
print(tensor.shape, end='\n\n')
conv = nn.Conv2d(1, 1, kernel_size=3) #入力チャネル数, 出力チャネル数, カーネルサイズ, stride=1, padding=0,
print('Kernel形状:', conv.weight.shape) #1次元(Channel), 1次元(Channel), 3wx3h
print(conv.weight, end='\n\n')
print('bias形状:', conv.bias.shape) #Kernelが1次元のため形状は(1,1)
print(conv.bias)
#初期値の修正
with torch.no_grad():
conv.weight = torch.nn.Parameter(torch.tensor([[[[1, 0, 0],
[0, 1, 0],
[0, 0, 1]]]]).float()) #Kernelの初期値を修正
conv.bias.zero_() #biasを0に初期化
print('\n畳み込み演算(Conv2d)の出力\n', conv(tensor))
[OUT]
torch.Size([1, 1, 4, 4])
Kernel形状: torch.Size([1, 1, 3, 3])
Parameter containing:
tensor([[[[-0.1866, -0.1990, 0.0512],
[ 0.1021, 0.0316, -0.1360],
[ 0.0855, 0.1080, 0.0421]]]], requires_grad=True)
bias形状: torch.Size([1])
Parameter containing:
tensor([-0.0503], requires_grad=True)
畳み込み演算(Conv2d)の出力
tensor([[[[18., 21.],
[30., 33.]]]], grad_fn=<ThnnConv2DBackward>)カーネルによる画像の特徴量抽出のイメージとして下記サイトを参考にしました。下図の通り横に重みが並べば横方向、縦なら縦(シマウマっぽい)の特徴量が抽出できます。深層学習ではこの特徴量を学習によりAIが最適化してくれるため高精度のモデルができます。

3次元(画像データ)適用時も処理は同じですが注意点は下記の通りです。
nn.Conv2dは入力tensor形状を$${Batch数×Channel×Height×Width}$$で想定しているためそれに合わせた形状にすること
kernelの次元=入力画像(または特徴量マップ)の次元と同じになる
出力のチャネル数=kernel数となる。下図にイメージ図を示すがkernelが8枚あるなら出力特徴量マップの次元は8次元になる

【コラム:フィルターによる処理の種類】
前述の通り使用するフィルタ(カーネル)により出力される画像は特徴的になりますが特定のものには名称があります。


5-1-2.畳み込みの引数:パディング、ストライド
ストライドはカーネルをずらす行列数でありデフォルトは1です。パディングに関しては入力値の外周を数値(0)で埋める処理です。
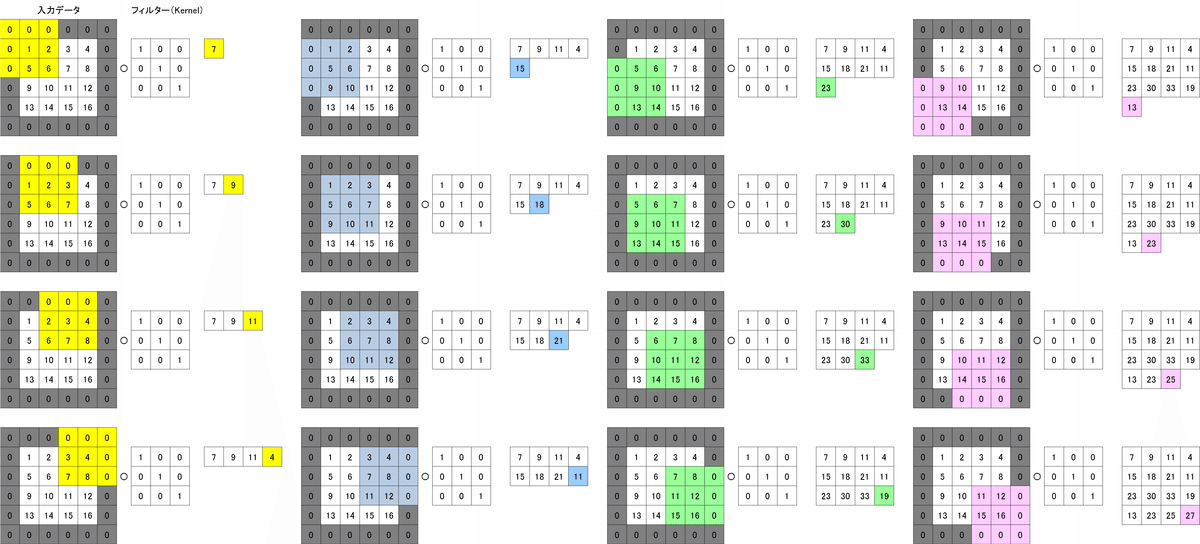
[IN]
conv_pad = nn.Conv2d(1, 1, kernel_size=3, padding=1)
print(conv_pad.weight.shape, conv_pad.bias.shape) #Paddingでもparameter形状は変化なし
with torch.no_grad():
conv_pad.weight = torch.nn.Parameter(torch.tensor([[[[1, 0, 0],
[0, 1, 0],
[0, 0, 1]]]]).float()) #Kernelの初期値を修正
conv_pad.bias.zero_() #biasを0に初期化
print('\n畳み込み演算(Conv2d)_Paddingの出力\n', conv_pad(tensor))
[OUT]
torch.Size([1, 1, 3, 3]) torch.Size([1])
畳み込み演算(Conv2d)_Paddingの出力
tensor([[[[ 7., 9., 11., 4.],
[15., 18., 21., 11.],
[23., 30., 33., 19.],
[13., 23., 25., 27.]]]], grad_fn=<ThnnConv2DBackward>)畳み込み演算を実施すると出力データ形状は下記のように変化します。入力と出力の形状を合わせたい場合などにパディングで調整します。
$$
出力Height=\frac{入力Height+2×Padding-filter size}{Stride}+1
$$
$$
出力Width=\frac{入力Width+2×Padding-filter size}{Stride}+1
$$
5-1-3.畳み込みのコード:nn.Conv2d
nn.Conv2dのコード及びポイントは下記の通りです。
入力必須はin_channels, out_channels, kernel_sizeでありすべてint型
Kernelの形状は(out_channels, in_channels, kernel_size, kernel_size, )となる。つまり(kernel数, channel(次元数), height, width)である。
畳み込み演算をかけるTensorの形状は$${Batch数×Channel×Height×Width}$$とすること
torch.nn.Conv2d(in_channels, out_channels, kernel_size,
stride=1, padding=0, dilation=1, groups=1,
bias=True, padding_mode='zeros', device=None, dtype=None)【Parameters】
●in_channels (int):入力画像のチャネル数(次元数)
●out_channels (int):畳み込み演算で出力される特徴量マップのチャネル数
●kernel_size (int or tuple):フィルター(kernel)のサイズ(height, width)
●stride (int or tuple, optional):ストライド( Default: 1)
●padding (int, tuple or str, optional):四隅にいれるPaddingの数(Default: 0)
※下記は普段使用しないため原文のみ
●padding_mode (string, optional):'zeros', 'reflect', 'replicate' or 'circular'. Default: 'zeros'
●dilation{Default: 1}:膨張畳み込み向けに、カーネルの間隔を指定
●groups (int, optional):Number of blocked connections from input channels to output channels. Default: 1
●bias (bool, optional):If True, adds a learnable bias to the output. Default: True
5-1-4.膨張畳み込み(Dilated Convolution)
畳み込みの特殊版として膨張畳み込み(Dilated Convolution)があります。通常はカーネル間はくっついておりますが、各値の間に隙間を空けて畳み込みする手法になります(動作は下図参照)。
実装は”nn.Conv2(dilation=<隙間サイズ>)”で実装可能です。
[IN]
tensor = torch.tensor([[[[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[13, 14, 15, 16]]]]).float() #1データ, 1次元(Channel), 4wx4h
conv_dilated = nn.Conv2d(1, 1,
kernel_size=3,
padding=1,
dilation=2) #stride=2で出力サイズは2x2になる
#parameterの初期値(参考用)
with torch.no_grad():
conv_dilated.weight = torch.nn.Parameter(torch.tensor([[[[1, 0, 0],
[0, 1, 0],
[0, 0, 1]]]]).float()) #Kernelの初期値を修正
conv_dilated.bias.zero_() #biasを0に初期化
print('畳み込み演算(Conv2d)_Dilatedの出力\n', conv_dilated(tensor))
[OUT]
畳み込み演算(Conv2d)_Dilatedの出力
tensor([[[[22., 7.],
[10., 12.]]]], grad_fn=<SlowConvDilated2DBackward>)
5ー2.プーリング層(Pooling)
Poolingは行列方向の空間を小さくする演算であり下記特徴がある。
学習するパラメータがない
チャネル数は変化しない
行列方向のサイズはPooling領域(size)に合わせて圧縮される
(主にMax Pooliingでは)ある枠内における特徴的な数値を抽出するため画像のブレに強い(絵がずれてもPoolingで特徴を吸収してくれる)。

[IN]
import torch
import torch.nn.functional as F
tensor = torch.tensor([[[[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[13, 14, 15, 16]]]]).float() #1データ, 1次元(Channel), 4wx4h
F.max_pool2d(tensor, kernel_size=2)
[OUT]
tensor([[[[ 6., 8.],
[14., 16.]]]])Maxpoolingのコードは下記の通り、基本的にはkernel_size(pooling領域)を指定すれば使用できます。
torch.nn.functional.max_pool2d(input, kernel_size, stride=None,
padding=0, dilation=1,
ceil_mode=False, return_indices=False)【Parameters】
●input:処理するTensor(画像データ)
●kernel_size:プーリング領域のサイズ。タプル(kH, kW)も受付可能
●stride:プーリングのストライド(Default: kernel_size)
※下記は普段使用しないため原文のみ
●padding:Implicit negative infinity padding to be added on both sides, must be >= 0 and <= kernel_size / 2.
●dilation:The stride between elements within a sliding window, must be > 0.
●ceil_mode:If True, will use ceil instead of floor to compute the output shape. This ensures that every element in the input tensor is covered by a sliding window.
●return_indices:If True, will return the argmax along with the max values. Useful for torch.nn.functional.max_unpool2d later
【参考:F.adaptive_avg_pool2d】
チャネル数(次元数)は変更せずに指定した(Width, Hight)にあうようにフィルター領域を調整してPoolingする機能として"adaptive_xxx_pool2d"があります。参考として平均値avgをとる処理を紹介します。
[IN]
import torch
import torch.nn.functional as F
tensor = torch.tensor([[[[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[13, 14, 15, 16]]]]).float() #torch.Size([1, 1, 4, 4])※1データ, 1次元(Channel), 4wx4h
t1 = F.adaptive_avg_pool2d(tensor, (1, 1)) #torch.Size([1, 1, 1, 1])
t2 = F.adaptive_avg_pool2d(tensor, (2, 2)) #torch.Size([1, 1, 2, 2])
t3 = F.adaptive_avg_pool2d(tensor, (3, 3)) #torch.Size([1, 1, 3, 3])
t4 = F.adaptive_avg_pool2d(tensor, (4, 4)) #torch.Size([1, 1, 4, 4])
print(t1, t1.shape) #1x1に変換
print(t2, t2.shape) #1x1に変換
print(t3, t3.shape) #1x1に変換
print(t4, t4.shape) #1x1に変換
[OUT]
tensor([[[[8.5000]]]]) torch.Size([1, 1, 1, 1])
tensor([[[[ 3.5000, 5.5000],
[11.5000, 13.5000]]]]) torch.Size([1, 1, 2, 2])
tensor([[[[ 3.5000, 4.5000, 5.5000],
[ 7.5000, 8.5000, 9.5000],
[11.5000, 12.5000, 13.5000]]]]) torch.Size([1, 1, 3, 3])
tensor([[[[ 1., 2., 3., 4.],
[ 5., 6., 7., 8.],
[ 9., 10., 11., 12.],
[13., 14., 15., 16.]]]]) torch.Size([1, 1, 4, 4])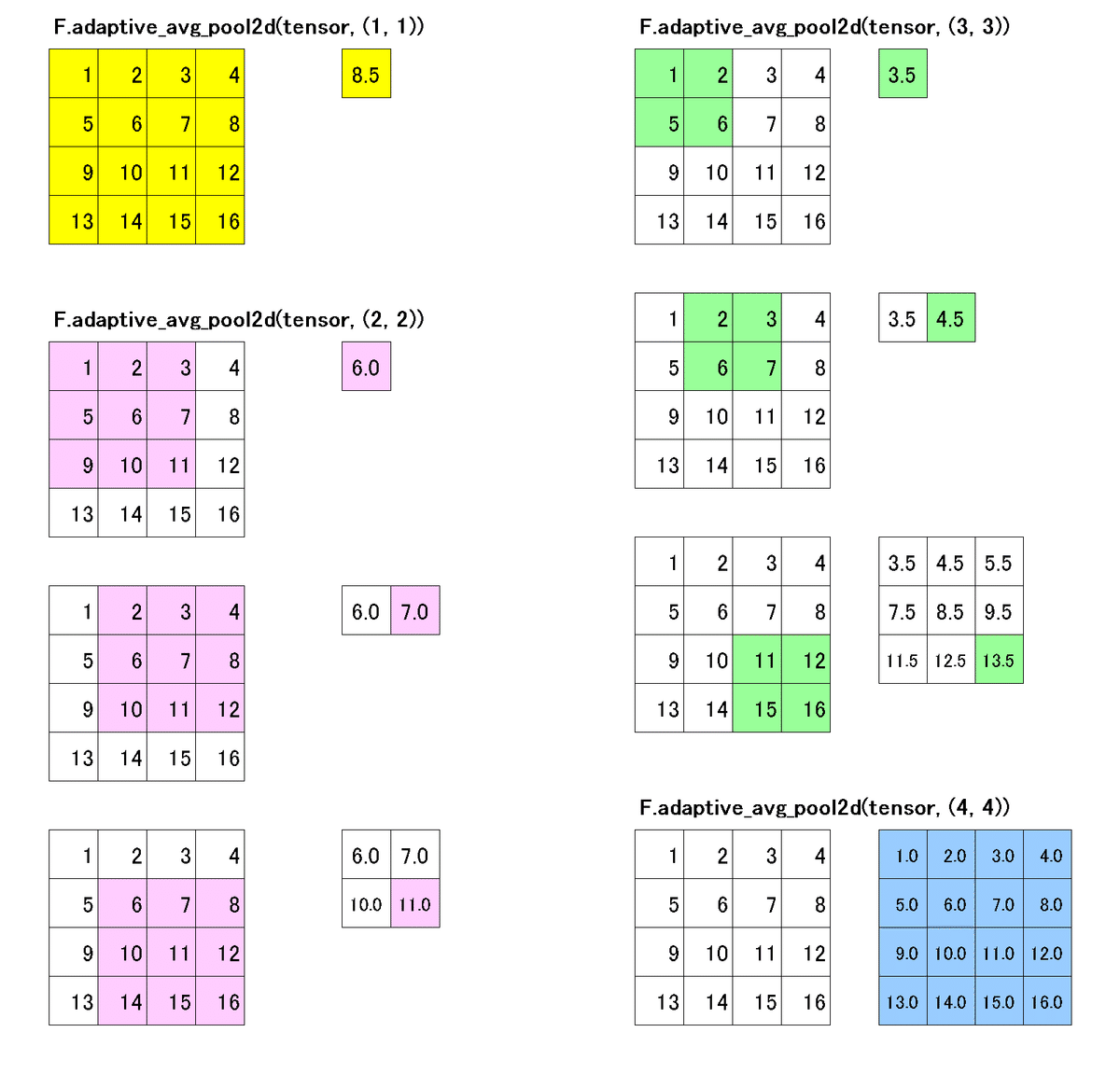
5ー3.全結合層化層(Flatten)
画像データから分類モデルを作成する場合、ラベルがカテゴリカルデータになるため出力は行列となるため、どこかで多次元->1階テンソルに変換する必要があります(下図参照)。Flattenは1階テンソル化する処理をします。

参考コードを記載します。nn.Flatten()はtensor.view(-1, c*w*h)で代用可能(-1=データ数になる)だが、レイヤとしてわかりやすいため紹介します。
[IN]
tensor = torch.tensor([[[[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[13, 14, 15, 16]]]]).float() #1データ, 1次元(Channel), 4wx4h
print(tensor.shape)
flatten = nn.Flatten()
tensor_flat = flatten(tensor)
print(tensor_flat.shape)
print(tensor.view(-1, 1*4*4).shape)
[OUT]
torch.Size([1, 1, 4, 4])
torch.Size([1, 16])
torch.Size([1, 16])コードは下記の通り基本的には引数は気にせずそのまま使用できます。
torch.nn.Flatten(start_dim=1, end_dim=- 1)【Paramters】
●start_dim:first dim to flatten (default = 1).
●end_dim:last dim to flatten (default = -1)
【コラム:Softmax関数に関して】
分類問題のとき「順伝搬の時にSoftmax関数が必要」という説明があります。これらのポイントは下記の通りです。
分類ではよく公差エントロピー(CE)が使用される。このCEには確率pが必要であり、pがないと誤差逆伝搬が使えず学習できない
Softmax関数の特性として高い値ほど高い確率がでます。検証(学習が不要)時は「最も確率が高い分類はどれか」が分かればよいためSoftmaxの計算は不要
上記を考慮すると回帰ではsoftmaxは不要
$$
\sigma(z_i) = \frac{e^{z_{i}}}{\sum_{j=1}^K e^{z_{j}}} \ \ \ for\ i=1,2,\dots,K
$$
$$
Binary Cross Entropy(2値分類) = -{(y\log(p) + (1 - y)\log(1 - p))}
$$
$$
Cross Entropy(多値分類) = -\sum_{c=1}^My_{o,c}\log(p_{o,c})
$$
5-4.転置畳み込み(ConvTranspose2d)
転置畳み込みとは特殊な畳み込みで画像サイズを拡大する処理です。通常の畳み込みでは出力画像のサイズは入力と同じかそれ以下になりますが、転置畳み込みでは出力画像のサイズが入力画像より大きくなります。
使用例としてGAN(生成器)のように1次元のベクトルから転置畳み込みで出力を拡大することで画像を生成するような場面で使用します。

詳細は下記記事に作成したのでご参考までに。
6.過学習防止テクニック
過学習防止のテクニックとして①データ側と②モデル側の2つの側面で紹介します。
6ー1.データの水増し(Data Argument)
まず大前提として「より複雑なモデルを使用するなら、より多く・より多様のデータが必要」です。特に自前のデータだと量が十分に取れない場合があるため、自分でデータを加工してデータ量を増やす操作をData Argumentと言います。詳細は別記事にまとめました。
6ー2.ドロップアウト:nn.Dropout
過学習抑制の手法として2014年に発表されたドロップアウトの概要は下記の通りです。
昔は過学習に対してWeight Decay(損失関数に対して重みのL2ノルムを加算する手法)を使用してたがモデルが複雑になるにつれ十分な効果を得られないためドロップアウトへ移行していった。
ドロップアウトとは学習時に順伝搬するノード(ニューロン)をランダムに消去する手法(検証時は全ノードを使用)
一部のニューロンは使用しない=別に学習したモデルが混ざる ことからアンサンブルモデルに似たような効果がある
入力値との全体平均を合わせるため出力値は$${\frac{1}{(1-p)}}$$倍される
過学習防止の反面、学習時間が長くなるデメリットがある
[IN]
tensor = torch.tensor([[[[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[13, 14, 15, 16]]]]).float() #1データ, 1次元(Channel), 4wx4h
dropout = nn.Dropout(p=0.5)
print(dropout(tensor))
print(tensor.mean(), dropout(tensor).mean())
[OUT]
tensor([[[[ 0., 4., 6., 8.],
[ 0., 0., 14., 0.],
[18., 20., 22., 0.],
[ 0., 0., 30., 32.]]]])
tensor(8.5000) tensor(8.7500)(出典:Dropout: A Simple Way to Prevent Neural Networks from Overfitting)
6ー3.バッチ正規化(Batch Normalization)
6-3-1.詳細および数式
過学習抑制の手法として2015年に発表されたBatch Normalizationの概要は下記の通りです。本手法によりDropoutを使わなくても過学習が抑制できるようになってきております。
数式を見ての通り「ミニバッチの入力データを平均0, 分散1に変換することでデータの分布の偏りを減らす」効果があります。
学習を早く進行させることができい(学習係数ηを大きくでき)、初期値にそれほど依存しない
計算ではミニバッチを単位として、ミニバッチごとに正規化(データの分布の平均0, 分散1にする)を行う。
BatchNormはパラメータを持つためnnモジュールから使用
BN関数は自信のパラメータ(γとβ)があり学習の対象である。よってモデル作成時は必ず1つのBNレイヤにつき1個定義する必要がある(一つのレイヤを複数個所に使用できない)。
$$
平均u_{B} = \frac{1}{m} \sum_{i=1}^{m} \textbf{x}^{(i)}
$$
$$
分散 σ^2 = \frac{1}{m} \sum_{i=1}^{m} (\textbf{x}^{(i)} – \mu_{B} )^2
$$
$$
\^{x} _{i} = \frac{\textbf{x}^{(i)} – u_{B}}{\sqrt{\sigma^2 + \epsilon}}
$$
$$
y_{i} = \gamma \ \^{x} _{i} + \beta = \gamma \frac{\textbf{x}^{(i)} – \mu}{\sqrt{\sigma^2 + \epsilon}} + \beta
$$

モジュールの引数や属性は下記の通りです。
torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1,
affine=True, track_running_stats=True,
device=None, dtype=None)【Parameters】
●num_features:入力値 (N, C, H, W)のChannelサイズ
●eps(Default: 1e-5):BatchNorm2d数式内のεであり分散に影響を与えるー>基本的には小さな値による"zerodivisionerror"防止が目的
※γとβは初期値γ=1.0, β=0である。
※下記は難しいので理解し手から追記
●momentum:the value used for the running_mean and running_var computation. Can be set to None for cumulative moving average (i.e. simple average). Default: 0.1
●affine:a boolean value that when set to True, this module has learnable affine parameters. Default: True
●track_running_stats:a boolean value that when set to True, this module tracks the running mean and variance, and when set to False, this module does not track such statistics, and initializes statistics buffers running_mean and running_var as None. When these buffers are None, this module always uses batch statistics. in both training and eval modes. Default: True
計算時のBatchNorm2dのパラメータや統計値は下記で確認できます。
[IN]
print('weight:', bn2d.weight, 'bias:', bn2d.bias)
print('平均:', bn2d.running_mean, '分散:', bn2d.running_var)
[OUT]
weight: Parameter containing:
tensor([1.], requires_grad=True)
bias: Parameter containing:
tensor([0.], requires_grad=True)
平均: tensor([0.8500])
分散: tensor([3.1667])6-3-2.動作検証およびサンプルコード
1次元(Channel)のテンソルのBatchNormは下記の通りです。
[IN]
tensor = torch.tensor([[[[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[13, 14, 15, 16]]]]).float() #1データ, 1次元(Channel), 4wx4h
bn2d = torch.nn.BatchNorm2d(num_features=1, eps=1e-05, momentum=0.1)
tensor_norm = bn2d(tensor)
print('BN処理前形状:', tensor.shape, 'BN処理後形状:', tensor_norm.shape, end='\n\n')
print(tensor_norm)
[OUT]
torch.Size([1, 1, 4, 4]) torch.Size([1, 1, 4, 4])
tensor([[[[-1.6270, -1.4100, -1.1931, -0.9762],
[-0.7593, -0.5423, -0.3254, -0.1085],
[ 0.1085, 0.3254, 0.5423, 0.7593],
[ 0.9762, 1.1931, 1.4100, 1.6270]]]],
grad_fn=<NativeBatchNormBackward>)
3次元(Channel)のテンソルのBatchNormは下記の通りです。
[IN]
tensor = torch.tensor([[[[ 1., 2.],
[ 3., 4.]],
[[ 1., 5.],
[ 10., 15.]],
[[ 1., 10.],
[20., 30.]]]])
bn2d = torch.nn.BatchNorm2d(num_features=3, eps=1e-05, momentum=0.1)
tensor_norm = bn2d(tensor)
print('BN処理前形状:', tensor.shape, 'BN処理後形状:', tensor_norm.shape, end='\n\n')
print(tensor_norm)
print('weight:', bn2d.weight, 'bias:', bn2d.bias)
print('平均:', bn2d.running_mean, '分散:', bn2d.running_var)
[OUT]
BN処理前形状: torch.Size([1, 3, 2, 2]) BN処理後形状: torch.Size([1, 3, 2, 2])
tensor([[[[-1.3416, -0.4472],
[ 0.4472, 1.3416]],
[[-1.2828, -0.5226],
[ 0.4276, 1.3778]],
[[-1.3136, -0.4839],
[ 0.4379, 1.3596]]]], grad_fn=<NativeBatchNormBackward>)
weight: Parameter containing:
tensor([1., 1., 1.], requires_grad=True)
bias: Parameter containing:
tensor([0., 0., 0.], requires_grad=True)
平均: tensor([0.2500, 0.7750, 1.5250])
分散: tensor([ 1.0667, 4.5917, 16.5917])
6ー4.スキップ接続(Shortcut Connection)
画像分類コンペのILSVRCにおいて2015年後半までは学習時に訓練が収束できない(degradation)ため20層より深いモデルは作れませんでした。これは検証データだけでなく訓練データですら性能が低いため過学習の問題ではなく恒等写像ができないからです。
ILSVRC(2015)のResNetにおいて、恒等写像が上手くできるように前の層の入力値を合わせて順伝搬させる手法が開発されておりこれをスキップ接続と言います。

本手法はtorchvisionのモジュール内にはないため自分で実装が必要となります。下記はサンプルコードとなりますが実際は学習済みモデルを使用する方が効率的だと思います。
[IN]
from torchinfo import summary
tensor = torch.tensor([[[[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[13, 14, 15, 16]]]]).float() #1データ, 1次元(Channel), 4wx4h
class Net_skip(nn.Module):
def __init__(self, k_chanel):
super().__init__()
self.conv1 = nn.Conv2d(1, k_chanel, kernel_size=3, padding=1)
self.pooling = nn.MaxPool2d(kernel_size=2)
self.conv2 = nn.Conv2d(k_chanel, 1, kernel_size=3, padding=1)
def forward(self, x):
out = F.relu(self.conv1(x)) #出力(入力と同じ):torch.Size([1, 1, 4, 4])
out = self.pooling(out) #出力:torch.Size([1, 1, 2, 2])
out1 = out #skip connection
out = F.relu(self.conv2(out)) + out1 #出力:torch.Size([1, 1, 2, 2])
return out
net = Net_skip(k_chanel=1)
print(summary(net))
net(tensor)
[OUT]
=================================================================
Layer (type:depth-idx) Param #
=================================================================
Net_skip --
├─Conv2d: 1-1 10
├─MaxPool2d: 1-2 --
├─Conv2d: 1-3 10
=================================================================
Total params: 20
Trainable params: 20
Non-trainable params: 0
=================================================================
tensor([[[[14.4853, 11.7940],
[15.8970, 14.1007]]]], grad_fn=<AddBackward0>)6-5.Early Stopping
Early Stoppint(早終終了)とは過学習を避けるために行う正則化の一種であり学習用(train)に過剰適合して検証用(val)のエラーが大きくなる前に学習を中断する手法です。詳細は別記事にまとめました。

7.学習済みモデルの利用
有名な画像コンペのILSVRCで使用されたモデルや最新研究の画像分類モデルを学習済み(重み有)で使用できます。
【使用可能な分類モデル一覧】
●AlexNet
●ConvNeXt
●DenseNet
●EfficientNet
●EfficientNetV2
●GoogLeNet
●Inception V3
●MNASNet
●MobileNet V2
●MobileNet V3
●RegNet
●ResNet
●ResNeXt
●ShuffleNet V2
●SqueezeNet
●SwinTransformer
●VGG:(Qiita:VGG16アーキテクチャについて知りたい情報を1記事で)
●VisionTransformer
●Wide ResNet
[IN]
from torchvision import models
print([i for i in dir(models) if not i.startswith('_')]) # モデル一覧
[OUT]
['AlexNet', 'DenseNet', 'GoogLeNet', 'GoogLeNetOutputs', 'Inception3', 'InceptionOutputs', 'MNASNet', 'MobileNetV2', 'MobileNetV3', 'ResNet', 'ShuffleNetV2', 'SqueezeNet', 'VGG', 'alexnet', 'densenet', 'densenet121', 'densenet161', 'densenet169', 'densenet201', 'detection', 'googlenet', 'inception', 'inception_v3', 'mnasnet', 'mnasnet0_5', 'mnasnet0_75', 'mnasnet1_0', 'mnasnet1_3', 'mobilenet', 'mobilenet_v2', 'mobilenet_v3_large', 'mobilenet_v3_small', 'mobilenetv2', 'mobilenetv3', 'quantization', 'resnet', 'resnet101', 'resnet152', 'resnet18', 'resnet34', 'resnet50', 'resnext101_32x8d', 'resnext50_32x4d', 'segmentation', 'shufflenet_v2_x0_5', 'shufflenet_v2_x1_0', 'shufflenet_v2_x1_5', 'shufflenet_v2_x2_0', 'shufflenetv2', 'squeezenet', 'squeezenet1_0', 'squeezenet1_1', 'utils', 'vgg', 'vgg11', 'vgg11_bn', 'vgg13', 'vgg13_bn', 'vgg16', 'vgg16_bn', 'vgg19', 'vgg19_bn', 'video', 'wide_resnet101_2', 'wide_resnet50_2']モデルを参照するサイトとして「DownBench」などがあります。
7-1.PytorchHub(参考)
Pytorch1.0から導入されたPytorchHubではGitHub上で公開されたモデルをPytorch上で使える仕組みです。特徴は下記の通りです。
他の人が作成した学習済みモデルを使用できる
GitHubアップロード時(自分でモデルを作成する場合)は"hubconf.py"ファイルが必要->GitHub上で"hubconf.pyを検索すればモデルを探せる
サンプルとして「ALEXNET」を使用してみました。ALEXNETは2012年のImageNetの優勝モデルであり1,000分類の中には猫も入っているためうまく分類できるか確認してみました。

[IN]
import torch
import torchvision
import torchvision.transforms as T
from PIL import Image
model = torch.hub.load('pytorch/vision:v0.10.0', 'alexnet', pretrained=True)
model.eval()
path_img = 'konan.JPG'
img = Image.open(path_img) # PIL image
#PIL画像を前処理:ImageNetに合わせて1.画像サイズ、2.平均と標準偏差で正規化
transforms = T.Compose([
T.Resize((256, 256)), # 画像サイズを256x256に変換
T.ToTensor(), # Tensorに変換
T.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225]), # 平均と標準偏差で正規化
])
y_pred = model(transforms(img).unsqueeze(0)) #画像形状を(3, 256, 256)から(1, 3, 256, 256)に変換
y_pred_idx = torch.max(y_pred, 1)[1] #(1, 1000)から最大値のインデックスを取得
y_pred_idx
[OUT]
tensor([281])「Imagenet Class Index Json」にISLVRCのclass.jsonがあるためindex->カテゴリ名に変換した結果"tabby(トラ猫)"でありうまく分類できてます。
[IN]
import json
with open('imagenet_class_index.json' ,'r') as f:
class_idx_imagenet = json.load(f)
class_idx_imagenet[str(y_pred_idx.item())][1]
[OUT]
'tabby'
7-2.学習済みモデルの読み込み/レイヤ変換
7-2-1.モデルの読み込み:models.<model>
モデルを読み込むにはtorchvision.modelsから選択したいモデルを属性の形で入力します。下記は"vgg16"を使用しました。
[IN]
import pandas as pd
from torchvision import models
from torchinfo import summary
import torch
import torch.nn as nn
model_vgg16 = models.vgg16(pretrained=True) # 学習済みモデルを読み込む
print(model_vgg16)
[OUT]
VGG(
(features): Sequential(
(0): Conv2d(3, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU(inplace=True)
(2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(3): ReLU(inplace=True)
(4): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(5): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(6): ReLU(inplace=True)
(7): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(8): ReLU(inplace=True)
(9): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(10): Conv2d(128, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(11): ReLU(inplace=True)
(12): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(13): ReLU(inplace=True)
(14): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(15): ReLU(inplace=True)
(16): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(17): Conv2d(256, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(18): ReLU(inplace=True)
(19): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(20): ReLU(inplace=True)
(21): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(22): ReLU(inplace=True)
(23): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(24): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(25): ReLU(inplace=True)
(26): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(27): ReLU(inplace=True)
(28): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(29): ReLU(inplace=True)
(30): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
)
(avgpool): AdaptiveAvgPool2d(output_size=(7, 7))
(classifier): Sequential(
(0): Linear(in_features=25088, out_features=4096, bias=True)
(1): ReLU(inplace=True)
(2): Dropout(p=0.5, inplace=False)
(3): Linear(in_features=4096, out_features=4096, bias=True)
(4): ReLU(inplace=True)
(5): Dropout(p=0.5, inplace=False)
(6): Linear(in_features=4096, out_features=1000, bias=True)
)
)
参考までにモデルのsummary()も表示しました。
[IN]
summary(model_vgg16, input_size=(1, 3, 224, 224), device='cpu') # モデルの概要を表示
[OUT]
==========================================================================================
Layer (type:depth-idx) Output Shape Param #
==========================================================================================
VGG -- --
├─Sequential: 1-1 [1, 512, 7, 7] --
│ └─Conv2d: 2-1 [1, 64, 224, 224] 1,792
│ └─ReLU: 2-2 [1, 64, 224, 224] --
│ └─Conv2d: 2-3 [1, 64, 224, 224] 36,928
│ └─ReLU: 2-4 [1, 64, 224, 224] --
│ └─MaxPool2d: 2-5 [1, 64, 112, 112] --
│ └─Conv2d: 2-6 [1, 128, 112, 112] 73,856
│ └─ReLU: 2-7 [1, 128, 112, 112] --
│ └─Conv2d: 2-8 [1, 128, 112, 112] 147,584
│ └─ReLU: 2-9 [1, 128, 112, 112] --
│ └─MaxPool2d: 2-10 [1, 128, 56, 56] --
│ └─Conv2d: 2-11 [1, 256, 56, 56] 295,168
│ └─ReLU: 2-12 [1, 256, 56, 56] --
│ └─Conv2d: 2-13 [1, 256, 56, 56] 590,080
│ └─ReLU: 2-14 [1, 256, 56, 56] --
│ └─Conv2d: 2-15 [1, 256, 56, 56] 590,080
│ └─ReLU: 2-16 [1, 256, 56, 56] --
│ └─MaxPool2d: 2-17 [1, 256, 28, 28] --
│ └─Conv2d: 2-18 [1, 512, 28, 28] 1,180,160
│ └─ReLU: 2-19 [1, 512, 28, 28] --
│ └─Conv2d: 2-20 [1, 512, 28, 28] 2,359,808
│ └─ReLU: 2-21 [1, 512, 28, 28] --
│ └─Conv2d: 2-22 [1, 512, 28, 28] 2,359,808
│ └─ReLU: 2-23 [1, 512, 28, 28] --
│ └─MaxPool2d: 2-24 [1, 512, 14, 14] --
│ └─Conv2d: 2-25 [1, 512, 14, 14] 2,359,808
│ └─ReLU: 2-26 [1, 512, 14, 14] --
│ └─Conv2d: 2-27 [1, 512, 14, 14] 2,359,808
│ └─ReLU: 2-28 [1, 512, 14, 14] --
│ └─Conv2d: 2-29 [1, 512, 14, 14] 2,359,808
│ └─ReLU: 2-30 [1, 512, 14, 14] --
│ └─MaxPool2d: 2-31 [1, 512, 7, 7] --
├─AdaptiveAvgPool2d: 1-2 [1, 512, 7, 7] --
├─Sequential: 1-3 [1, 1000] --
│ └─Linear: 2-32 [1, 4096] 102,764,544
│ └─ReLU: 2-33 [1, 4096] --
│ └─Dropout: 2-34 [1, 4096] --
│ └─Linear: 2-35 [1, 4096] 16,781,312
│ └─ReLU: 2-36 [1, 4096] --
│ └─Dropout: 2-37 [1, 4096] --
│ └─Linear: 2-38 [1, 1000] 4,097,000
==========================================================================================
Total params: 138,357,544
Trainable params: 138,357,544
Non-trainable params: 0
Total mult-adds (G): 15.48
==========================================================================================
Input size (MB): 0.60
Forward/backward pass size (MB): 108.45
Params size (MB): 553.43
Estimated Total Size (MB): 662.49
==========================================================================================7-2-2.レイヤを変換
VGG16はILSVRC用モデルのため最終レイヤは1000次元(1000分類)です。各レイヤやnodesは属性と同じ形で取得できます(nn.Sequential()で作成したレイヤはリストで取得)。
[IN]
_classifier = model_vgg16.classifier
print(_classifier, end='\n\n')
print('List形式で抽出:', _classifier[6])
print('入力nodes:', _classifier[6].in_features, '出力nodes:', _classifier[6].out_features)
[OUT]
Sequential(
(0): Linear(in_features=25088, out_features=4096, bias=True)
(1): ReLU(inplace=True)
(2): Dropout(p=0.5, inplace=False)
(3): Linear(in_features=4096, out_features=4096, bias=True)
(4): ReLU(inplace=True)
(5): Dropout(p=0.5, inplace=False)
(6): Linear(in_features=4096, out_features=1000, bias=True)
)
List形式で抽出: Linear(in_features=4096, out_features=1000, bias=True)
入力nodes: 4096 出力nodes: 1000classifier(Sequential)から最後のLinearを指定して1000分類->2値分類に変更してみます。最後のレイヤ(model_vgg16.classifier[6])のノード(out_features)が1000->2に変換されることが確認できました。
[IN]
model_vgg16.classifier[6] = torch.nn.Linear(_classifier[6].in_features, 2) # 全結合層の出力を2に変更
# print(model_vgg16) # モデル全体の概要を表示
print(model_vgg16.classifier[6])
[OUT]
Linear(in_features=4096, out_features=2, bias=True)【恒等関数:nn.Identity()】
恒等関数(Identity function)とは入力値と出力値が同じ関数($${f(x)=x}$$)であり微分も($${f'(x)=1}$$)のため純伝搬・逆伝搬ともに影響を与えない関数のことです。
例として、モデル内のレイヤを恒等関数に置き換えることでレイヤを削除しなくても同等の動作をさせることが可能です。
[IN]
model_vgg16.classifier[3] = nn.Identity()
model_vgg16.classifier[4] = nn.Identity()
model_vgg16.classifier[5] = nn.Identity()
model_vgg16.classifier[6] = torch.nn.Linear(_classifier[0].out_features, 2) # 全結合層の出力を2に変更
print(model_vgg16)
[OUT]
VGG(
(features): Sequential(
(0): Conv2d(3, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
同上
)
(avgpool): AdaptiveAvgPool2d(output_size=(7, 7))
(classifier): Sequential(
(0): Linear(in_features=25088, out_features=4096, bias=True)
(1): ReLU(inplace=True)
(2): Dropout(p=0.5, inplace=False)
(3): Identity()
(4): Identity()
(5): Identity()
(6): Linear(in_features=4096, out_features=2, bias=True)
)
)7-3.ファインチューニング(全パラメータ更新)
ファインチューニングとは「学習済みモデルの一部もしくはすべての層の重みを微調整する手法」です。
ファインチューニングの実装は下記フローで実施できます。
【ファインチューニングの実装フロー】
1.モデルの選定
2.レイヤの調整:最終層のノード(カテゴリ数)修正、不要なレイヤ削除
3.各レイヤのparamsが勾配を持つ(誤差逆伝搬が可能な状態)ことを確認
4.学習
3.の「勾配を持つ」は各レイヤにおいて”params.requires_grad”で確認できます。下記出力の通り全レイヤで”勾配=True”であり学習可能な状態です。
[IN]
class HorizontalDisplay:
def __init__(self, *args):
self.args = args
def _repr_html_(self):
template = '<div style="float: left; padding: 10px;">{0}</div>'
return "\n".join(template.format(arg._repr_html_())
for arg in self.args)
import pandas as pd
paramslist = []
for name, params in model_vgg16.named_parameters():
paramslist.append([name, params.size(), params.requires_grad])
df = pd.DataFrame(paramslist, columns=['name', 'size', 'requires_grad'])
display(HorizontalDisplay(df.iloc[:11, :], df.iloc[11:21, :], df.iloc[21:, :])) #3列に分割して表示
[OUT]
7-4.転移学習(一部パラメータ更新)
転移学習とは「学習済みモデルの大部分はそのまま使用(再学習させない)して、最後の方の層だけ学習させる」です。
転移学習の実装は下記フローで実施できます。
【転移学習の実装フロー】
1.モデルの選定
2.レイヤの調整:最終層のノード(カテゴリ数)修正、不要なレイヤ削除
3.勾配の設定:学習させたい各レイヤの勾配はTrueにして、学習させないレイヤの勾配はFalseにする
4.学習
3.の「勾配の設定」は「各レイヤのparamsを抽出して.requires_gradをTrue/Falseで設定」します。下記は全結合層(Classifier)のみ学習させるような設定にしました。
[IN]
for name, params in model_vgg16.named_parameters():
if 'classifier' in name: # classifierのパラメータのみrequires_gradをTrueにする
params.requires_grad = True
else:
params.requires_grad = False
paramslist = [[name, params.size(), params.requires_grad] for name, params in model_vgg16.named_parameters()] # パラメータの名前とサイズを取得
df = pd.DataFrame(paramslist, columns=['name', 'size', 'requires_grad'])
display(HorizontalDisplay(df.iloc[:11, :], df.iloc[11:21, :], df.iloc[21:, :])) #3列に分割して表示
[OUT]
8.完成コード
追って(サンプルは下記参照)
別添
別添1:深層学習の特徴を整理
過去の深層学習の経緯を確認しながらモデルには何が重要かを箇条書きにしました。なおソースの一部はAIciaさんのYoutubeを参考にしています。
誤差逆伝搬を使用すれば複雑なモデルでも学習可能
活性化関数にSigmoid関数を使用すると逆伝搬時に勾配消失が起こるけど、ReLUを使うと解消されるため深い層のモデルも使用可能
データはtrain/testデータに分ける必要がある
過学習の抑制にはdropoutが有効(最近はBatchNormalizationも使用):sparse(疎)なパラメータをdense(密)にする
複雑なモデルを使用する場合は大量のデータがないと過学習する
SGD(確率的勾配降下法)は”局所解”になるけど実用的には問題ない。
別添2:サンプルデータ取得:torchvision.datasets
torchvisionのクラス経由でサンプルデータを取得することが可能です。
"torchvision.datasets"を使用してDLでき、引数は下記の通りです。参考として手書き数値のMNIST(学習用:6万枚、テスト用:1万枚)をDLします。ポイントは下記の通りです。
イテラブルなオブジェクトで取得可能(スライスは不可)
②1つのデータは(<data>, <label>)のタプル形式
To.Tensor()の出力値は正規化(Normalization)されておりmax:1, min:0
transform.Compose()を使うことでデータに前処理を加えた出力値も取得可能(例:T.Normalize()による正規化など)
【datasetsの引数】
●root:保存ディレクトリ名を指定(なければ自動で作成される)
●train(True/False):学習用(True)か検証用(False)か
●download(True/False):データが指定フォルダ(root)に存在しないならDL
●transform{defalut:None}:T.ToTensor()を設定することで出力値がPIL形式からtorch.tensor形式になる
[IN]
import torch
import torchvision
import torchvision.datasets as datasets
import torchvision.transforms as T
import japanize_matplotlib
MNISTS_train_PIL = datasets.MNIST(root='./dataset',
train=True, download=True)
M_train_t = datasets.MNIST(root='./dataset',
train=True, download=True, transform=T.ToTensor())
#transformのパイプラインを作成
trans1 = T.Compose([
T.ToTensor()
])
M_test_t = datasets.MNIST(root='./dataset',
train=False, download=True, transform=trans1)
print(MNISTS_train_PIL,'\n', M_train_t, '\n', M_test_t, end='\n\n')
print(type(MNISTS_train_PIL), 'データ数:', len(MNISTS_train_PIL), '1番目のデータ:', type(MNISTS_train_PIL[0]), len(MNISTS_train_PIL[0]), type(MNISTS_train_PIL[0][0]), type(MNISTS_train_PIL[0][1]))
print(type(M_train_t), 'データ数:', len(M_train_t), '1番目のデータ:', type(M_train_t[0]), len(M_train_t[0]), type(M_train_t[0][0]), type(M_train_t[0][1]), 'dataのMax/MIN', (M_test_t[0][0].max(), M_test_t[0][0].min()))
print(type(M_test_t), 'データ数:', len(M_test_t), '1番目のデータ:', type(M_test_t[0]), len(M_test_t[0]), type(M_test_t[0][0]), type(M_test_t[0][1]))
#Matplotlibで画像を表示する
for idx in range(10):
img, label = MNISTS_train_PIL[idx]
ax = plt.subplot(2, 5, idx+1) # 2行5列のグラフを作成
ax.imshow(img, cmap='gray') # 画像を表示
ax.set_axis_off() # 軸を消す
ax.set_title(f'正解値: {label}') #
plt.tight_layout()
plt.show()
[OUT]
Dataset MNIST
Number of datapoints: 60000
Root location: ./dataset
Split: Train
Dataset MNIST
Number of datapoints: 60000
Root location: ./dataset
Split: Train
StandardTransform
Transform: ToTensor()
Dataset MNIST
Number of datapoints: 10000
Root location: ./dataset
Split: Test
StandardTransform
Transform: Compose(
ToTensor()
)
<class 'torchvision.datasets.mnist.MNIST'> データ数: 60000 1番目のデータ: <class 'tuple'> 2 <class 'PIL.Image.Image'> <class 'int'>
<class 'torchvision.datasets.mnist.MNIST'> データ数: 60000 1番目のデータ: <class 'tuple'> 2 <class 'torch.Tensor'> <class 'int'> dataのMax/MIN (tensor(1.), tensor(0.))
<class 'torchvision.datasets.mnist.MNIST'> データ数: 10000 1番目のデータ: <class 'tuple'> 2 <class 'torch.Tensor'> <class 'int'>
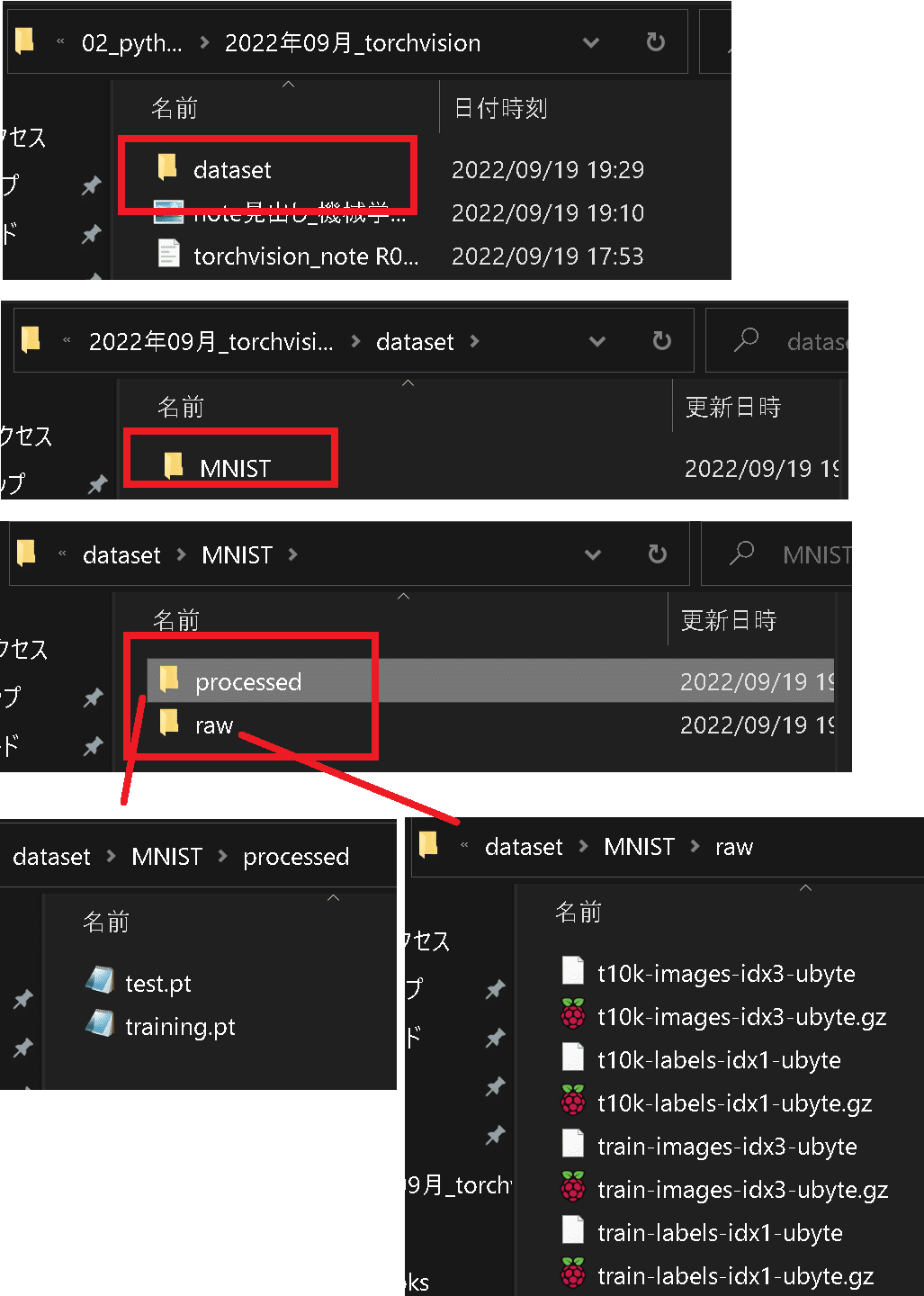
【参考:ダウンロード後のフォルダ構成】
参考資料
資料1:技術
資料2:図示・可視化
https://t.co/eYw6GkUs36
— Kenji Saito (@kenji_special) December 7, 2023
ゼロから作るDeep Learningで学んだ畳み込みニューラルネットワークをリアルタイムに可視化するサイト作りました。https://t.co/4ODfExCdVRと見比べると複雑に見えますが、一つ一つの処理はとてもシンプルです。コードはGitHubに公開してます。https://t.co/KDvZ3or7sx pic.twitter.com/3X6QXzZSds
あとがき
追って追記
最適モデルのサンプルコード作成
Kaggleの練習問題チャレンジ
