
<学習シリーズ>線形モデル編:リッジ回帰・ラッソ回帰
1.概要
1-1.緒言
本記事は”学習シリーズ”として自分の勉強備忘録用になります。
過去の記事で機械学習・AIの記事を多数作成しましたが、シンプルな線形モデルは外挿が比較的得意のためいろんな分野で使用されます。本記事では「リッジ回帰・ラッソ回帰」を学習します。
1-2.用語・記号の説明(全般)
本記事で使用する用語および記号は下記の通りです。
1-2-1.用語一覧
●回帰 (regression):実数値を予測する問題
●分類 (classification):カテゴリ(離散値)を予測する問題
●教師あり学習 (supervised learning):機械学習でデータセットに対して正解値(ラベル)がある学習方法
●教師なし学習 (unsupervised learning):機械学習でデータセットに対して正解値(ラベル)が無い学習方法
●予測値 (predicted value):関数で計算された出力変数y(用語は下記参照)
●目標値 (target value):予測値がとるべき値(教師あり学習の正解値)
●目的関数 (objective function):機械学習において性能の良さの指標を表す関数です。一般的には”予想値と目標値の差異”から作成される関数であり、この関数を最小化することでよいモデルと判断します。
●多重共線性(multicollinearity):多変量解析(重回帰分析など)において、いくつかの説明変数間で線形関係(強い相関関係)があると共線性といい、共線性が複数認められる場合は多重共線性があると言います。
●二乗和誤差 (sum-of-squares error):正解値$${y}$$と予測値$${\hat{y}}$$の差の2乗$${(y-\hat{y})^2}$$です。これをモデルと正解値の誤差とも呼びます。
●最小二乗法:二乗和誤差を最小化することでモデルの当てはまりを最適化する手法です。
1-2-2.記号一覧
●$${f()}$$:$${y=f(x)}$$におけるf()であり関数と呼びます。中身は入力変数xを処理して新しい出力変数yを生成する計算式です。
●$${x}$$:$${y=f(x)}$$におけるxです。複数は下記の通り複数あります。
名称1:説明変数(Explanatory variable)
名称2:独立変数(Independent variable)
名称3:外生変数(Exogenous variable)
名称4:入力変数(Input variable)
名称5:入力値(Input value)
●$${y}$$:$${y=f(x)}$$におけるyです。複数は下記の通り複数あります。
名称1:目的変数(Response variable)
名称2:従属変数(Dependent variable)
名称3:被説明変数(Explained variable)
名称4:内生変数(endogenous variable)
名称5:出力変数(Output variable)
名称6:予測値/推論値(prediction value)
●$${w_i}$$(weight):重み(単回帰の場合は傾きとも言う)
●$${b}$$(bias):バイアス(単回帰の場合は切片とも言う)
1-2-3.ベクトル・行列表記一覧
●M次元の縦ベクトル:$${{\bf x}}$$
$$
\begin{aligned}{\bf x}= \begin{bmatrix} x_{0} \\ x_{1}\\ x_{2} \\ \vdots \\ x_{M} \end{bmatrix} \\ \end{aligned}
$$
●M次元の横ベクトル(縦ベクトルの転置):$${{\bf x}^{\rm T}}$$
$$
\begin{aligned}{\bf x}^{\rm T}= \begin{bmatrix} x_{0} & x_{1}& x_{2} & \dots & x_{M} \end{bmatrix} & \end{aligned}
$$
●N×M次元の行列(M次元をもつN個のデータ):$${{\bf X}}$$
$$
\begin{aligned}
{\bf X} &
= \begin{bmatrix} x_{10} & x_{11} & x_{12} & \cdots & x_{1M} \\
x_{20} & x_{21} & x_{22} & \cdots & x_{2M} \\
x_{30} & x_{31} & x_{32} & \cdots & x_{3M} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\ x_{N0} & x_{N1} & x_{N2} & \cdots & x_{NM} \end{bmatrix}
\end{aligned}
=\begin{bmatrix} {\bf x}_1^{\rm T} \\ {\bf x}_2^{\rm T} \\ {\bf x}_3^{\rm T}\\ \vdots \\ {\bf x}_N^{\rm T} \end{bmatrix}
$$
1-3.サンプル用データ
サンプルデータはScikit-learnの「Boston housing Dataset」を使用します。注意点として古いVersionだとSklearnではPoliticalな理由で使用できないため、代わりに「California housing Dataset」をご利用ください。
データは過学習がしやすいように決定係数が小さくなる乱数でデータ抽出しました。
[IN]
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib
from mpl_toolkits.mplot3d import Axes3D
from sklearn import datasets
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from tqdm import tqdm
from typing import Tuple, List, Dict, Union, Any, Optional
dict_En2Jp = {
"CRIM": "犯罪率",
"ZN": "広い家の割合(25,000ft^2以上)",
"INDUS": "非小売業の割合",
"CHAS": "チャールズ川の隣か",
"NOX": "NOx濃度",
"RM": "平均部屋数",
"AGE": "古い家の割合(1940年)",
"DIS": "主要施設への距離",
"RAD": "主要高速道路へのアクセス性",
"TAX": "固定資産税率(10,000ドル当たり)",
"PTRATIO": "生徒と先生の比率",
"B": "1000(黒人の割合 - 0.63)^2",
"LSTAT": "低所得者人口の割合",
"MEDV": "住宅価格"
}
boston = datasets.load_boston()
data, target = boston.data, boston.target
df_data = pd.DataFrame(data, columns=boston.feature_names)
df_target = pd.DataFrame(target, columns=["MEDV"])
df = pd.concat([df_data, df_target], axis=1)
display(df.rename(columns=dict_En2Jp)) #カラムを日本語に変換して表示
#データ抽出:ランダム
df_2dim = df[["RM", "MEDV"]] #部屋数と住宅価格のみ抽出
np.random.seed(468) #R2Scoreが小さい値になるシード値
idx_rand = np.random.choice(df.index, size=40, replace=False)
df_2dim = df.loc[idx_rand, :]
print(f'抽出後2次元データ:{df_2dim.shape}')
#線形回帰
linear = LinearRegression() #モデル定義
linear.fit(df_2dim[["RM"]], df_2dim["MEDV"]) #学習
y_pred = linear.predict(df_2dim[["RM"]]) #推論
score_r2 = r2_score(df_2dim["MEDV"], y_pred) #決定係数
#データ可視化:2次元
fig, ax = plt.subplots(1, 1, figsize=(10, 6), facecolor='w')
sns.scatterplot(x="RM", y="MEDV", data=df_2dim, ax=ax, label="データ")
ax.plot(df_2dim["RM"], y_pred, color="red", label="線形回帰", lw=1.0)
ax.text(7.0, 30, f"決定係数:{score_r2:.3f}", fontsize=14, color="red")
ax.set(xlabel="部屋数[個]", ylabel="住宅価格[k$]")
ax.grid(), ax.legend()
plt.show()[OUT]
抽出後2次元データ:(40, 14)

2.基礎用語
2-1.ノルム:np.linalg.norm()
ノルムとは「ベクトルの大きさ(距離)」に近い指標でありベクトル$${x}$$をn次元$${x = (x_1,\cdots,x_n)}$$としたときのノルム$${L_{p}}$$は次のように定義されます。
本記事では下記3種のノルムを紹介します。重要なこととして「尺度の異なる数値が組み合われたデータに関する距離の計算は要注意」となります。
$$
{\|\boldsymbol{x}\|_p = \sqrt[p]{|x_1|^p+|x_2|^p+\cdots+|x_n|^p} }
$$
$$
L_{1Norm}(マンハッタン距離) = \sum_{i=1}^{n} |x_i|=|x_{1}|+|x_{2}|+ \dots +|x_{n}|
$$
$$
L_{2Norm}(ユークリッド距離距離) = \sqrt{\sum_{i=1}^{n} x_i^2}=\sqrt{x_{1}^2 + x_{2}^2 + \cdots + x_{n}^2}
$$
【ノルムの種類(参考:高校数学の美しい物語)】
●L0ノルム:ベクトル内における0でない値の数を計算
●L1ノルム(マンハッタン距離):各成分の絶対値の和
●L2ノルム(ユークリッド距離):一般的な距離を意味する。高校数学での三平方の定理でも使われるように長さと同等である。
Numpyでは"np.linalg.norm(<array>, ord=<Norm>)"で計算可能です。
[IN]
A = np.array([[0, 1, -2],
[-3, 4, 5]])
#ベクトルの内積
L0 = np.linalg.norm(A.ravel(), ord=0) #L0ノルム:非ゼロ要素の数※ベクトルのみ
L1 = np.linalg.norm(A.ravel(), ord=1) #L1ノルム:マンハッタン距離
L2 = np.linalg.norm(A.ravel()) #L2ノルム:ユークリッド距離
print(f'L0:{L0:.2f}, L1:{L1:.2f}, L2:{L2:.2f}')
#行列で指定:aixs=0:列方向, axis=1:行方向
L1_ax0 = np.linalg.norm(A, ord=1, axis=0) #L1ノルム:マンハッタン距離
L1_ax1 = np.linalg.norm(A, ord=1, axis=1) #L1ノルム:マンハッタン距離
L2_ax0 = np.linalg.norm(A, ord=2, axis=0) #L2ノルム:ユークリッド距離
L2_ax1 = np.linalg.norm(A, ord=2, axis=1) #L2ノルム:ユークリッド距離
print(f'L1_ax0:{L1_ax0}, L1_ax1:{L1_ax1}, L2_ax0:{L2_ax0}, L2_ax1:{L2_ax1}')
[OUT]
L0:5.00, L1:15.00, L2:7.42
L1_ax0:[3. 5. 7.], L1_ax1:[ 3. 12.], L2_ax0:[3. 4.123 5.385], L2_ax1:[2.236 7.071]$$
A=\begin{bmatrix}0 & 1 & -2 \\-3 & 4 & 5 \\ \end{bmatrix}, A.ravel()=\begin{bmatrix}0 & 1 & -2 &-3 & 4 & 5 \end{bmatrix}
$$
$$
L_{1Norm}=|0|+|1|+|-2|+|-3|+|4|+|5| = 15 \\
L_{2Norm}=\sqrt{0^2 + 1^2 + (-2)^2 + (-3)^2 + 4^2 + 5^2} = \sqrt{55} = 7.42
$$
【コラム:ユークリッド距離の補足(データ間の距離と類似度)】
2-2.単回帰・重回帰
2-2-1.単回帰の数式
単回帰は重回帰における説明変数が1次元のものになります。
$$
単回帰:y = w_{1}x_{1} +b
$$
2-2-2.重回帰の数式
重回帰は各説明変数に重みをかけた値の総和+バイアス項です。
$$
重回帰:y = w_{1}x_{1} + w_{2}x_{2} + \cdots + w_{M}x_{M} + b=\sum_{m=1}^{M} w_{m} x_{m} + b
$$
M次元の入力変数$${x}$$に$${x_0=1}$$を追加してM+1次元とし、同様にM次元の重み$${w}$$に$${w_0=b}$$を追加すると下記へ変換できます。
$$
\begin{aligned} y &
= w_{1}x_{1} + w_{2}x_{2} + \cdots + w_{M}x_{M} + b \\ &
= w_{1}x_{1} + w_{2}x_{2} + \cdots + w_{M}x_{M} + w_{0}x_{0} \\ &
= w_{0}x_{0} + w_{1}x_{1} + \cdots + w_{M}x_{M} \\ &
= \sum_{m=0}^M w_{m} x_{m} \end{aligned}
$$
2-2-3.重回帰を行列に変換
重回帰は多次元のためベクトル・行列で表され、直接解法も行列で計算するため行列式で表現する方が便利となります。
重回帰を重み$${\bf w}$$と説明変数$${\bf x}$$のベクトルの内積で表現するることができます。なお注意点は下記の通りです。
バイアス$${b}$$は$${x_0=1}$$, $${w_0=b}$$より$${w_0x_0=b}$$で存在
バイアス$${b}$$を含むため$${\bf w}$$, $${\bf x}$$共にM+1次元
ベクトル同士の内積を計算するために、重み$${\bf w}$$は転置
【データ数が1個(1行の行列):1×(M+1)行列】
$$
\begin{aligned} y = w_{0}x_{0} + w_{1}x_{1} + \cdots + w_{M}x_{M} = \begin{bmatrix} w_{0} & w_{1} & \cdots & w_{M} \end{bmatrix} \begin{bmatrix} x_{0} \\ x_{1} \\ \vdots \\ x_{M} \end{bmatrix} = {\bf w}^{\rm T}{\bf x}
\end{aligned}
$$
【データ数がN個(N行の行列):(N×(M+1)行列)】
$$
\begin{aligned}{\bf y}&
=\begin{bmatrix} y_1 \\ y_2 \\y_3 \\ \vdots \\ y_N \end{bmatrix}
=\begin{bmatrix}{\bf x}_1^{\rm T}{\bf w} \\{\bf x}_2^{\rm T}{\bf w} \\{\bf x}_3^{\rm T}{\bf w} \\\vdots \\{\bf x}_N^{\rm T}{\bf w}\end{bmatrix}
= \begin{bmatrix}w_{10}x_{10} + w_{11}x_{11} + w_{12}x_{12} + \cdots + w_{1M}x_{1M} \\w_{20}x_{20} + w_{21}x_{21} + w_{22}x_{22} + \cdots + w_{2M}x_{2M} \\ w_{30}x_{30} + w_{31}x_{31} + w_{32}x_{32} + \cdots + w_{3M}x_{3M} \\
\vdots
\\w_{N0}x_{N0} + w_{N1}x_{N1} + w_{N2}x_{N2} + \cdots + w_{NM}x_{NM}\end{bmatrix}\end{aligned}
$$
$$
=\begin{bmatrix}x_{10} & x_{11} & x_{12} & \cdots & x_{1M} \\
x_{20} & x_{21} & x_{22} & \cdots & x_{2M} \\
x_{30} & x_{31} & x_{32} & \cdots & x_{3M} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
x_{N0} & x_{N1} & x_{N2} & \cdots & x_{NM}\end{bmatrix}
\begin{bmatrix}w_{0} \\w_{1} \\w_{2} \\\vdots \\w_{M}\end{bmatrix}
= {\bf X}{\bf w}
$$
2-3.損失関数と最小二乗法
最小二乗法は正解値(データ$${y_i}$$)と予測値(モデルの計算結果$${\hat{y_i}}$$)の誤差の2乗を最小化する手法です。誤差最小化の指標となる損失関数(評価関数)として一般的に平均二乗誤差(MSE:Mean Squared Error)が使用されます。
$$
MSE=\sum_{i=1}^{n}(y_i - \hat{y_i})^2
$$
2-4.正則化
正則化(regularization)は、機械学習においてモデルの過剰適合を防ぐためにモデルの複雑さにペナルティを課す手法のことです。正則化を行うことにより、モデルの汎化性能が向上し、未知のデータに対してより良い予測を行うことができます。
具体的には損失関数に正則化項を追加することで、正則化項がモデルのパラメータの大きさにペナルティを与えてモデルの複雑さを制御します。
後述しますが、L1正則化(Lasso正則化)はL1ノルムを用いた正則化、L2正則化(Ridge正則化)は、L2ノルムを用いた正則化のことです。
$$
\text{Lasso正則化: } \lambda \sum_{j=1}^n |w_j|
$$
$$
\text{Ridge正則化: } \lambda \sum_{j=1}^n w_j^2
$$
$${λ}$$または$${\alpha}$$:正則化の強度、$${w_j}$$:回帰係数
2-5.中心化(centering)
中心化 (centering) とはデータの平均値が 0 になるように全てのデータを平行移動する処理です。中心化を行うと線形モデルは原点を通るようになるため数値解の計算時にバイアス項が不要になりパラメータを削減できます。
$$
\begin{aligned}
\bf x_{center} &= \bf x - \bar{x}
\\ \bf y_{center} &= \bf y - \bar{y}
\end{aligned}
$$
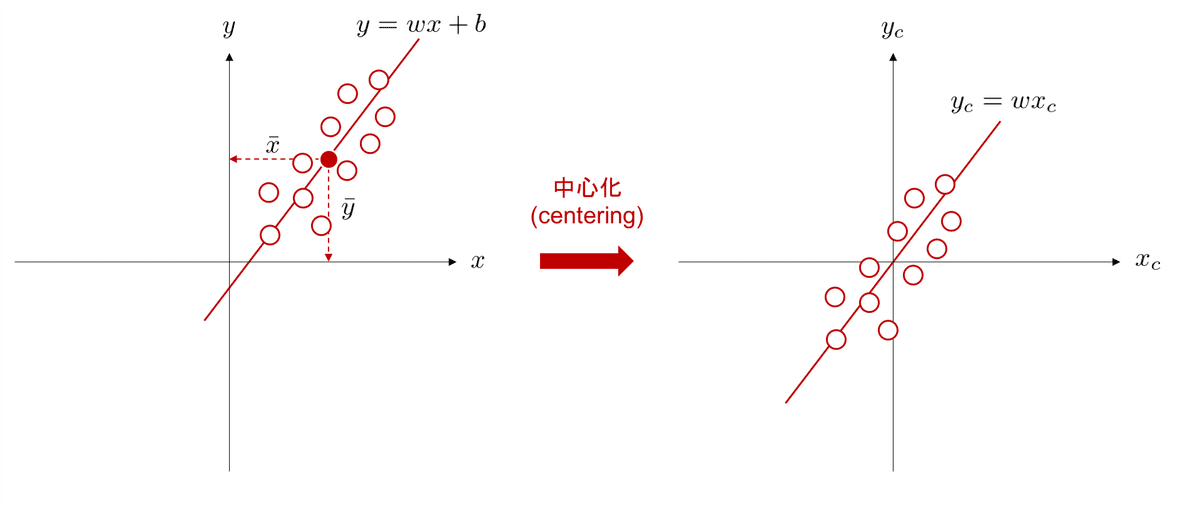
中心化して重み(単回帰なら傾き$${a}$$)$${\bf w}$$を算出後に、中心化前のデータを用いて推論したい場合、バイアス(単回帰なら切片$${b}$$)は$${w_0=\bar{y}-\bf w^T\bar{x}}$$となります。
$$
\begin{aligned}
y_{center} &= wx_{center} \\
y - \bar{y} &= w(x - \bar{x}) \\
\Rightarrow y &= w(x - \bar{x}) + \bar{y} \\
&=wx + (\bar{y}-w\bar{x})
\\ &= wx + w_0
\end{aligned}
$$
リッジ回帰では解析解を算出する際に中心化が重要となります。
3.リッジ・ラッソ回帰の概要
リッジ・ラッソ回帰の説明では「正則項が・・、等高線図より・・・」とありますが、まずは特徴を理解します。リッジ回帰・ラッソ回帰のメリットは「データに過剰に適合しないように重みを調整する項を加える」ことです。これの意味を考えてみます。
3-1.線形モデルにおけるデータの影響
単回帰・重回帰モデルでは下記を含むデータに対して、データの影響を大きく受けます。
外れ値:他のデータの傾向とは明らかに異なる値を持つ値。一般的に四分位数の±1.5倍の値を外れ値として取り扱います。
ノイズ:データに含まれる誤差や不確実性
参考として、ばらつきはデータの母集団に依存しますがノイズは母集団とは独立な事象のため別の概念となります。
例として母集団が正規分布に従う場合、ばらつきは標準偏差に依存しますがノイズは抽出条件や測定方法などに依存します。
多重共線性(Multicollinearity):多変量解析(重回帰分析など)において、いくつかの説明変数間で線形関係(強い相関関係)が複数ある
データによる影響の例として、少ないデータ数で1点だけ過剰な外れ値を追加しました(※正則化項はデータが多く複雑な方が効果が出ますが、この説明ではイメージを理解するために少ないデータを使用しています)。
下図の通り1点加えただけで相関が逆転しており決定係数$${R^2}$$も大きく低下しました。これは線形回帰モデルが外れ値に引き寄せられて過剰に適合していると判断できます。
$$
Data_{外れ値無し}=\begin{bmatrix} x & y \\ 1.0 & 1.75 \\ 2.0 & 2.34 \\ 3.0 & 3.38 \\ 4.0 & 4.97 \\ 5.0 & 5.85 \\ \end{bmatrix},
Data_{外れ値あり}=\begin{bmatrix} x & y \\ 0.0 & 10.0 \\ 1.0 & 1.75 \\ 2.0 & 2.34 \\ 3.0 & 3.38 \\ 4.0 & 4.97 \\ 5.0 & 5.85 \\ \end{bmatrix}
$$

一般的な対策として外れ値を除去する前処理がありますが、貴重なデータを削除するのはもったいなく、またこの方法では多重共線性には対応できません。
リッジ回帰・ラッソ回帰では正則化項を追加して(特に多重共線性による)過学習防止します。
3-2.リッジ・ラッソ回帰に解析解はある?
リッジ回帰・ラッソ回帰の機械学習モデルは重回帰と同じになります。
$$
y = w_{1}x_{1} + w_{2}x_{2} + \cdots + w_{M}x_{M} + b=\sum_{m=1}^{M} w_{m} x_{m} + b
$$
重回帰モデルは解析解$${\bf w = (\bf X^T \bf X)^{-1}\bf X^T\bf t}$$を持つため、ふと「解析解がある線形モデルでなぜ過学習防止ができるのか?」と感じました。
理由としてリッジ回帰・ラッソ回帰は重回帰の機械学習モデルではなく、損失関数の方に正則化項を入れて重み$${\bf W}$$を調整することで最適解とは異なる数値を出すためです。
なおリッジ回帰は解析的な解を求めることが出来ますが、ラッソ回帰はL1正則化項が非微分可能であり解析解を求めることが困難のため最適化アルゴリズム(勾配降下法など)を用いて数値的に解を求めます。
3-3.リッジ・ラッソ回帰の使い分け
リッジ回帰とラッソ回帰は共に正則化項によるペナルティーを与えるため思想は近いですが異なる動作をします。実務的には実装は簡単のため両方試行したらよいですが、理論的には別途使い分けの理解が重要です。
【重要な特徴量(説明変数)の数】
一部の特徴量だけが重要な場合はLasso回帰、全体的に重要であれば
Ridge回帰を使用します。
理由としてLasso回帰はパラメータの値が0になることがあります。不要な特徴量の重みが0になることで特徴量エンジニアリングのような効果が期待されるためと理解できます。
逆に特徴量ごとに意味があったり、それらに相関がある場合などはRidge回帰の方がよい性能が出る可能性があります。

4.リッジ回帰(L2正則化):理論編
4-1.リッジ回帰とは
リッジ回帰(Ridge regression)はL2正則化項:$${\lambda \sum_{j=1}^n w_j^2}$$を損失関数に与えることでモデルの重みが過剰に大きな値になることを防ぎ過学習を防止する手法です。
$$
\underset{w}\min \ \lbrace\sum_{i=1}^n \left( y_i - x_i^\top w \right)^2 + \lambda \sum_{j=1}^n w_j^2 \rbrace
$$
4-2.直接解の計算
4-2-1.結論
リッジ回帰の解析解は下記の通りとなります。
$$
\begin{aligned}
{\bf w} &= ({\bf X}^{\rm T}{\bf X}+\alpha I)^{-1}{\bf X}^{\rm T}{\bf t}
\end{aligned}
$$
$$
E_{Ridge}=\sum_{i=1}^{N}(y_i-\hat{y}_i)^2+\frac{1}{2}\lambda\sum_{k=1}^Kw_k^2
$$
4-2-3.最小二乗和にL2ノルム追加
まずはコスト関数(損失関数)を作成します。重回帰ではMSE:$${MSE=\sum_{i=1}^{N}(y_i-\hat{y}_i)^2}$$を使用しました。リッジ回帰ではMSEにL2ノルム$${\frac{\alpha}{2} \sum_{j=1}^p w_j^2}$$を追加します。
$$
\begin{aligned}
J(\mathbf{w}) &=MSE+ L2正則化項
\\&=\frac{1}{2n} \sum_{i=1}^n (\hat y - y_i)^2 + \frac{\alpha}{2} \sum_{j=1}^D w_j^2
\\&= \frac{1}{2n} \sum_{i=1}^n (w x_i + b - y_i)^2 + \frac{\alpha}{2} \sum_{j=1}^D w_j^2
\end{aligned}
$$
$${y_i}$$:ラベル値(元データによる正解値)
$${\hat y}$$:推論値
$${n}$$:データの個数
$${D}$$:特徴量の数
$${\alpha}$$:正則化パラメータ
$${b}$$:バイアス項(※$${b}$$には正則化項は適用されません)
上記式では参考としてバイアス項を記載しましたが「正則化は機械学習モデルの重みが過剰になることを防止する。つまり特定の特徴量に過敏に反応することがないように、大きな重みの値を持つことを避ける」ことが重要です。つまり「特徴量と関係ないバイアス項に正則化は不要」です。
よって中心化によりデータを原点に移動させることで計算時のバイアス項は0とします。重みを算出後は$${b = \bar{y} - \bar{x}w}$$でバイアス項を算出可能です。
中心化した説明変数$${x}$$, 目的変数$${y}$$を使用すると、数式は下記の通りに変換できます。
$$
\begin{aligned}
J(\mathbf{w}) &=\frac{1}{2n} \sum_{i=1}^n (\hat y - y_i)^2 + \frac{\alpha}{2} \sum_{j=1}^D w_j^2
\\&= \frac{1}{2n} \sum_{i=1}^n (w x_i - y_i)^2 + \frac{\alpha}{2} \sum_{j=1}^D w_j^2
\\&= \frac{1}{2n}(\boldsymbol{y} - X\boldsymbol{w})^T (\boldsymbol{y} - X\boldsymbol{w}) + \frac{\alpha}{2}|| \boldsymbol{w} ||_{2}^2
\end{aligned}
$$
4-2-4.wでの偏微分
コスト関数を微分すると下記の通りです。
$$
\begin{aligned}
\frac{\partial J(\mathbf{w})}{\partial \mathbf{w}}
&= \frac{\partial}{\partial \mathbf{w}} \left[ \frac{1}{2n}(\boldsymbol{y} - X\boldsymbol{w})^T (\boldsymbol{y} - X\boldsymbol{w}) + \frac{\alpha}{2}|| \boldsymbol{w} ||_{2}^2 \right]
\\&=\frac{\partial}{\partial \mathbf{w}} \left[\frac{1}{2n}(\boldsymbol{y} - X\boldsymbol{w})^T (\boldsymbol{y} - X\boldsymbol{w}) \right]+ \frac{\partial}{\partial \mathbf{w}} \left[ \frac{\alpha}{2}|| \boldsymbol{w} ||_{2}^2 \right]
\\&=-X^T (\boldsymbol{y} - X \boldsymbol{w})+ \alpha \boldsymbol{w}
\\&=-X^T \boldsymbol{y} + X^T X \boldsymbol{w} + \alpha \boldsymbol{w}
\\&=-X^T \boldsymbol{y} + (X^T X +\alpha I) \boldsymbol{w}
\end{aligned}
$$
コスト関数を最小化するため$${\frac{\partial J(\mathbf{w})}{\partial \mathbf{w}}=0}$$とすると、$${w}$$の解析解は下記の通りとなります。
$$
\begin{aligned}
\boldsymbol{w} = (X^T X + \alpha I)^{-1} X^T \boldsymbol{y}
\end{aligned}
$$
5.ラッソ回帰(L1正則化):理論編
5-1.ラッソ回帰とは
ラッソ回帰(least absolute shrinkage and selection operator、Lasso、LASSO)はL1正則化項:$${ \alpha \sum_{j=1}^D |w_j|}$$をコスト関数(損失関数)に与えることでモデルの重みが過剰に大きな値になることを防ぎ過学習を防止する手法です。
$$
\begin{aligned}
J(\mathbf{w}) &= \frac{1}{2n} \sum_{i=1}^n (w x_i - y_i)^2 + \alpha \sum_{j=1}^D |w_j|
\\&= \frac{1}{2n}(\boldsymbol{y} - X\boldsymbol{w})^T (\boldsymbol{y} - X\boldsymbol{w}) + \alpha\sum_{j=1}^D |w_j|
\end{aligned}
$$
$${y_i}$$:ラベル値(元データによる正解値)
$${\hat y}$$:推論値
$${n}$$:データの個数
$${D}$$:特徴量の数
$${\alpha}$$:正則化パラメータ
5-2.最適化アルゴリズム
ラッソ回帰の最適化には解析解が存在しないため、勾配降下法や座標降下法などのアルゴリズムを使用します。例として、座標降下法では各特徴量の重み$${w_j}$$について順番に更新していきます。
$$
w_j \leftarrow w_j + \eta \frac{\partial J(\mathbf{w})}{\partial \mathbf{w_j}}
$$
6.Ridgeモデルの実装:スクラッチ編
6-1.Python編
サンプルデータの「Boston housing Dataset」を使用して実装しました。クラスの設計は下記の通りです。
学習時には中心化を実施
推論時は中心化データでなく元データを使用(傾きは中心化前後で不変)
計算結果の過程が見れるようにクラスに変数を持たせた
[IN]
class RidgeRegression:
def __init__(self, alpha: float = 1.0):
self.alpha = alpha
self.weights = None
self.XTX = None
self.XTy = None
self.regularization_term = None
self.intercept_ = None
def fit(self, X: np.ndarray, y: np.ndarray) -> None:
# 中心化
X_centered = X - X.mean(axis=0)
y_centered = y - y.mean()
# 正規方程式の解を求める(X^T X + alpha * I)w = X^T y
self.XTX = X_centered.T @ X_centered
self.regularization_term = self.alpha * np.eye(self.XTX.shape[0])
self.XTy = X_centered.T @ y_centered
self.weights = np.linalg.solve(self.XTX + self.regularization_term, self.XTy)
self.intercept_ = y.mean() - (X.mean(axis=0) @ self.weights)
def predict(self, X: np.ndarray) -> np.ndarray:
return X @ self.weights + self.intercept_
#線形モデル
linear = LinearRegression()
linear.fit(df_2dim[["RM"]], df_2dim["MEDV"])
y_pred = linear.predict(df_2dim[["RM"]])
score_r2_linear = r2_score(df_2dim["MEDV"], y_pred)
print(f"Linear W: {linear.coef_[0]:.3f}, b: {linear.intercept_:.3f}")
#リッジ回帰の実装
ridge_scratch = RidgeRegression(alpha=1.0)
ridge_scratch.fit(df_2dim[["RM"]].to_numpy(), df_2dim["MEDV"].to_numpy())
y_pred_ridge = ridge_scratch.predict(df_2dim[["RM"]].to_numpy())
score_r2_ridge = r2_score(df_2dim["MEDV"], y_pred_ridge)
print(f"Ridge W: {ridge_scratch.weights[0]:.3f}, b: {ridge_scratch.intercept_:.3f}")
# 可視化
fig, ax = plt.subplots(1, 1, figsize=(10, 6), facecolor='w')
sns.scatterplot(x="RM", y="MEDV", data=df_2dim, ax=ax, label="データ")
ax.plot(df_2dim["RM"], y_pred, color="red", label="線形回帰", lw=1.0)
ax.plot(df_2dim["RM"], y_pred_ridge, color="blue", label="リッジ回帰", lw=1.0, ls="-")
ax.text(7.0, 30, f"決定係数(線形回帰):{score_r2:.3f}", fontsize=14, color="red")
ax.text(7.0, 27, f"決定係数(リッジ回帰):{score_r2_ridge:.3f}", fontsize=14, color="blue")
ax.set(xlabel="部屋数[個]", ylabel="住宅価格[k$]")
ax.grid(), ax.legend()
plt.show()[OUT]
Linear W: -0.458, b: 23.925
Ridge W: -0.417, b: 23.675
結果をプリントで出力して各計算結果を確認しました。
[IN]
print(ridge_scratch.XTX) #X^T X
print(ridge_scratch.regularization_term) #αI
print(ridge_scratch.XTX + ridge_scratch.regularization_term) #(X^T X + αI)
print(np.linalg.inv(ridge_scratch.XTX + ridge_scratch.regularization_term)) #(X^T X + αI)^-1
print(ridge_scratch.XTy) #X^T y
print(np.linalg.solve(ridge_scratch.XTX + ridge_scratch.regularization_term, ridge_scratch.XTy))
print(ridge_scratch.weights)
print(ridge_scratch.intercept_)$$
\begin{aligned}
&X^T X =[[10.2441624]]\\
&\alpha I=[[1.]] \\
&(X^T X + \alpha I)=[[11.2441624]]\\
&(X^T X + \alpha I)^{-1}=[[0.08893504]]\\
&X^T \boldsymbol{y}=[-4.68752]\\
&\bf w=(X^T X + \alpha I)^{-1} X^T \boldsymbol{y}=[-0.41688477]\\
&b=\bar y- \bar{x}w=23.67
\end{aligned}
$$
7.モデルの実装:ライブラリ編
ライブラリで実装する場合は複数の機械学習モデルが同じAPIで使用できるScikit-learnを使用していきます。全体フローは下記の通りです。
sklearnの"linear_model"からモジュールをインポート
model = Module()でインスタンス化
model.fit()で学習
model.predict()で推論
損失関数や決定係数などの評価指標を確認
可視化
7-1.リッジ回帰(L2正則化):Scikit-learn/Ridge
sklearnのリッジ回帰は下記の通りです。ポイントとして、解析解は計算可能ですが、反復法を利用する最適化アルゴリズム(ソルバー)を使用する場合は反復回数(max_iter)の指定が必要になります。
[API]
class sklearn.linear_model.Ridge(alpha=1.0, *, fit_intercept=True, copy_X=True,
max_iter=None, tol=0.0001, solver='auto',
positive=False, random_state=None)【sklearnでの損失関数】
$$
||y - Xw||^2_2 + \alpha * ||w||^2_2
$$
【パラメータ】
alpha:L2正則化項に掛ける定数(0以上の浮動小数点数)
alpha=0の場合、目的関数は通常の最小二乗法に相当する
fit_intercept:モデルの切片の有無
copy_X:True->Xがコピーされる、False->Xは上書きされる可能性がある
max_iter:共役勾配法ソルバーの最大反復回数
sparse_cg, lsqr のDefault:scipy.sparse.linalg
sagのDefault:1000
lbfgsのDefault:15000
tol:解の精度(※「svd」と「cholesky」ではtolは影響しない)
solver:最適化のためのアルゴリズム
'auto':データの種類に基づいてソルバーを自動的に選択
'svd':Xの特異値分解を使用してRidge係数を計算(最も安定)
'cholesky':閉形式の解を得るため標準のscipy.linalg.solve関数を使用
'sparse_cg':大規模データに適した反復アルゴリズム。
'lsqr':最速で反復手順を使用する専用の正則化最小二乗ルーチン。
'sag'及び'saga':両方とも反復手順を使用し、大規模なn_samplesおよびn_featuresの場合に他のソルバーよりも高速で動作する
positive:Trueに設定->強制的に係数を正にする(※lbfgsのみ対応)
random_state:solverが'sag'または'saga'の場合にデータをシャッフル
【属性】
coef_:重みベクトル
intercept_:判定関数の独立項
n_iter_:各ターゲットに対する実際の反復回数(Ver.0.17で追加)
sagとlsqrソルバーでのみ利用可能
他のソルバーはNoneを返します
n_features_in_:fit中に見られた特徴量の数(Ver.0.24で追加)
feature_names_in_:fit中に見られた特徴量の名前
Xがすべて文字列である特徴量名を持つ場合にのみ定義されます
実装は”sklearn.linear_model”から実装可能です。
[IN]
[IN]
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge, Lasso
#モデル定義
linear = LinearRegression()
ridge = Ridge(alpha=1.0)
#学習
linear.fit(df_2dim[["RM"]], df_2dim["MEDV"])
ridge.fit(df_2dim[["RM"]], df_2dim["MEDV"])
#推論
y_pred_linear = linear.predict(df_2dim[["RM"]])
y_pred_ridge = ridge.predict(df_2dim[["RM"]])
#決定係数(r2_score)
r2score_linear = r2_score(df_2dim["MEDV"], y_pred_linear)
r2score_ridge = r2_score(df_2dim["MEDV"], y_pred_ridge)
print(f'単回帰の係数 w:{linear.coef_}, b:{linear.intercept_}')
print(f'Ridgeの係数 w:{ridge.coef_}, b:{ridge.intercept_}')
print(f'決定係数 単回帰:{r2score_linear:.3f}, Ridge:{r2score_ridge:.3f}')
# 可視化
labels = ["単回帰", "Ridge"]
scores = [r2score_linear, r2score_ridge]
xs, ys = [df_2dim["RM"], df_2dim["RM"]], [y_pred_linear, y_pred_ridge]
plot_multidata(xs, ys, labels, scores)[OUT]
単回帰の係数 w:[-0.45757963], b:23.92493834342183
Ridgeの係数 w:[-0.41688477], b:23.674591697466074
決定係数 単回帰:0.001, Ridge:0.001
7-2.ラッソ回帰(L1正則化):Scikit-learn/Lasso
sklearnのラッソ回帰は下記の通りです。
[API]
class sklearn.linear_model.Lasso(alpha=1.0, *, fit_intercept=True, precompute=False,
copy_X=True, max_iter=1000, tol=0.0001,
warm_start=False, positive=False,
random_state=None, selection='cyclic')【sklearnでの損失関数】
$$
\frac{1}{ (2 * n_samples)} ||y - Xw||^2_2 + \alpha * ||w||_1
$$
【パラメータ】
alpha:L1項に掛ける定数で正則化の強度を制御(0以上の浮動小数点数)
alpha=0の場合、目的関数は通常の最小二乗法に相当する
Lassoオブジェクトではalpha=0の使用は推奨されない
fit_intercept:モデルの切片の有無
precompute:事前計算されたグラム行列を使用有無(計算を高速化)
グラム行列は引数として渡すことも可能
疎入力の場合このオプションは常にFalseに設定され疎性を保持する。
copy_X:True->Xがコピーされる、False->Xは上書きされる可能性がある
max_iter:最大反復回数。
tol:最適化の許容誤差。更新がtolより小さい場合、最適化コードは双対ギャップの最適性をチェックし、tolより小さくなるまで続ける。
warm_start:Trueで前回のfit呼び出しの解を初期化として再利用する
positive:Trueに設定->強制的に係数を正にする
random_state:乱数値のシード
selectionが'random'の場合に使用
複数の関数呼び出しで再現可能な出力を得るにはintを渡す。
selection:'random'に設定すると、デフォルトで特徴を順次ループする代わりに、各反復でランダムな係数が更新される。これにより、特にtolが1e-4より大きい場合、収束が大幅に高速化されることが多い。
【属性】
coef_:パラメータベクトル(コスト関数式の$${w}$$)
dual_gap_:与えられたパラメータ$${\alpha}$$に対して、最適化の最後に得られる双対ギャップ。yの各観測と同じ形状。
sparse_coef_:fitされたcoef_の疎表現
intercept_:判定関数の独立項
n_iter_:指定許容誤差に到達までの座標降下ソルバーが実行した反復回数
n_features_in_:fit中に見られた特徴量の数(Ver.0.24で追加)
feature_names_in_:fit中に見られた特徴量の名前。Xがすべて文字列である特徴量名を持つ場合にのみ定義されます
実装は”sklearn.linear_model”から実装可能です。
[IN]
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge, Lasso
#モデル定義
linear = LinearRegression()
lasso = Lasso(alpha=1.0)
#学習
linear.fit(df_2dim[["RM"]], df_2dim["MEDV"])
lasso.fit(df_2dim[["RM"]], df_2dim["MEDV"])
#推論
y_pred_linear = linear.predict(df_2dim[["RM"]])
y_pred_lasso = lasso.predict(df_2dim[["RM"]])
#決定係数(r2_score)
r2score_linear = r2_score(df_2dim["MEDV"], y_pred_linear)
r2score_lasso = r2_score(df_2dim["MEDV"], y_pred_lasso)
print(f'単回帰の係数 w:{linear.coef_}, b:{linear.intercept_}')
print(f'lassoの係数 w:{lasso.coef_}, b:{lasso.intercept_}')
print(f'決定係数 単回帰:{r2score_linear:.3f}, lasso:{r2score_lasso:.3f}')
# 可視化
labels = ["単回帰", "lasso"]
scores = [r2score_linear, r2score_lasso]
xs, ys = [df_2dim["RM"], df_2dim["RM"]], [y_pred_linear, y_pred_lasso]
plot_multidata(xs, ys, labels, scores)[OUT]
単回帰の係数 w:[-0.45757963], b:23.92493834342183
lassoの係数 w:[-0.], b:21.110000000000003
決定係数 単回帰:0.001, lasso:0.000
参考資料
あとがき
次はベイズ線形回帰とガウス過程回帰
