ポートフォリオ効果(分散投資)の説明
ポートフォリオ効果
リターンを減らさずにリスクを減らす素晴らしき金融発見
はじめに
投資においてリターンを減らさずにリスクを減らすのは原則的には不可能であると考えた方が良い。
希にそのような歪みが現れることがあるが、市場はその歪みを瞬く間に修正してしまう。我々個人投資家がそのような奇跡を享受できる可能性よりも、詐欺に遭う可能性の方が圧倒的に高いだろうから、下手な欲は出さずに諦めた方が良い。
だがしかし、先に述べた「原則的に」という言葉は逆説的に「例外的に」が存在することを示唆するわけだが、今回の言葉にもそれが当てはまる。
今回はその例外的な「ポートフォリオ効果」について説明する。
ポートフォリオ効果とは
ポートフォリオ効果は1952年にハリー・マーコウィッツが書いた「ポートフォリオ選択論」にて示したものだ。
私はこの本自体は読んだことはない。
現代ポートフォリオ理論で用いられる数学は難解で近づきがたいものがある。学術誌は数式で満ち溢れており、多くの学者がその取扱いに忙殺されている。
このように難解な数式が記述されとにかく難しいという評判は聞いている。だが私と、そして読者にとって幸いなことにその理解自体には難しい数式を考える必要は無い。
すなわちポートフォリオ効果とは、「低い相関係数を持つ複数の金融商品に分散投資するだけで、それぞれのリスクは相殺し合うのに対して、リターンは平均化される効果」のことだ。
なお今回は計算結果のみを記述している。途中計算が気になる方は、ご自身で調べてほしい。
ちなみに私なら標準偏差はモーニングスターなどから。相関係数は証券会社、政府機関が発表した物を使っている。
さてそのポートフォリオ効果をもう少し簡単に説明する。
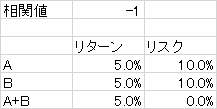
ここにAとBの株式がある。
このAとBの株は両方ともリターン5%リスク10%である。
そして大事なことはこの二つの値動きは正反対の動き、すなわち相関係数が-1であることだ。
例えばAが10%値上がりすればBは10%値下がりする。Bが上がればその逆になる。
よって、二つの株を同量保有しているとあわせた値動きは0になる。
一方でリターンは二つの平均となるから5%のままだ。
結果、AとBを同量保有する投資家の資産は年率5%から全くぶれることのない、すなわちリスクのない素晴らしいポートフォリオとなる。
誰だって同じリターンならよりリスクが低い方を選ぶだろう。
更にリスクが全く無いと言うことがどれくらい素晴らしいかと言えば、金利年率5%未満ならどれほど借金しても資産が増えるということであり、貴方の資産を同リターンでリスクあるものよりも早く大きく成長させることが出来るのだ。もちろん例え話であることに留意して借金は軽率にしないようにして欲しい。
このような夢のためには相関係数-1が必要だが残念ながらそのようなものは現実には存在しない。
だが失望するのは早計だ。ポートフォリオ効果は十分現実で享受することが出来る実用的なものだ。
では次に相関係数が0.5である場合を考えてみよう。0.5ということはAが値上がりすればBもだいたい値上がりすると言うことだ。少し注意して欲しいが、相関係数が0.5であることは常にAの動きの半分Bが動くというほど単純なものではない。
AとBの株は両方とも先ほどと同じリターン5%リスク10%であるとする。
するとリターンは5%、リスクは7.9%となる。

今度は相関係数0.9で同じAとBの場合でも、リターンは5%リスクは9.7%となる。

このことから相関係数が1、すなわち全く同じ値動きでなければどんな株でも組み合わせればリスクが減ることが分かる。
ポートフォリオ効果の素晴らしい点は、相関係数-1等という伝説の存在を探さずに、0.8や0.9でもある程度のリスク軽減を実現できる点にある。
そして株式市場において相関係数0.8程度でも大量の銘柄を見つけることが出来るだろう。
まとめ
ポートフォリオ効果はよく言われる分散投資の利点を数学的に説明したものになる。
「卵は一つのカゴに盛るな」とはよく言われることわざだが、入れた場合と入れない場合はどれほど違うのか? どんなカゴにいくつ分ければ良いのか? といった疑問にポートフォリオ効果は答えてくれる。
一つのカゴ、すなわち相関係数が高いということは相対的に高いリスクを負っているということであり、またそのカゴ同士の相関係数が低ければ低いほど良いのだ。
逆に相関係数が高いカゴに幾つ分けたところで意味は無い、ということも分かる。
例えばJALとANA(2社とも似た航空会社)に投資することは分散投資ではないし、日本株式と日本REITも分散投資としては弱い。
このように相関係数が低い、すなわちよく分散されたポートフォリオはそうでないものに比べてリスクが明確に低いこと、すなわちより優れたポートフォリオであることを示している。
是非この仕組みを有効活用して、金融資産の育成に励んで欲しいと思う。
蛇足
なお、ポートフォリオ効果を根拠に、私は株式の分散投資を推奨してはいるが初心者が株式以外の金融商品、債券やREITなどにまで投資を広げることは推奨してはいない。その理由は困難な売買判断のいらないバイアンドホールド(買ってただ耐えること)を初心者に勧めているからだ。そしてバイアンドホールドならば、債券など他の金融資産を組み込むより株式を100年持ち続けるのが最もリターンがあると考えてる。
初心者と株式に手間をかけたくない方は是非分散された世界株式投資信託にじっくり投資して欲しい。
投資の世界はことわざに満ちている。だがことわざが本当か疑うことを忘れてはならない。
ことわざの中には間違っている物や、間違っているかどうかさえも分からないものがある。
先人達はことわざを科学的に検証する環境が無かったのだから仕方ない。だが我々は彼らよりも遙かに恵まれた環境にいる。折角の恵まれた環境を是非活用してほしい。
この記事が気に入ったらサポートをしてみませんか?
