
基礎問題精講数学2B 79大小比較(Ⅱ)解説
(1) Pのとりうる値の範囲を求めよ. ※ [] は底として扱う
〇問いから a と b の大小関係が分かるので無理やりPにもっていく
与えられた情報から求めたいものに繋げる。
1<a<b の全体に底がbの対数をとることで
log[b]1<log[b]a<log[b]b
log[b]1 は真数が1なので0, log[b]b は底と真数が一致するので1,
よって上の式は
0<log[b]a<1.
log[b]a はPなので
0<P<1. (答え)
(2) Q, R を P( log[b]a ) で表せ.
Q=log[b](log[b]a)=log[b]P. (答え)
R=(log[b]a)^2=P^2. (答え)
(3) P,Q,R を小さい順に並べよ.
(1)で 0<P<1 だとわかっています.
ここでPについて確認すると, Pは0より大きくて1より小さい数なので,
分数形か小数形であると置き換えて考えられる.
分数や小数は2乗すると元の数より小さくなるので
Pの2乗であるRはPより小さいことが言える
⇒0<R<P.
〇次にQ(log[b]P)についてグラフを書いて想像していく.
グラフを書くので底の大きさを確認
⇒問題文より底bは1より大きいことから右上に曲線を描く.
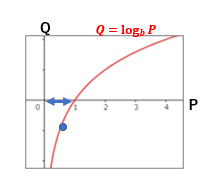
今回(1)の(0<P<1) よりこの曲線の中で真数であるPは0から1の間しか動けない. (※青の矢印の範囲)
この範囲内ではずっと負の値を示すので
Q<0. とわかる.
0<R<P と Q<0 を合わせて
Q<R<Pとなり並べると
Q、R、P . (答え)
演習問題、解き方、ポイントが確認できます⇒
基礎問題精講 数学1A
https://www.amazon.co.jp/dp/4010347066/
基礎問題精講 数学2B
https://www.amazon.co.jp/dp/4010347074/
