基礎問題精講数学1A 90.不定方程式

(1)

例えばｘ＝２、ｙ＝１とすると
２ｘー３ｙ＝２・２ー３・１＝７   となって成立。

よって➀をみたす（ｘ、ｙ）の一組は（２，１）。（答え）
ほかにも（５，１）や（ー１、ー３）などがある。

(２) 

２ｘー３ｙ＝７･･･➀　　２αー３β＝７･･･②
➀ー➁より、　←この作業はセンター。共通テストでも頻出
　　２ｘー３ｙ＝７　　　　　
ー）２ αー３ β ＝７
【２ｘー２α  ー３ｙー（ー３β）＝７－７】  ←※【】内途中計算
【２（ｘ－α）ー３（ｙ－β）＝０】

∴２(ｘ－α)ー３(ｙーβ)＝０･･･☆

☆を移項して整理すると
２(ｘ－α)＝３(ｙーβ)･･･☆´
☆´について考えていく。

右辺）係数に３が付いているので３の倍数です。
さらに「＝」で結ばれているので  左辺も  ３の倍数です。
〇左辺である２(ｘ－α)が３の倍数になるには？

２(ｘ－α)という式に注目して
２×（ｘ－α）。
２×「何か」が３の倍数になるには「何か」が３の倍数だと成立。
よって、
(ｘ－α)は３の倍数

左辺）係数に２が付いているので２の倍数です。
さらに「＝」で結ばれているので右辺も２の倍数です。
〇右辺である３(ｙーβ)が２の倍数になるには？

３(ｙーβ)という式に注目して
３×（ｙ－β）。
３×「何か」が２の倍数になるには「何か」が２の倍数だと成立。
よって、
（ｙ－β）は２の倍数

(３)

(２)より、（ｘ－α）が３の倍数。（ｙーβ）が２の倍数であることをｎを用いて表現する。
（ｘ－α）＝３ｎ、 （ｙ－β）＝２ｎ（ｎは整数）。
(２)で(１)で求めた組を（α、β）とおいているので直して

ｘ－２＝３ｎ　　　　　⇒ 　ｘ＝３ｎ＋２
ｙー（ー１）＝２ｎ　　⇒　ｙ＝２ｎー１

➀をみたす(ｘ、ｙ)をすべて求められた
(ｘ、ｙ)＝(３ｎ＋２、２ｎー１)　（ｎは整数）　　（答え）
　　　　　↑ｎにいろいろな整数を入れると➀をみたす組を出せる

(４)

（３）でｘ（３ｎ＋２）とｙ（２ｎー１）をｎを用いて求めているので代入して

グラフ作成↓

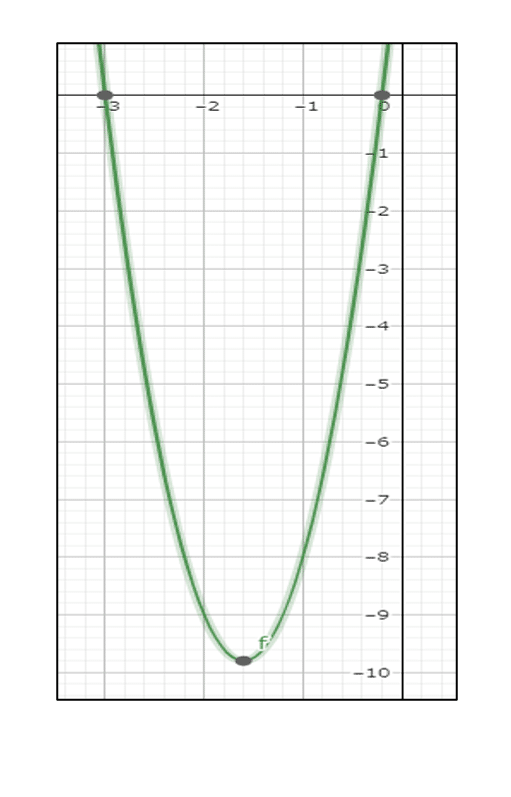
下に凸の２次関数なので最小値は頂点の座標で取りたいが
(３)でｎは整数と決めたので、
頂点のｎ＝ー８/５の時に最小値にとれません。

ｎ＝ー８/５＝ー１.６であるからー１よりー２の方が頂点に近いです。
よって、
ｎ＝ー２のとき

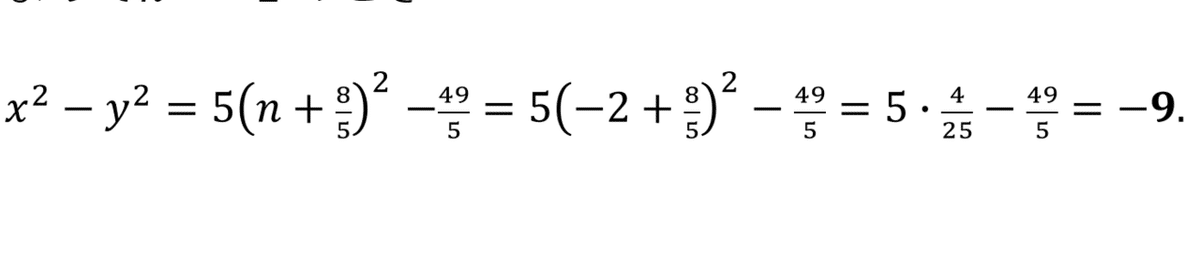
最小値をとるときのｘとｙの値も求めなければいけないので
(ｘ、ｙ)＝(３ｎ＋２、２ｎー１)にｎ＝ー２を代入して
(ｘ、ｙ)＝(３（ー２）＋２、２（ー２）ー１)
　　　  ＝(ー４、ー５）

∴（ｘ、ｙ）＝（ー４、ー５）のとき最小値ー９をとる。（答え）

演習問題、解き方、ポイントが確認できます⇒

基礎問題精講　数学１A
https://www.amazon.co.jp/dp/4010347066/
基礎問題精講　数学２B
https://www.amazon.co.jp/dp/4010347074/