
基礎問題精講数学1A93.整数問題(Ⅰ)
(1)
pqーpー2q+2 をpについて整理していきます。
pqーpー2q+2=p(q-1)ー2q+2 2でくくって
=p(q-1)ー2(q-1)
=(p-2)(q-1) (答え)
pqーpー2q+2 をqについて整理していきます。
pqーpー2q+2=q(p-2)ーp+2
=q(p-2)ー(p-2)
=(p-2)(q-1) (答え)
(2)
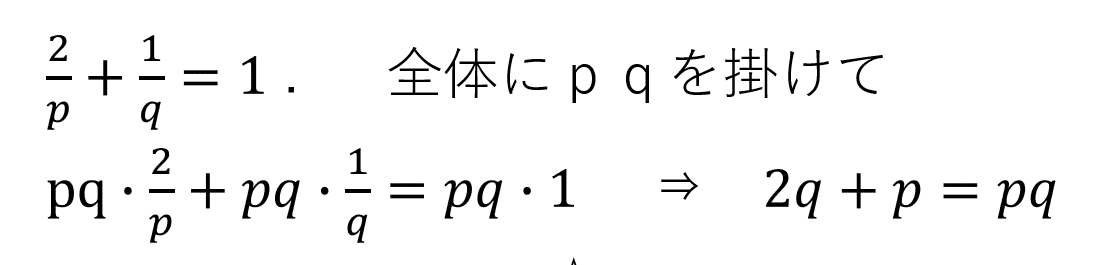
右辺に移項して、
pqーpー2q=0.
全体に2足すと
pqーp-2q+2=2.
左辺に注目すると(1)で因数分解した形なので
(p-2)(q-1)=2 となる.
よってこの方程式の解を求めます。
準備)
・問題文からpとqは整数だからp-2とq-1も整数です。
(整数-整数=整数のため)
・2/p+1/q=1もついて確認すると、pとqは分母だから0以外の整数であることもわかります。 (p≠0、q≠0)
※分母が0だと分数として成り立たない
p≠0より、全体から2引いて(p-2)に無理やり持っていくと
p-2≠ー2となる。
q≠0より、全体から1引いて(q-1)に無理やり持っていくと
q-1≠ー1となる。
(p-2)(q-1)=2を解いていく。
掛けて2になるペアは
(p-2、q-1)=(2,1)(1,2)(ー1,ー2).
3通り計算して
➀ p-2=2、q-1=1
∴p=4、q=2
➁ p-2=1、q-1=2
∴p=3、q=3
③ p-2=ー1、q-1=ー2
∴p=1、q=ー1
よって
(p、q)=(4,2)(3,3)(1,ー1) (答え)
演習問題、解き方、ポイントが確認できます⇒
基礎問題精講 数学1A
https://www.amazon.co.jp/dp/4010347066/
基礎問題精講 数学2B
https://www.amazon.co.jp/dp/4010347074/
この記事が気に入ったらサポートをしてみませんか?
