
基礎問題精講数学2B 115.等比数列(Ⅱ)
(解答1初項を固定する)
初項を a, 公比を r とおくと、
「初項から第10項までの和が3」は
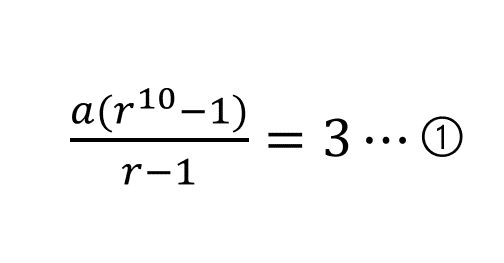
「初項から第30項までの和」は

と表せる。
求めたい第31項から60項までの和をSとおきます。
初項から第60項までの和 = 初項から第30項までの和+第31項から第60項までの和なので式で表して
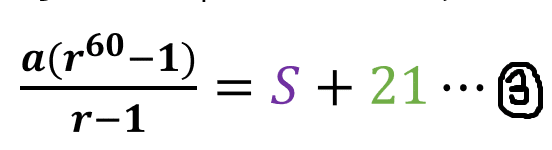
➁÷➀をすると、

〇r^10 +3について、
公比rが負の数でも10乗したら正の数になる
ex. (-2)^10=1024>0
これより、r^10(>0)+3(>0)は絶対に0よりは大きい
だから r^10+3が0になることはないので解なし.


↓ (r^10)^6=2^6=64.

(解答2 初項を変えていく)
「初項から第10項までの和が3」 というのは
初項a, 公比r とおくと
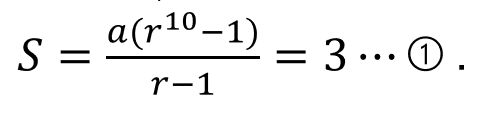
「第11項から第30項までの和が18」 というのは
第11項(ar^10)を初項と考えて公比rとおくと、
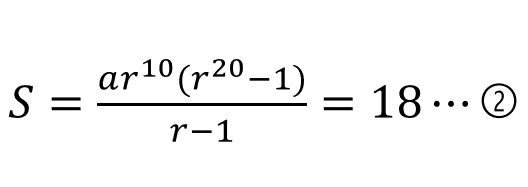
➁÷➀より


演習問題、解き方、ポイントが確認できます⇒
基礎問題精講 数学1A
https://www.amazon.co.jp/dp/4010347066/
基礎問題精講 数学2B
https://www.amazon.co.jp/dp/4010347074/
