【AtCoder】ABCの過去問、緑まで全部埋めてみた!【Beginner Contest】
Accepted! 現在緑コーダーの霧しゃまです。
去る2023年3月18日、登録から136日掛けて、その時点での「難易度が緑色ランク以下の問題」を完走しました!
ということで、今回は完走した感想と、全部埋めてみて得られた知見の共有です!
忙しい人向けのまとめ(産業でおk)
・「昔の問題のほうが簡単」は本当!
・『鉄則本』があれば、ライブラリの面ではほとんどカバーできる!
・同色以下の問題はレートの安定には寄与するけど、レートを上げたければ上の難易度の問題を解こう!
全部で何問あるの?
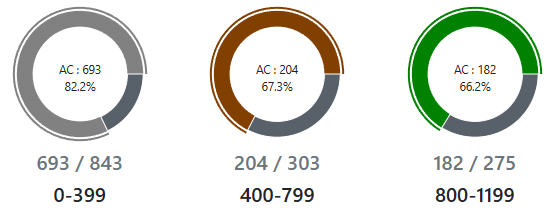
ABC293まで(2023年3月18日時点)で、ABC-Likeなコンテストも含めると、灰色 693 問、茶色 204 問、緑色 182 問あるようです。
今回の記事では、難易度のついていないA問題またはB問題の 13 問(以下、無色とします)も加えた 1092 問について紹介していきたいと思います。
完走した感想
完走というか、コンテストが開催される限り新たな問題は増え続けるのですが、そこは一旦置いといて。
中の人はABC 3 完程度の実力からAtCoderを開始したので、灰色ランクの問題は概ね解くことができる状態でした。
自分の実力より大幅に簡単な問題を解くことを「虚無埋め」と言ったりします。それでも簡単なほうから埋めているのは、次のような理由があります。
問題文の表現や、問題の傾向に慣れるため
ライブラリ等を整備し、コーディングスタイルを確立するため
知的瞬発力を鍛え、早解き力を向上させるため
基礎的な部分の取りこぼしをなくすため
まあ実際、ABCのA問題(ほぼ灰色)にそういう効果があるのかは微妙ですが、割とB問題(9割以上灰色)辺りでは不定形な貪欲法シミュレーションや全探索などをゴリゴリと実装させる問題も出るので、高度なアルゴリズムばかりやっていても本番で思わぬロスをすることがあります。
霧しゃまは1月28日に入緑しましたが、それまでに解いたのが
無色 11 問 灰色 355 問 茶色 112 問 緑色 93 問 合計 571 問
なので、入緑以降に解いた問題は
無色 2 問 灰色 338 問、茶色 92 問、緑色 89 問 合計 521 問
になります。この圧倒的に多い灰色問題を「せっかくなら全部解きたい」と思ってしまったために、かなりの時間を費やすことになりました。
だいたい茶色や緑色を 1 問解く間に、灰色は 3~5 問くらい解けますが、それでもこれだけの問題数はなかなか終わりませんでした。
もう、レートも1000を超えていて、入水に向けた準備をする時期に入っているので、これらの問題に時間を掛けている場合ではなくなってきています(実際、最近ちょっとレートの伸びが鈍化しています)。
ということで、この 3 月中に埋めきると決心し、無事に達成したのでした。
入緑から約 50 日間でだいたい 1 日 10 問のペースでしたが、空いた時間のすべてを競プロに捧げるような生活になってしまったので、今後は少しペースを落としたいと思っています。並行してABCの水色に毎日取り組んでいるので、それに加えてARCの緑以下の問題にも手を付けていく予定です。あとは、典型90やEDPCなんかも……やりたいことが多すぎる!
結局、どこから埋めるのが良い?
ここからは、AtCoderの初心者向けの記事で必ず話題になるいくつかのテーマについて触れていきたいと思います。まずは「どこから埋めるか」です。
霧しゃまはABC042から緑以下の問題を拾いつつ上がっていきましたが、このスタイルで良かったと感じたのは「難易度曲線がちょうどよい」点です。
序盤は最近に比べて単純な問題が多いので、「競プロ自体に慣れる」目的の練習ができる
ABC126あたりから名のあるアルゴリズムやデータ構造の問題、クエリ問題などが増えてくるので、学んだことを活かしやすい(ここで『鉄則本』と併用すると相乗効果あり)
ABC212あたりから手応えのある問題が増えてくるので、演習の強度が落ちにくい
全部埋めるのが面倒だったり時間がなかったりする場合は、最新から下がっていくほうが解き甲斐のある問題に当たりやすいので良いかもしれません。あるいは、ランダムにやりましょう。バーチャルコンテストも良いです。
本当にプログラミング自体を始めたばかりの人は、A問題をABC150あたりから埋めていきましょう。あまり新しいとforなども要求しますし、あまり古いと解説が充実していなかったりします(A問題でforはABC272から本格的に出ていますが、それ以前でも何度かあった印象です)。
ちなみにABC041以前のいわゆる「試験管diff」と呼ばれる問題は、やらなくてもよいという感じです。ただ、いくつか有用なテクニックを抽出した問題がある(ABC007C - 幅優先探索 など)ので、余裕があれば覗いてみましょう。霧しゃまは年末年始の時間がある時期につまんでいきました。
どんな知識が必要なの?
始めたての初心者にとって最大の課題は、「知識がないために問題が解けない」ことです。まあこれは水色以上でもずっとあるのですが、緑色以下の問題では何か典型的な考えそのままの問題も多いので、「知らなかったから解けなかった」ということがよくあります。
ということで、緑色以下で使ったことのあるテクニック類をまとめます。
だいたいジャンル別にずらーーーっと並べていきます。
言語はC++前提ですが、Pythonでもだいたい同じだと思います。
概ね難易度順なので、この順番にやると良いかもしれません。
一部の特徴的な問題については番号を書いておきます。
ネタバレになるのでご注意ください!
割り算の切り捨て・切り上げに関する操作
AND条件やOR条件、短絡評価などの条件関連
閉区間や開区間の使い分け、区間のANDやOR
演算子の優先順位を考慮したコーディング
オーバーフローの回避(制約に合わせたデータ型を用意する)
実数演算(割り算や平方根)の回避、誤差対策
基数変換(2進数~16進数、昔のExcelの列ID式26進数)
再帰関数(配列を参照渡しする、グローバル変数を使う、など)
最大公約数や最小公倍数の計算(ユークリッドの互除法)
素数判定およびエラトステネスの篩(ABC170台に結構多い)
素因数分解(試し割りの範囲の見極めがかなり重要)
ビット演算、特にXORの性質(ABC171Eがおすすめ)
基本動作です。あらゆる問題で部分要素として出現したりします。最大公約数や最小公倍数、素数判定あたりは昔のほうがよく出ていた印象です。
あと、数学という意味では高校くらいまでの数え上げがわかれば概ね大丈夫です。ただ、「ある事象が起こるまでの試行回数の期待値」はかなり重要なので、ABC078Cで早いうちに習得しましょう。
確率の写像十二相にしか出てこない範囲は、緑以下では必要ありません。「形式的べき級数」や「畳み込み」も不要ですが、簡単な問題で練習するという意味では良いかもしれません。
Σの式変形は結構よく出てきます。やりながら覚えましょう。
行列(線形代数)関連はほぼ全く出ませんが、Monge性の判定問題があります(ABC224B)。
forによる配列やグリッド等の全探索、範囲for[拡張for、foreach]
ビット全探索(ビットDPはまだ見たことがない)
文字型の操作(大文字小文字判定、数値型との相互変換など)
文字列の操作(回文判定、部分文字列、正規表現、フォーマットなど)
ソートの利用(ソートを利用すべき場面の見極め)
setやmapの利用
stack、queue、deque、priority_queueの使い分け
lower_boundやupper_boundなど、イテレータ関連の機能
next_permutationによる順列全列挙と、iotaによる順列生成
バケットソートやイベントソート(制約に応じた使い分け)
multiset(かなり仕様に癖がある、代替があるならそれで)
セグメント木(そのもの問題はABC185Fだけ?)
クエリ問題の基本的捌き方(O(N)かかる操作は実際にしない、など)
インタラクティブ問題の実装(ABC244CとABC269Eの 2 問だけ)
データ構造系、実装系です。文字列では、RollingHashは必須ではありませんでした。あと、Z-algorithmやSuffix Arrayなども使ったことがありません。
データ構造に対するクエリ問題も割と頻繁に見ますが、だいたいO(N)の操作が混ざっているので、それを別の方法で表現できればOKです。その他の区間系クエリなどの問題は、ほとんどが累積和などによる前計算です。
セグメント木は、緑以下だとほとんど使いません。Sparse TableやBIT(フェニック木)などとともに、別解に出てくるくらいです。
multisetの代替としては、ウェーブレット行列があると後々役立つかもしれません。様々な機能を盛り込めるので時間を掛けて作りたいところです。
平衡二分探索木の類も緑以下では不要です。
ユークリッド距離、マンハッタン距離、チェビシェフ距離(ABC180B)
マンハッタン距離問題の45度回転典型(ABC178Eで練習できる)
三角関数と幾何(度数法と弧度法の相互変換や、逆三角関数が頻出)
幾何です。三角関数の仕様には慣れておく必要があります。例えば、逆三角関数で返される角度が時計回りなのか、反時計回りなのか、など。ベクトルの演算も若干使った覚えがあります。回転行列もあります。
他には、円の位置関係の判定や、四角形の凸性判定みたいな問題があります。螺旋本16章にある幾何ライブラリの範囲では、凸包は出ません。他は使いどころがあるような気がします。
累積和およびいもす法(あらゆるところで非常によく使う)
二分探索(整数でも実数でも出る、「答えで二分探索」は出ない?)
動的計画法(EDPCのHくらいまで? LISや区間DP、桁DPなどは出ない)
メモ化再帰(ABC275Dが入門問題、DPで代替できる)
繰り返し二乗法およびダブリング
modの四則演算(拡張ユークリッドの互除法で逆元を求める問題もある)
mod二項係数と、パスカルの三角形型DPによる二項係数
競プロらしい操作です。累積和やいもす法は最優先で習得しましょう。DPはABC230あたりから頻繁に出てきます。慣れないうちは嘘貪欲に陥りがちですが、DPに慣れると使いどころが徐々にわかるようになると思います。
二項係数については、modを使う場合と使わない場合の両方が必要です。階乗を掛けたり割ったりする公式だとオーバーフローの回避が難しいので、パスカルの三角形の要領で下から求めるのが良いでしょう。具体的には、$${\binom{66}{33}}$$くらいが64bitで収まる限界で、たまに狙われます。ABC254Bなどをやって、ライブラリとして作っておきましょう。
逆元は、O(N)で前計算するアルゴリズムがmod二項係数とセットで便利ですが、局所的に一つだけ必要になることがたまにあるので、拡張ユークリッドの互除法も仕入れておきましょう。
グラフの用語(単純、有向無向、木の定義など)
DFSあるいはBFSによるグラフやグリッドの全探索、重みなし最短経路
DFSによる構築問題(辞書順関連や、単調増加数列関連)
Union-Findによる連結判定、連結成分の個数、無向閉路の検出
橋および関節点(ABC075Cが入門問題、稀に見る)
クラスカル法(ABC218Eが入門問題)
ワーシャルフロイド法(ABC208Dが入門問題、結構よく使う)
ダイクストラ法(重み付きグラフ問題が少ないのであまり使わない)
トポロジカルソート(あまり使わないが必要になるときは必ず来る)
強連結成分分解(使わなくても良い)
最小共通祖先(使わなくても良い)
グラフです。木の直径とか、オイラーツアーとか最大流とか、目に入るものはいろいろありますが、緑以下はDFSやBFSができれば解ける問題ばかりです。それにしても様々な類型があるので、何か基本的なテンプレートを用意して、都度調整するようにすると効率が良いと思います。
再帰DFSの実装に慣れると、解ける問題の幅がかなり広がります。構築問題などグラフ以外の問題で使うこともあります。
Union-Findも、適当なライブラリを拾って意味さえ理解してしまえば、応用範囲がとても広いです(しかも、最近大流行しているようです)。
解いた問題、どう管理する?
霧しゃまは復習というものが好きではありません。解いたその場で印象付けて、折に触れて思い出せるようにしておくタイプです。
具体的には、解いたそれぞれの問題について、ノート(Simplenoteというアプリを使っています)に内容の要約と、考察した内容や解いた感想、解説を読んで学んだことをまとめて書いておきます。こんな感じです。

これだけだと検索性が悪いので、定期的にジャンルごとのまとめノートを作って、自分なりに「典型」を整理しています。これは本番で「連想力」を発揮するための準備です。一見して解き方がわからないときは、過去に似たような問題を解くために使った手法をあれこれ試してみます。そこで、似たような問題をどれだけ思い出せるか、見つけられるかがポイントになるわけです。ごく稀に、過去問題そのままの問題も出るようなので……。
解説ACをした問題は、ちゃんとそう書いておきます。すべての問題で時間を計っているので、だいたい一時間やって無理そうだったら解説を見るという「足切りタイム」を設けています。
鉄則本との対応について
『競技プログラミングの鉄則』という競プロ攻略本があります。
この本にはここまで見てきたようなテクニックの大部分が紹介されているので、とりあえずやっておくには最適です。
ただ、数学的な問題のうち、幾何や確率・期待値系がほとんど載っていないので(mod関連や数え上げも多くない)、その辺りが苦手な場合は別途学習する必要があります。幾何については『螺旋本』、数え上げについては大学入試の参考書ですが『マスター・オブ・場合の数』とか。『蟻本』はほとんど使いませんでした。
おわりに
1000 問以上を埋めるのは大変でしたが、無事に終えられて安心しています。これを優先していたために、勉強したいものpriority_queueに多くのものが沈殿してしまいましたが、これから消化していきたいと思います。
そう遠くない未来に、入水記事でお会いしましょう!
以上、霧しゃまでした!
この記事が気に入ったらサポートをしてみませんか?
