
【Pythonで統計モデル】SEM7:PLSモデル
はじめに
こんにちは。株式会社GA technologiesのAISCという研究開発の部署に所属している三田と申します。
現在、私の所属しているData Scienceチームでは構造方程式モデリング(structural equation modeling: SEM)の勉強会を行っており、それに対応する形でメンバーで分担して記事を書いております。
なお、これまでは次のような記事が出ております:
【Pythonで統計モデル】SEM1:速習・構造方程式モデリング|福中公輔
【Pythonで統計モデル】SEM2:母数に関する制約|福中公輔
【Pythonで統計モデル】SEM3:パス解析(逐次モデル)|白圡義泰
【Pythonで統計モデル】SEM4:パス解析(非逐次モデル)|Masayoshi Mita
【Pythonで統計モデル】SEM5:多変量回帰分析|HAO WANG
【Pythonで統計モデル】SEM6:MIMICモデル|白圡義泰
本記事はSEM記事の7本目にあたり、PLSモデルを扱っていきます。
この「Pythonで統計モデル」の記事シリーズでは今後も各メンバーが学んだことをそれぞれ記事にしていきます。もしご興味のある方がいらっしゃいましたら、AISCのマガジンのフォローをお願いします!
なお、私はSEMについては全くの初学者になります。もし誤りなどがあればコメントでご教示いただけますと幸いです。
テキスト
本記事では豊田秀樹(2014)『共分散構造分析[R編]―構造方程式モデリング―』で扱われていた事例をPythonで再現していきます。分析用のデータは東京図書のホームページからダウンロードできます。
ちなみに、GA technologiesでは福利厚生のひとつに「テックチャージ」という素晴らしい制度があり、書籍の購入費やカンファレンスの参加費などを金額の上限なく(!)会社が負担してくれます。私は今回の勉強会にあたってSEMの本を何冊か購入しており、テックチャージ制度にかなり助けられています。
環境
本記事では次の環境のもとで分析を行っております
OS:WSL2 Ubuntu 22.04 + Docker image “python:3.10”
semopy == 2.3.9
pandas == 2.0.3
PLSモデル
図のように、観測変数x1 ~ x3の線形和で新たに潜在変数f1を作成し、観測変数x4, x5から測定された別の潜在変数f2に回帰するようなモデルがあるとします。
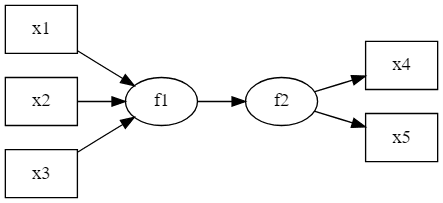
このようなモデルはPLS(Partial Least Squares)モデルと呼ばれます。
似たものでMIMICモデルや多重指標モデルなどがありますが、それらとPLSとの違いは前回のMIMICモデルの記事に説明がありますので、ご興味がおありでしたらご参照ください。
データ
先述の豊田(2014)のサンプルデータセットのうち、セミナーの満足度のデータ(seminar.csv)を使用します。
import numpy as np
import pandas as pd
import semopy
df = pd.read_csv("seminar.csv") # データの読み込み
del df["Unnamed: 0"] # この列は不要なので削除
# 書籍に合わせ、x1, x2, ..., x7に列名を置換
df.columns = [f"x{i+1}" for i in range(len(df.columns))]>>> df.head()
x1 x2 x3 x4 x5 x6 x7
0 3 5 4 5 5 5 4
1 4 4 4 5 3 4 2
2 4 4 4 4 5 4 1
3 2 3 2 2 4 2 4
4 1 1 1 1 1 1 1このデータは、あるセミナーに対しての質問紙調査のデータになります。レコード数は118件で、各変数は次のような意味になっています。
x1: テキストについての評価(1=非常に不満 ~ 5=非常に満足)
x2: 講師のプレゼンについての印象(1=非常に不満 ~ 5=非常に満足)
x3: 講義内容のペースについての評価(1=非常に不満 ~ 5=非常に満足)
x4: 質問の対処についての印象(1=非常に不満 ~ 5=非常に満足)
x5: セミナー全体の満足度(1=非常に不満 ~ 5=非常に満足)
x6: 内容はどの程度理解できたか(1=全く理解できない ~ 5=完全に理解した)
x7: 内容は目的と一致していたか(1=全く違った ~ 5=完全に一致した)
分析の実行
PLSモデルを組んでいきます。
model = semopy.Model("""
f1 ~ x1 + x2 + x3 + x4
f2 =~ x5 + x6 + x7
f1 =~ f2
f1 ~~ 0*f1
f2 ~~ f2
x1 ~~ x1
x2 ~~ x2
x3 ~~ x3
x4 ~~ x4
x1 ~~ x2
x1 ~~ x3
x1 ~~ x4
x2 ~~ x3
x2 ~~ x4
x3 ~~ x4
""")
model.fit(df, obj="MLW")ここで f1 ~~ 0*f1 は合成変数f1の分散を0に固定する指定になります。なお、このように特定の値をとるよう指定した母数は固定母数(fixed parameter)と呼ばれます。ここではf1の分散を0と固定しており、誤差を仮定しない、観測変数x1 ~ x4の単なる重み付き和としてモデリングしています。
モデルのパス図を描画してみます。
g = semopy.semplot(model, "/tmp/img.png", plot_covs=True, std_ests=True)
with g.subgraph() as s: # x1 ~ x4の位置を揃える
s.attr(rank = "same")
s.node("x1")
s.node("x2")
s.node("x3")
s.node("x4")
g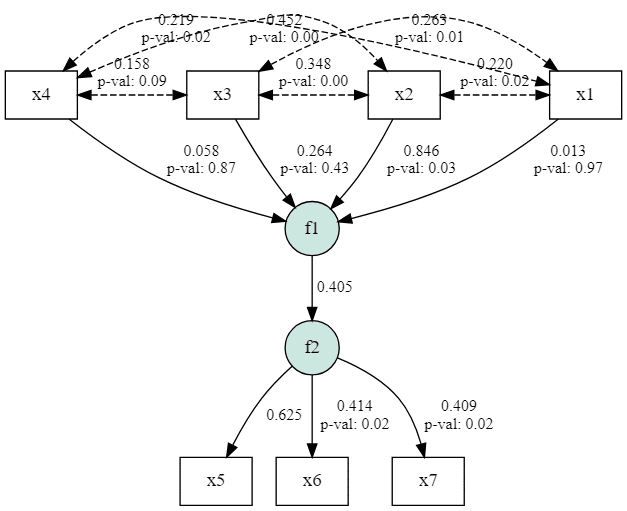
推定値について
各パラメータの推定値は次のようになりました。
>>> model.inspect(std_est=True)
lval op rval Estimate Est. Std Std. Err z-value p-value
0 f1 ~ x1 0.004464 0.012783 0.112196 0.039784 0.968265
1 f1 ~ x2 0.334864 0.845559 0.150161 2.230039 0.025745
2 f1 ~ x3 0.079364 0.264134 0.100131 0.7926 0.428011
3 f1 ~ x4 0.018456 0.058222 0.10906 0.169227 0.865618
4 f2 ~ f1 1.000000 0.405387 - - -
5 x5 ~ f2 1.000000 0.625047 - - -
6 x6 ~ f2 0.618779 0.413521 0.261841 2.363185 0.018119
7 x7 ~ f2 0.425812 0.408993 0.180843 2.354596 0.018543
8 f1 ~~ f1 0.000000 0.000000 - - -
9 f2 ~~ f2 0.650700 0.835662 0.333197 1.952898 0.050832
10 x1 ~~ x1 1.049483 1.000000 0.136631 7.681146 0.0
11 x1 ~~ x2 0.204028 0.220487 0.087232 2.33892 0.01934
12 x1 ~~ x3 0.320887 0.263098 0.116099 2.763918 0.005711
13 x1 ~~ x4 0.253523 0.219298 0.108954 2.32689 0.019971
14 x2 ~~ x2 0.815904 1.000000 0.106222 7.681146 0.0
15 x2 ~~ x3 0.374337 0.348093 0.104824 3.571092 0.000355
16 x2 ~~ x4 0.460675 0.451939 0.102975 4.473655 0.000008
17 x3 ~~ x3 1.417406 1.000000 0.184531 7.681146 0.0
18 x3 ~~ x4 0.212140 0.157899 0.125213 1.694236 0.09022
19 x4 ~~ x4 1.273476 1.000000 0.165792 7.681146 0.0
20 x6 ~~ x6 1.445375 0.829000 0.230734 6.26425 0.0
21 x7 ~~ x7 0.702839 0.832725 0.111459 6.30578 0.0
22 x5 ~~ x5 1.214418 0.609317 0.346955 3.500213 0.000465なお、Rのlavaanパッケージ(ver. 0.6.16)での推定値は次のようになります。一致する推定値が得られています。
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f2 =~
x5 1.000 0.882 0.625
x6 0.619 0.262 2.363 0.018 0.546 0.414
x7 0.426 0.181 2.355 0.019 0.376 0.409
f1 =~
f2 1.000 0.405 0.405
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f1 ~
x1 0.004 0.112 0.040 0.968 0.013 0.013
x2 0.335 0.150 2.230 0.026 0.936 0.845
x3 0.079 0.100 0.792 0.428 0.222 0.264
x4 0.019 0.109 0.170 0.865 0.052 0.058
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
x1 ~~
x2 0.204 0.087 2.339 0.019 0.204 0.220
x3 0.321 0.116 2.764 0.006 0.321 0.263
x4 0.254 0.109 2.327 0.020 0.254 0.219
x2 ~~
x3 0.374 0.105 3.571 0.000 0.374 0.348
x4 0.461 0.103 4.473 0.000 0.461 0.452
x3 ~~
x4 0.212 0.125 1.694 0.090 0.212 0.158
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.f1 0.000 0.000 0.000
.f2 0.651 0.333 1.953 0.051 0.836 0.836
.x5 1.214 0.347 3.500 0.000 1.214 0.609
.x6 1.446 0.231 6.264 0.000 1.446 0.829
.x7 0.703 0.111 6.306 0.000 0.703 0.833
x1 1.049 0.137 7.681 0.000 1.049 1.000
x2 0.816 0.106 7.681 0.000 0.816 1.000
x3 1.417 0.185 7.681 0.000 1.417 1.000
x4 1.273 0.166 7.681 0.000 1.273 1.000モデルの評価指標について
モデルのデータに対する当てはまりの指標たちは次のようになりました。RMSEA(root mean square error of approximation)は0.04と低めとなっており良好である一方、GFI(goodness of fit index)は0.898とやや低く良好とは言えません。
>>> semopy.calc_stats(model).round(3).T
Value
DoF 8.000
DoF Baseline 21.000
chi2 9.521
chi2 p-value 0.300
chi2 Baseline 92.894
CFI 0.979
GFI 0.898
AGFI 0.731
NFI 0.898
TLI 0.944
RMSEA 0.040
AIC 39.839
BIC 95.252
LogLik 0.081lavaanでの結果も一部抜粋して載せておきます。
Model Test User Model:
Test statistic 9.521
Degrees of freedom 8
P-value (Chi-square) 0.300
Model Test Baseline Model:
Test statistic 37.468
Degrees of freedom 15
P-value 0.001
Comparative Fit Index (CFI) 0.932
Tucker-Lewis Index (TLI) 0.873
Akaike (AIC) 2479.065
Bayesian (BIC) 2534.479
RMSEA 0.040
SRMR 0.045
RMSEAやUser Modelのカイ二乗値などは一致しており、これらの部分に関してはlavaanの分析結果をsemopyで再現できていることがわかります。
一方でCFIやTLIの値は一致していませんが、これはlavaanにおけるBaseline Model(独立モデル)の自由度の計算方法がsemopyとは異なるためです。今回のモデルの場合、semopyの結果にある「DoF Baseline」は21ですが、lavaanの「Model Test Baseline Model」の部分の「Degrees of freedom」は15になっております。
独立モデルの自由度について
自由度$${ df }$$は、観測変数の数を$${ p }$$、推定する母数(自由母数)の数を$${ q }$$とすると
$$
df = \frac{1}{2} p (p + 1) - q
$$
と計算されます。
semopyとlavaanの独立モデルを確認してみたところ、両者の自由母数の数qに違いがあることに気が付きました。
まずsemopyの場合、get_baseline_model() でbaseline modelを見てみると、各観測変数の分散のみを推定していることがわかります。
>>> from semopy.stats import get_baseline_model
>>> baseline = get_baseline_model(model)
>>> baseline.inspect()
lval op rval Estimate Std. Err z-value p-value
0 x1 ~~ x1 1.049483 0.136631 7.681146 1.576517e-14
1 x2 ~~ x2 0.815929 0.106225 7.681146 1.576517e-14
2 x3 ~~ x3 1.417409 0.184531 7.681146 1.576517e-14
3 x4 ~~ x4 1.273485 0.165794 7.681146 1.576517e-14
4 x6 ~~ x6 0.871876 0.113509 7.681146 1.576517e-14
5 x5 ~~ x5 0.996409 0.129721 7.681146 1.576517e-14
6 x7 ~~ x7 0.422005 0.054940 7.681146 1.576517e-14これは変数間のパスを引かず、潜在変数も計算しないモデルになっており、豊田(2014)の
すべての観測変数間に一切のパスを引かず、各変数の分散のみを自由推定するモデルを独立モデルと考えることが一般的です。
という一般的な定義通りであることがわかります。
一方でlavaanの場合でも同様の表を出してみると、次のようになりました。最初の7行は各観測変数の分散でsemopyと同様ですが、8行目以降は演算子を見る限り観測変数間の共分散を示しているようです。
> # 独立モデルのparameter table
> lav <- lav_partable_independence(fit4_P)
> data.frame(lav)
id lhs op rhs user block group free ustart exo
1 1 x5 ~~ x5 1 1 1 1 1.9928182 0
2 2 x6 ~~ x6 1 1 1 2 1.7437518 0
3 3 x7 ~~ x7 1 1 1 3 0.8440103 0
4 4 x1 ~~ x1 1 1 1 4 1.0494829 0
5 5 x2 ~~ x2 1 1 1 5 0.8159293 0
6 6 x3 ~~ x3 1 1 1 6 1.4174088 0
7 7 x4 ~~ x4 1 1 1 7 1.2734846 0
8 8 x1 ~~ x2 1 1 1 8 NA 0
9 9 x1 ~~ x3 1 1 1 9 NA 0
10 10 x1 ~~ x4 1 1 1 10 NA 0
11 11 x2 ~~ x3 1 1 1 11 NA 0
12 12 x2 ~~ x4 1 1 1 12 NA 0
13 13 x3 ~~ x4 1 1 1 13 NA 0自由母数の数を求める関数 lav_partable_npar() に通してみると、自由母数の数は13と計算されます。
> # 自由母数の数
> lav_partable_npar(lav)
[1] 13自由度の計算式$${ df = \frac{1}{2} p (p + 1) - q }$$のうち、$${ \frac{1}{2} p (p + 1) }$$ は今回のモデル($${ p=7 }$$)だと28になりますので、
semopyだと$${ q = 7 }$$のため$${ df = 28 - 7 = 21 }$$
lavaanだと$${ q = 13 }$$のため $${ df = 28 - 13 = 15 }$$
という計算がなされ、その結果として先述のようなカイ二乗値や自由度の出力結果になったのではないかと推測しております。
独立モデルの定義を一致させてみる
lavaanはユーザーが自分で定義したBaseline Modelを投入してモデルの評価を行うこともできるため、「観測変数の分散のみを推定する」というsemopyと同一の定義のモデルをbaselineに設定してみます。
> # semopy同様、分散だけを推定するbaseline modelにする
> user_defined_baseline <- '
+ x1 ~~ x1
+ x2 ~~ x2
+ x3 ~~ x3
+ x4 ~~ x4
+ x5 ~~ x5
+ x6 ~~ x6
+ x7 ~~ x7
+ '
> baseline <- sem(user_defined_baseline, data=data4, fixed.x=F)
> fitMeasures(fit4_P, baseline.model=baseline)["baseline.df"]
baseline.df
21
> fitMeasures(fit4_P, baseline.model=baseline)["baseline.chisq"] |> round(3)
baseline.chisq
92.894semopyと同一の自由度とカイ二乗値を得ることができました。
独立モデルが共分散を推定するのはfixed.x = FALSEのとき?
lavaanの独立モデルが共分散も自由母数として扱っていると述べましたが、常にそうするわけではないようです。いろいろ試したところ、fixed.x = FALSEをつけて推定したときにそうなるように見えます。そして、豊田(2014)のRのコードではfixed.x=FALSEで推定しています。
このfixed.xという引数は分析時のモデル(User Model)にて外生変数の分散や共分散を推定するかどうかを指定するオプション引数になります。fixed.x=Fにしているおかげでlavaanではsemopyのようにx1 ~~ x1といった指定をいちいち明示しなくてもまとめて推定してくれているわけです。
もしfixed.x=Tに設定してsemopyと同様にmodelにx1 ~~ x1のような明示をモデルのformulaに書くと、semopyと独立モデルは分散のみが自由母数になり、semopyの結果と同じ自由度(baseline.df = 21)とカイ二乗値(baseline.chisq = 92.894)になります。
> # fixed.x=TRUEにしてformulaに分散・共分散を指定
> pls <- 'f1 ~ x1 + x2 + x3 + x4
+ f2 =~ x5 + x6 + x7
+ f1 =~ f2
+ f1 ~~ 0*f1
+ f2 ~~ f2
+ x1 ~~ x1
+ x2 ~~ x2
+ x3 ~~ x3
+ x4 ~~ x4
+ x1 ~~ x2
+ x1 ~~ x3
+ x1 ~~ x4
+ x2 ~~ x3
+ x2 ~~ x4
+ x3 ~~ x4'
> fit <- sem(pls, data=data4, fixed.x=TRUE)> # 独立モデルのパラメータ表
> lav <- lav_partable_independence(fit)
> data.frame(lav)
id lhs op rhs user block group free ustart exo
1 1 x5 ~~ x5 1 1 1 1 1.9928182 0
2 2 x6 ~~ x6 1 1 1 2 1.7437518 0
3 3 x7 ~~ x7 1 1 1 3 0.8440103 0
4 4 x1 ~~ x1 1 1 1 4 1.0494829 0
5 5 x2 ~~ x2 1 1 1 5 0.8159293 0
6 6 x3 ~~ x3 1 1 1 6 1.4174088 0
7 7 x4 ~~ x4 1 1 1 7 1.2734846 0
> fitMeasures(fit)["baseline.df"]
baseline.df
21
> fitMeasures(fit)["baseline.chisq"] |> round(3)
baseline.chisq
92.894LavaanのBaseline Modelはなぜ共分散も自由母数としているのか
lavaanでfixed.x=FALSEにして推定したときの「観測変数間の共分散も推定する」という独立モデルの定義がどういった考え方に基づくものなのかは、軽く調べてみたものの今のところわかっておりません。
より保守的な値になるため、慣習的にそうしているのかもしれません。
今後はそのあたりのトピックも気にしつつSEMを勉強していきたいと思います。
今後について
本記事シリーズでは今後もPythonでSEMを実践していきます。次回は宋さんが二次因子分析モデル・階層因子分析モデルを紹介する予定です。ご興味のある方はぜひAISCのマガジンのフォローをお願いします!
参考文献
豊田秀樹(2014)『共分散構造分析[R編]―構造方程式モデリング―』、東京図書。
