
フィッシャー情報量、どんなイメージ?
はじめに
私の所属している研究室ではprml(パターン認識と機械学習)の輪読を行っています。ちょうど6章が私の担当会で準備をしていたのですがフィッシャー情報量が登場しました。フィッシャー情報量自体は情報幾何を勉強した時に何度か目にしたことがありますがよくわからず頓挫。特になぜそれが"情報量"と呼ばれるのかイメージがうまくできず苦労しました。今回、輪読の担当ということをあり本腰を入れて勉強したところ今までとだいぶ異なる視点で見ることができるようになったのでここにまとめようと思います。
フィッシャー情報量の定義
まずはフィッシャー情報量の定義を見ていきます。ある分布から生成されたn個のサンプルを$${\textbf{x}=\{x_1,x_2,...x_n \}}$$とします(Riemann計量としてのフィッシャー情報量(情報行列)の計算はサンプル数1としている場合が多いですが今回は一般的な定義に則ります)。この時、対数尤度関数は次のように書くことができます。
$$
logL(\theta ; \textbf{x})=\Sigma_{i=1}^{n}logp(x_i|\theta)
$$
さて、この尤度関数はパラメータθで定義づけられていますが、これをパラメータθで微分した関数をスコア関数V(θ;x)と呼ぶことにします。
$$
V(\theta;\textbf{x})=\frac{\partial}{\partial \theta}logL(\theta;\textbf{x})
$$
このスコア関数はイメージどおり尤度関数の傾きを表しています。最尤推定解はスコア関数が0となるときのθの値というわけです。
さて問題のフィッシャー情報量 I(θ)ですがこのスコア関数から計算されます。計算式は以下の通りです。
$$
I(\theta)=E_{\theta}[(V(\theta;\textbf{x}))^2]=\int(V(\theta;\textbf{x}))^2p(\textbf{x};\theta)d\textbf{x}
$$
これがフィッシャー情報量の定義式です。スコア関数の二乗の期待値であることはわかりますが、いったいこれが何を意味しているのか、またどうしてこれが"情報量"であるのか、ぱっと見では理解しにくいかなと思います。以下ではもう少しこれをかみ砕きながら説明をしていきます
対数尤度関数の形はサンプリングごとに異なる
フィッシャー情報量の定義の説明をする前に対数尤度関数の基本的な事項について確認をしていきます。まず対数尤度関数ですが、サンプリングされたデータをもとに計算されるため、サンプリングごとに関数形は違ってきます。もちろん対数尤度関数の最大値は真値と近い値を取るはずなので最大値は真値あたりに存在するわけですが、サンプリングごとにそれが右にいったり左にするわけです

真値における傾きは
さて、先ほどの図をもとに真値における傾きを考えていきます。もちろん真値なんてわからないですし、わからないからこそ尤度関数を計算しているわけですが、仮に分かったらという体で話を進めます。先ほど説明したように尤度関数はサンプリングごとに形が違うわけですが、もちろんたまたま真値あたりでピークを持つ場合もあり得るでしょう。その場合、下の図のように真値における傾きは0になります。もし尤度関数のピークが真値より右にずれていたら真値における傾きは正になりますし、左にずれていれば負になります。

真値における傾きは0になったり正負になったりするが期待値は0
このように、対数尤度関数の真値における傾きはサンプリングごとに0、正、負を取っていくわけですが、期待値を取るとどうなるでしょうか。0になりそうですね。これは間違っていなくて、実際に数学的に証明することが可能です。これはより数学的ないい方をすれば、真値におけるスコア関数の期待値は0ということができ、以下の式で表されます。
$$
E_{\theta}[V(\theta;\textbf{x})]=\int V(\theta;\textbf{x})p(\textbf{x};\theta)d\textbf{x}=0
$$
数学的な証明は様々なところで見ることができると思いますのでここでは省略しますが、証明自体はかなり簡単です。
真値における傾きの分散はとがり具合を反映
さて、真値における傾きは0になったり正、負になることは先ほど見てきたとおりですが、このように色々な値を取る場合、その分散を計算することが可能です。つまり対数尤度関数の真値のおける傾きの分散、が計算できるわけです。具体的な計算は少しおいておき、先に次の画像の対数尤度関数を考えます。
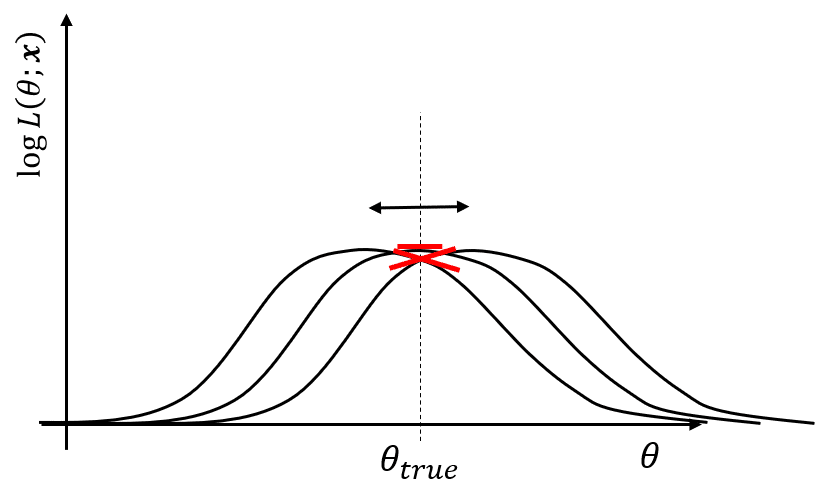
真値における傾きの分散は先ほどより小さい
先ほどより緩い対数尤度関数です。同じようにサンプリングごとに関数形が変わるため、左右にピークが振れています。さて、この時の傾きの分散と先ほどのとがった対数尤度関数の傾きの分散を比べてみましょう。どちらの方が大きくなるでしょうか。例えば左に同じだけずれたとしても鋭くとがった対数尤度関数の方が真値における傾きは大きくなりますよね。そのことから先のとがった対数尤度関数の方が真値における傾きの分散は大きくなることが分かります。
つまり、
真値における傾きの分散=対数尤度関数のとがり具合
であることがわかります。
とがり具合はデータが持つパラメータの情報量
さて、対数尤度関数はデータからパラメータを決めるための関数でした。対数尤度関数からパラメータを推定する場合は傾きが0になるところで値を取りますので一意に推定値は決定するわけですが、とがり具合が緩やかな場合は推定値の周辺の値も高い対数尤度の値を持ちますので、推定値の候補がたくさんあるわけです。つまり曖昧ということです。一方、するどくとがっている場合はピークの推定値以外は候補にすらなれないわけですからかなりはっきりと候補が決まっている状態です。候補が少ないということは確信をもって推定された値を真値だと言えるわけですから、データが持っていたパラメータに関する情報量が多かった、ということになりますね。つまり対数尤度関数がとがっている方が"データが持っているパラメータに対する情報"が多いわけです。
さて、先ほど言ったように、傾きの分散は鋭さを反映しているわけですから、
対数尤度関数の真値における傾きの分散=データが持っているパラメータに対する情報量
ということができそうです。
真値における傾きの分散=フィッシャー情報量
ここまでくればフィッシャー情報量まであと一歩です。
真値における傾きの分散が重要である、というのが今までの結論でしたが、実際にこれを式で表すと以下のように書けるでしょう
$$
Var(V(\theta;\textbf{x}))=E_{\theta}[(V(\theta;\textbf{x}))^2]-(E_{\theta}[V(\theta;\textbf{x})])^2
$$
二乗の期待値-期待値の二乗、ですね。ところが真値における傾きの期待値は0になることを先ほど見ましたね。ですので第二項目は0になり
$$
Var(V(\theta;\textbf{x}))=E_{\theta}[(V(\theta;\textbf{x}))^2]
$$
はい、フィッシャー情報量が出てきました。つまりフィッシャー情報量とは真値における傾きの分散であり、データが持つパラメータに対する情報量を計算しているに他ならなかったわけです。
まとめ
今回はフィッシャー情報量がなぜ情報量と呼ばれるのか、の直観的な理解を対数尤度関数の傾きの分散という観点から説明を試みました。個人的には傾きは傾きでも真値における傾きであること、を意識することが非常に重要であると思っています。
クラメールラオの不等式や情報幾何の計量など、様々なところで顔を出すフィッシャー情報量への理解がこの記事を通してより深まれば幸いです。
