ソフトマックス（Softmax）とは

ソフトマックス関数（softmax function）は、機械学習で画像などを複数クラス（種類）に分類する問題を解くためによく使われます。今記事では、ソフトマックスの意味と計算方法を解説します。

画像分類

例えば、次のような画像があるとします。

画像のクラスとしては、以下が可能だとします。

• イヌ

• ネコ

• サル

• トリ

• カニ

人間が判断すれば、ほとんどの人がサルの可能性が高いと判断するでしょう。

これを機械学習によって判断したいとします。このようなタスクは画像分類と呼ばれます。モデルは数値しか扱えないのですが、どのようにして画像がサルだと判断するのでしょうか。

Argmaxとは

画像のデータを入力として、モデルは各クラスに対して数値を出力します。

この数値が高い動物ほど正解のクラスである可能性が高くなります。この例ではサルの数値が2.5で一番高い数値なので、サルを予測していることになります。

このように予測値の一番高いクラスを選ぶことを最大点を与える要素を選ぶという意味で最大点作用素あるいはargmax(arg max)と呼びます。

argmaxを確率として解釈すると、サルが100％で残りは全て0%になります。なぜならば、argmaxでは最大値になる要素を一つ選ぶだけだからです。

なので、argmaxはハードマックス（hardmax)とも呼ばれます。はっきりとした区別を行う感じがあります。

Softmaxとは

しかし、モデルが出す数値にはそれ以上の情報が含まれています。例えば、画像がイヌである可能性はトリやカニより高いのが数値の差からわかります。しかし、これらの数値を見ただけでは、どのくらい高いのかがははっきりとはわかりません。

よって、これらを確率として表現できることが望まれます。

ところが、モデルが出す数値には負の値も含まれるので、単純に全てを足し合わせて割合を計算するわけにもいきません。なので、まず全ての数値を指数関数$${e^x}$$に渡して正の値にします。指数関数は$${\exp(x)}$$とも表記します。

以下の図が示すように、指数関数はどのような値$${x}$$に対しても正の値を返します。また、より大きい$${x}$$の値に対してより大きい正の値を返します。なので値の相対的な大小が保存されます。

指数関数$${e^x}$$

よく「指数関数的に増加する」と言った表現が使われますが、上図からもわかるように入力値の増加に対して指数関数値の増加率はどんどん大きくなっています。

このため指数関数は単に数値を正の値にするだけでなく、より大きい入力値をより強調して正の値にしています。例えば、入力値が−4だとほぼ指数関数値はほぼ０になりますが、入力値が4だと約54.6でグラフからはみ出てしまいます。

より大きい数値は強調され、より小さい数値はほぼゼロになる特徴があります。

あるクラスの値が他のクラスより大きくて、他のクラスが全て小さい場合、一つのクラスだけ突出して大きくなり、他のクラスに対してはほぼ０となるのでargmaxのようにはっきりとした区別を行うのと似ています。

しかし、このままだと、確率としての解釈ができないの次のように割合を計算します。指数関数を使って正の値に変換された予測値を足し合わせた全体の値で、各クラスの指数関数値を割り算します。これが各クラスに対する予想確率になります。

こうしてみると、イヌの確率がトリやカニよりずっと高いのがわかります。また、イヌの確率はサルの確率より遥かに低いことも見て取れます。

Softmaxの計算方法

これを数式として書くと以下になります。

$$
f(クラス=i \mid 画像) = \dfrac{e^{x_i}}{\sum\limits_{k=1}^n e^{x_k}}
$$

これはある画像を与えられた時のクラスが$${i}$$である確率を計算しています。

ここで$${i}$$は番号によって{イヌ、ネコ、サル、トリ、カニ}の中の一つのクラスを指します。また、$${x_i}$$は、そのクラスに対するモデルの出力値になります。$${n}$$はクラスの数に相当します。この例では$${n=5}$$ですね。

一見複雑に見えますが、指数関数を使っている部分を$${z_i = e^{x_i}}$$とすると、

$$
f(クラス=i \mid 画像) = \dfrac{z_i}{\sum\limits_{k=1}^n z_k}
$$

分母は全ての指数関数値を足し合わせており、分子は一つのクラスの指数関数値なので単純に割合を計算していることになります。

よって、各割合は0から1の値を取り、割合の合計は1になります。つまり、確率としての解釈が可能になっています。hardmaxのように0と1だけではなく、さまざまな値を取りクラス間の予測値を確率として比較することが可能です。

この数式をソフトマックス関数と呼びます。

まとめると、ソフトマックス関数は各クラスに対してモデルが出力したスコアをもとに、各クラスの確率を求めることができます。

Softmaxは自信度でもある

確率と呼びましたが、サイコロを何度も振ることによって統計をとるような確率とは異なります。むしろ、モデルが出力した値を確率の形式にしたという感じです。各クラスに対する割合の和が１になるように正規化（標準化)をしているだけとも言えます。

また、モデルの予測に対するソフトマックスの出力は、モデルの自信の度合いを表しているという解釈もできます。

例を見てみましょう。以下の画像に対してのモデルの出力からは、イヌかネコかをはっきりと判断していないのがわかります。

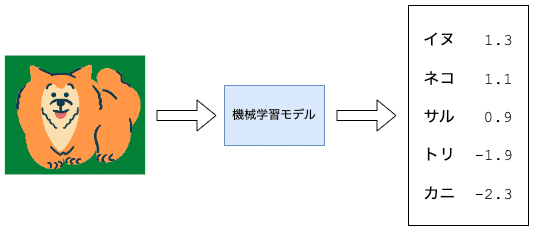
これをソフトマックスで割合に変換します。

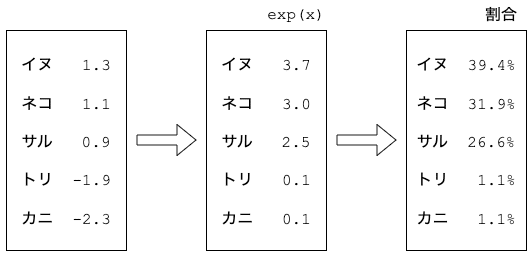
この割合を見比べると、イヌがダントツで高いわけでもないことがわかります。つまり、この画像に対してモデルの自信度はあまり高くないと言えるでしょう。

モデルによる確率予測としてとらえると、イヌである確率は39.4%という解釈になります。モデルの自信度と考えると、39.4%しか自信がないと言えます。

この辺は文脈によって使い分けられているので論文などを読む場合に、確率や自信度などの言葉が出てきても、両方ともソフトマックスによって正規化された値に対する解釈と考えれば矛盾は生じません。

まとめ

ソフトマックス関数は、複数クラス分類問題でよく使われるます。

ソフトマックスの計算方法は、モデルからの出力値を指数関数を使って正の値にしてから各クラスの割合を計算します。それを確率や自信度と解釈します。ただし、実際に実験を繰り返して頻度を計算するわけではありません。

ニューラルネットワークを使って分類タスクを行う場合は、最終層においてソフトマックスを使うことが多いです。

関連記事