微分と偏微分と勾配

ディープラーニングでよく使われる計算として微分があります。微分がわかると、偏微分や勾配についても理解が進むのでディープラーニングの訓練で何が起きているのか理解しやすくなります。

もちろん、微分の計算ができなくともディープラーニングのモデルを構築することはできますが、多くの解説記事などでは微分、偏微分、勾配といった概念が登場するので、ある程度は内容を知っていた方が便利です。

微には「細かい」とか「小さい」という意味があります。分は「分ける」とか「部分」といった言葉に登場します。よって、微分という名前には「小さく分ける」という意味が込められています。

この記事では、微分とは何なのかについて、そして偏微分と勾配との関係を解説します。

関数の変化率と区間

関数の変化率

下のグラフを見てください。$${y}$$は$${x}$$の関数です。

$$
y = f(x)
$$

$${x}$$を$${x_1}$$から$${x_2}$$へと移動すると、$${y}$$が$${y_1}$$から$${y_2}$$へと値が変わります。この変化率は次のように定義できます。

$$
\dfrac{\Delta y}{\Delta x} = \dfrac{y_2 - y_1}{x_2 - x_1}
$$

ここで、$${\Delta y = y_2 - y_1}$$と$${\Delta x = x_2 - x_1}$$としています。$${\Delta}$$はデルタと呼びます。

変化率と区間

$${\Delta x}$$を小さくとると、$${y_2}$$の位置が変わるので変化率も変わります。

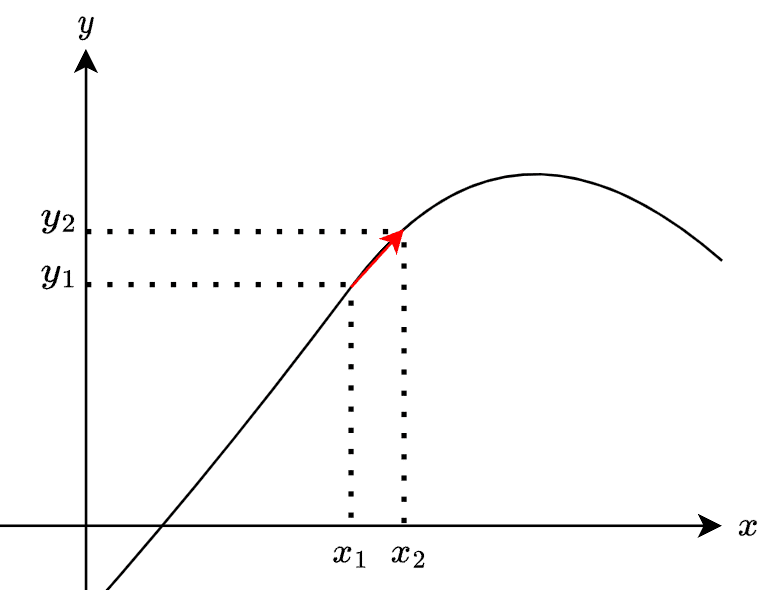
$${\Delta x}$$が小さくなるほど、変化率$${\dfrac{\Delta y}{\Delta x}}$$は$${x_1}$$における関数$${y=f(x)}$$の傾き（接線）へと近づきます。

１次関数

具体的に、関数$${f(x)}$$として、次の直線を考えます。

$$
y = a x + b
$$

すると変化率は、

$$
\dfrac{\Delta y}{\Delta x} = \dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{(a x_2 + b) - (a x_1 + b)}{x_2 - x_1} = \dfrac{a (x_2 - x_1)}{x_2 - x_1} = a
$$

となり、直線の傾きと同じになります。１次関数では変化率は一定なので$${\Delta x}$$によらず固定値となります。

２次関数

では、次の２次関数ではどうでしょうか。

$$
y = x^2
$$

変化率を計算します。

$$
\dfrac{\Delta y}{\Delta x} = \dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{x_2^2 - x_1^2}{x_2 - x_1} = \dfrac{(x_2 - x_1)(x_2 + x_1)}{x_2 - x_1} = x_2 + x_1
$$

$${y = x^2}$$の$${x_1}$$から$${x_2}$$への変化率は、$${x_1 + x_2}$$であることがわかります。

では、$${\Delta x}$$をもっと小さくするとどうなるでしょうか。

微分の計算

区間を極限まで小さく

では区間$${\Delta x}$$をどんどん小さくして０へと近づけましょう。

なお、$${\Delta x}$$が小さい時は$${\delta x}$$と書くことが多いです。$${\delta}$$もデルタですが小文字になっています。

変化率は次のように書けます。

$$
\dfrac{\delta y}{\delta x}
$$

ここで、$${\delta y = y_2 - y_1}$$で$${\delta x = x_2 - x_1}$$です。

なので$${\Delta x}$$でも$${\delta x}$$でも同じですが、$${\delta x}$$だと小さい区間というニュアンスが込められています。

微分の計算

さらに、$${\delta x}$$を限りなく0に近づけることを考えます。

$${\delta x}$$を限りなく0に近づけた時の$${\dfrac{\delta y}{\delta x} }$$の値を次のように表現します。

$$
\lim\limits_{\delta x \rightarrow 0} \dfrac{\delta y}{\delta x}
$$

$${\lim}$$はリミット（limit）で極限とか限界を意味します。よって、$${\lim\limits_{\delta x \rightarrow 0}}$$とは「$${\delta x}$$を限りなく0に近づける」という意味です。

これは関数$${f(x)}$$のある点における傾きになります。

実は、$${\lim\limits_{\delta x \rightarrow 0} \dfrac{\delta y}{\delta x} }$$は微分の計算を意味し、次のように$${\dfrac{dy}{dx}}$$という表記をします。

$$
\dfrac{dy}{dx} = \dfrac{df(x)}{dx} = \lim\limits_{\delta x \rightarrow 0} \dfrac{\delta y}{\delta x}
$$

これを$${x}$$による$${f(x)}$$の微分と呼びます。

「微分する」とは、$${f(x)}$$のある点における傾きを計算することを意味します。なお、計算されたものを微分係数とも呼びます。

また、次のように微分を表現する表記にはいろいろあります。

$$
\dfrac{dy}{dx} = y' = \dfrac{df(x)}{dx} = f'(x)
$$

物理などでは、次のような表記もします。

$$
\dfrac{dy}{dx} = \dot{y} = \dfrac{df(x)}{dx} = \dot{f}(x)
$$

これらの省略形の表現ができるのは、$${y = f(x)}$$が$${x}$$だけに依存する関数だからです。あとで見るように複数の変数がある場合は表記の仕方が変わってきます。

なお、微分の値は関数のある点における傾きなので、計算する時の$${x}$$の値によって変わります。

よって、$${x_1}$$における微分であることを強調するには次のようも表現できます。

$$
\dfrac{dy}{dx} \bigg\vert_{x = x_1} = \dfrac{df(x_1)}{dx} = f'(x_1)
$$

２次関数の微分

繰り返しますが、２次関数の変化率は次のようになっていました。

$$
\dfrac{\Delta y}{\Delta x} = \dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{x_2^2 - x_1^2}{x_2 - x_1} = \dfrac{(x_2 - x_1)(x_2 + x_1)}{x_2 - x_1} = x_2 + x_1
$$

区間が小さくても同じです。

$$
\dfrac{\delta y}{\delta x} = \dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{x_2^2 - x_1^2}{x_2 - x_1} = \dfrac{(x_2 - x_1)(x_2 + x_1)}{x_2 - x_1} = x_2 + x_1
$$

ここで$${\delta x}$$を限りなく小さくするとは、$${x_2}$$を$${x_1}$$に限りなく近づけることになります。

$$
\dfrac{dy}{dx}\bigg|_{x=x_1} = \lim\limits_{x_2 \rightarrow x_1} \dfrac{\delta y}{\delta x} = \lim\limits_{x_2 \rightarrow x_1} (x_2 + x_1) = 2 x_1
$$

となります。つまり、$${x^2}$$の$${x_1}$$における微分は$${2 x_1}$$です。

$${\delta x = x_2 - x_1}$$ですが、より一般に$${x_1}$$を$${x}$$で置き換えると、$${ x_2 = x + \delta x }$$になり、次のように書き直せます。

$$
\dfrac{ df(x)}{dx} = \lim\limits_{\delta x \rightarrow 0} \dfrac{\delta y}{\delta x}  = \lim\limits_{\delta x \rightarrow 0} (x + (x+\delta x)) = 2x
$$

さまざまな関数で、微分を計算することができます。ただし、微分が計算できる関数には条件があります。

微分ができる条件

関数が連続である区間

微分ができるのは、関数$${f(x)}$$が連続である区間に限ります。

例えば、以下の関数は点$${x_1}$$で不連続なので、$${x_1}$$での微分はできません。他の連続な部分での微分は可能です。

関数が定義できる区間

あと、関数が定義されていない区間で微分はもちろん不可能です。

例えば、関数$${f(x) = \dfrac{1}{x - 1}}$$は$${x = 1}$$で定義されていないので$${x = 1}$$では微分できません。

微分が一定値である

微分の値が一つに定まらないケースも、微分ができません。

例えば、活性化関数としてよく使われるReLUは$${x=0}$$では微分ができません。

$$
\text{ReLU}(x) = \max(0, x)
$$

実用では$${x=0}$$における$${\text{ReLU}}$$の微分は$${\dfrac{d \text{ReLU(x)}}{dx}\bigg|_{x=0} = 1}$$と決めることで対応します。

偏微分とは

複数変数の関数

偏微分は、関数が複数の変数を持つ場合に各変数に対して定義します。

例えば、関数$${z = f(x, y)}$$に関しては$${x}$$と$${y}$$に対してそれぞれ微分を別々に考えるのですが、これを偏微分と呼びます。

偏微分は次のように定義します。

$$
\dfrac {\partial z}{\partial x} = \dfrac{\partial f(x, y)}{\partial x} = \lim\limits_{\delta x \rightarrow 0} \dfrac{f(x + \delta x, y) - f(x, y)}{\delta x}
$$

つまり、$${x}$$で$${f(x, y)}$$を偏微分する時に、$${x}$$だけに関して極小の変化を考えますが、それ以外は固定されているとみなします。

そのため、$${\partial}$$という記号を使って、「この関数は$${x}$$だけに依存するわけではなく他にも変数がある」ことを暗示しています。

同様に、$${y}$$で$${f(x, y)}$$を偏微分するのは、次のように定義できます。

$$
\dfrac {\partial z}{\partial y} = \dfrac{\partial f(x, y)}{\partial y} = \lim\limits_{\delta y \rightarrow 0} \dfrac{f(x, y + \delta y) - f(x, y)}{\delta y}
$$

損失関数の偏微分

もちろん、ニューラルネットワークのように、たくさんのパラメータ（重み）がある場合でも偏微分の考え方は同じです。

それぞれのパラメータに対して損失関数の偏微分を行います。それによって、各パラメータを微調整するとどのくらい損失関数に影響を与えるのかがわかるからです。

例えば、損失関数をパラメータの関数として、$${\text{loss}(\boldsymbol{w})}$$と表現します。ここで、$${\boldsymbol{w} = (w_1, w_2, \dots, w_n)}$$となります。

各パラメータによる損失関数$${\text{loss}(\boldsymbol{w})}$$の偏微分が計算できれば、どの方向に各パラメータを調整すれば損失値が小さくなるのかがわかります。

損失値が小さくなるようにパラメータ$${w_1}$$を調節するの更新式は次のように書けます。

$$
w_1 \leftarrow w_1 - \alpha \dfrac{\partial \text{loss}(\boldsymbol{w})}{\partial w_1}
$$

$${\alpha}$$は学習率です。

さらに、全てのパラメータの更新式をまとめて表記するには勾配を使います。

勾配とは

勾配とは、ある関数における全ての偏微分をベクトルとしてまとめたものです。計算式がコンパクトになるなどの利点があります。

$$
\text{grad} f(x, y) = \left( \dfrac{\partial f(x, y)}{\partial x},  \dfrac{\partial f(x, y)}{\partial y} \right)
$$

また、次のようにナブラ記号を使うこともよくあります。

$$
\nabla f(x, y) = \left( \dfrac{\partial f(x, y)}{\partial x},  \dfrac{\partial f(x, y)}{\partial y} \right)
$$

これを使うと全てのパラメータの更新を次のように書き表せます。

$$
\boldsymbol{w} \leftarrow \boldsymbol{w} - \alpha \nabla \text{loss}(\boldsymbol{w})
$$

なお、数学的に厳密な話でない限り、微分と偏微分と勾配を全て同じような意味合いで使うことが見受けられます。その場合は、文脈で判断するしかありません。

関連記事