言語AIの進化史⑩隠れマルコフモデル

前回は、バイト対符号化（BPE）を紹介しましたが、今回はトークン化から離れて、シーケンスデータを扱う手法に焦点を当てていきます。

シーケンスデータ（Sequence Data）とは、順番に並んだデータのことです。もっというと、データの並び方に何らかの意味や情報が含まれているデータ列です。

例として、シーケンスデータとは次のようなものを指します。

• 株価の時系列データ

• 文章のテキストデータ

• スピーチの音声データ

これらのシーケンスデータは、どれもデータが順番に並んでおり、その順番には意味や情報が含まれています。

たとえば、株価の変動は前の値からの影響を受けます。文章の流れでは文脈が次の単語を決定します。音声データも音素の並びに依存して意味が形成されます。

音素は、言語の音を構成する最小の単位です。

参考：音素 - Wikipedia

そのため、順番に生じる各々のデータ（株価、単語、音素）を独立したものとして扱うと正確な理解ができません。

よって、シーケンスデータを解析するためのアプローチが必要となります。

そんな中でも、今回は隠れマルコフモデル（Hidden Markov Model、HMM）を紹介します。

マルコフモデル

まずは、マルコフモデルの一般的なアプローチを解説します。

ヒストリーをどこまで扱うべきか

まず、予測のために過去の観測データのシーケンス（ヒストリー）をどこまで遡さかのぼって扱うべきかを考えます。

ヒストリー（過去の観測データのシーケンス）

たとえば、株価予測や音声認識では、過去のデータを基に次の値を予測します。もちろん、過去といっても非常に古い情報は必要ありません。

また一般的に、直近のデータがより重要であり、遠い過去のデータは次の未来に与える影響が少ないと考えられます。つまり、シーケンスデータを処理する際には、全てのヒストリーが必要とは限らない場合が多いです。

直近（赤枠）と遠い過去（青色）の影響

具体例として、天気の観測情報を考えましょう。観測値のシーケンスを次のように定義します。

$$
x_1, x_2, \ldots, x_i
$$

ここで、$${x_i}$$は$${i}$$番目の天気の状態を表します。たとえば、気圧、温度、湿度、降雨量などが含まれるベクトルとして扱います。

このようにして集めたヒストリーから次の状態を予測することができます。これを数式で表現すると、次のようになります。

$$
P(x_{i+1} \mid x_1, x_2, \ldots, x_i)
$$

この式は、これまでの観測データ（ヒストリー）に基づいて次の状態を予測する条件付き確率を表しています。この条件確率が最も高い状態が、次の予測値となります。

下図はこれを表現したものです。

ヒストリー全体から計算すると複雑になっていく

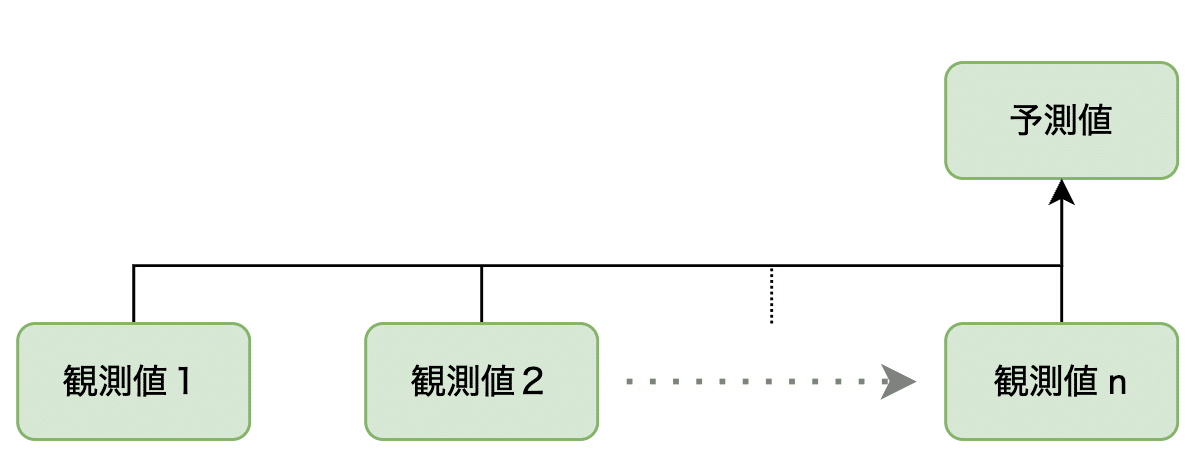
しかし、次の天気を予測する際、どの程度のヒストリーが本当に必要でしょうか？

非常に古いデータまで遡さかのぼると、計算量やメモリ消費が膨大になり、モデルの複雑さが増してしまいます。よって、効率的な予測モデルを構築するためにも、できるだけ直近のデータだけを使用することが望ましいです。

それでは、どの時点からヒストリーを切り捨てるべきでしょうか？

これは簡単には決められませんが、次にこれを解決する方法について考えてみましょう。