scikit-learn機械学習②線形回帰：理論編

線形回帰は、観測値などのデータの集まりから関係を見つけ出し、その関係を用いて新しいデータの値を予測する統計的な手法です。線形回帰では、データが直線上に近似的に配置されるような関係を探します。

例えば、以下のデータ点の集まりを見て$${x}$$と$${y}$$の間には直線的な関係があるのがわかります。

しかし、このような関係を説明できる直線はたくさんあるようにも見えます。

そこで、データを直線的な関係で最もよく説明するためのモデルが線形回帰モデルとなります。なお、線形回帰をディープラーニングで実装することもできます。そちらに興味がある方は、こちらの記事を参照してください。

しかし、「最もよく説明する」とはどういうことでしょうか。

この記事では、ディープラーニングを使わずに線形回帰モデルを解く方法を解説します。

単純線形回帰

前述の図では、$${x}$$と$${y}$$の間に直線的な関係があります。便宜上、$${y}$$の値が$${x}$$によって決まるとします。その際、$${x}$$は入力（独立）変数、$${y}$$は出力（従属）変数と呼ばれます。

直感的には、$${x}$$の値が変化すると、それに従って$${y}$$の値が変化するというイメージになります。ここでは、そこに因果関係があるかどうかまではわかりません。しかし、直線的な相関があるのは見て取れます。

このような関係を求めることを線形回帰と呼びます。また、入力変数が一つの場合の線形回帰を単純線形回帰と呼びます。

我々が知りたいのは入力$${x}$$と出力$${y}$$の間の直線的な関係をどう表現するかです。その関係を使って未経験の入力$${x}$$に対して出力$${y}$$を予測することが可能となります。仮に、国民全体の身長と体重の間の関係にはある程度の直線的な関係があるとしたら、線形回帰を適用して予測することはある程度有効だと考えられます。

もちろん、新しいデータが線形の関係からは程遠いものになる可能性はあります。例えば、株価などはある期間で直線的な変化をしていても途中から急落や急騰することはしばしばあります。実際株価は時間だけでなく、たくさんの外的要因に左右されるので時系列で見るとむしろ非線形なのが普通です。よって、線形回帰を適用する際には、データに関してある程度の知識があり、直線的な関係を使うことが妥当だと考えられるケースだけになります。

では次に、入力$${x}$$と出力$${y}$$の間の直線的な関係を表現します。

直線は$${y = ax + b}$$という式で表されます。ここで、$${a}$$ は直線の傾き（独立変数$${x}$$の変化に対する従属変数$${y}$$の変化率）、$${b}$$ はy切片（直線がy軸と交わる点）です。

よって、単純線形回帰の直線を決めるとは、その傾き$${a}$$と切片$${b}$$という２つのパラメータを求めることに他なりません。また、そのパラメータによる直線を回帰直線と呼びます。

しかし、どのようなデータにも測定の際の不備などによってある程度のエラーがあります。そのため理論上は直線的な関係があるとしても実際のデータが完全な直線に沿っていないことも多いでしょう。よって、線形回帰では与えられたデータをできるだけ誤差を小さくして説明できる直線を見つけることになります。

そこで最小二乗法が登場します。

最小二乗法

線形回帰における誤差の最小化は、最小二乗法（Least Squares Method）という手法で行うことができます。最小二乗法は、各データ点と回帰直線との間の距離（誤差）の二乗の合計が最小になるように、直線の傾き $${a}$$ と切片 $${b}$$ を決定します。この合計値を最小にすることで、データに最も適合する直線を見つけ出すことができます。

データと回帰直線との誤差

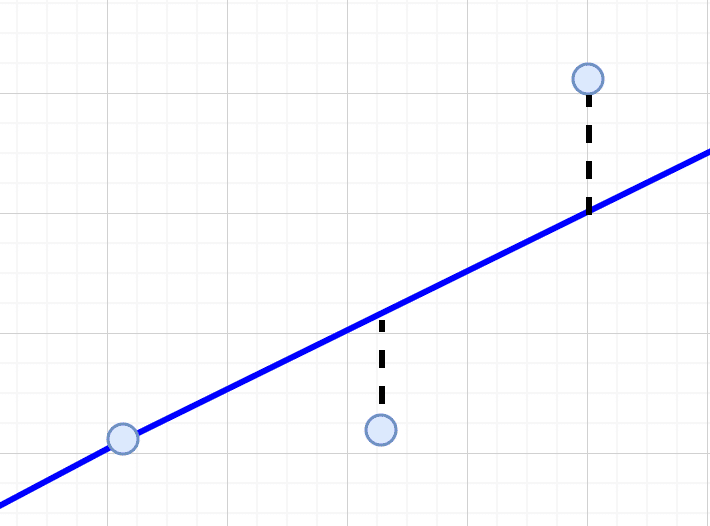
データセットが $${(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)}$$ という$${n}$$個の点で構成されているとします。データが2点しかなければ簡単に直線を引けますが、データが3点以上ですべてを直線上に収めることができない場合はできるだけ全ての点が回帰線に近くなることを目指します。

各データ点に対する誤差（または残差）は、実際の$${y}$$値とモデルによる予測値 $${ax + b}$$ との差です。つまり、$${i}$$番目のデータ点における誤差は $${y_i - (ax_i + b)}$$ です。

最小二乗法では、これらの誤差の二乗の合計を最小化することを目指します。これは以下の式で表されます。

$$
S = \sum\limits_{i=1}^{n} \biggl[y_i - (ax_i + b)\biggr]^2
$$

この合計 $${S}$$ を最小にする $${a}$$ と $${b}$$ を見つけることが目標です。$${a}$$ と $${b}$$ に関する2つの方程式を導出して解くことで最適な直線のパラメータが求まります。

実際にやってみましょう。

公式の導出

線形回帰における傾き$${a}$$と切片$${b}$$の公式を導出するためには、最小二乗法の誤差関数を$${a}$$と$${b}$$に関して偏微分し、それらを0に等しいと置いて解く必要があります。

まず、誤差の二乗の合計$${S}$$を傾き$${a}$$で偏微分します。つまり、$${S}$$を$${a}$$だけの関数としたときの$${a}$$による$${S}$$の変化率です。

$$
\begin{aligned}
\dfrac{\partial S}{\partial a} &= \dfrac{\partial}{\partial a}\sum\limits_{i=1}^{n} \biggl[y_i - (ax_i + b)\biggr]^2 \\
&= \sum\limits_{i=1}^{n} 2\biggl[y_i - (ax_i + b) \biggr](-x_i) \\
&= -2 \sum\limits_{i=1}^{n} x_i(y_i - ax_i - b)
\end{aligned}
$$

$${S}$$は$${a}$$の２次式なので、この変化率$${\frac{\partial S}{\partial a} }$$が0になるところで最小値をとります。よって、次の方程式を解くことになります。

$$
\sum_{i=1}^{n} x_i(y_i - ax_i - b) = 0
$$

次に、誤差の二乗の合計$${S}$$を傾き$${b}$$で偏微分します。これは$${S}$$を$${b}$$だけの関数としたときの$${b}$$による$${S}$$の変化率です。

$$
\begin{aligned}
\dfrac{\partial S}{\partial b} &= \dfrac{\partial}{\partial b}\sum\limits_{i=1}^{n} \biggl[y_i - (ax_i + b)\biggr]^2 \\
&= \sum\limits_{i=1}^{n} 2\biggl[y_i - (ax_i + b) \biggr](-1) \\
&= -2 \sum\limits_{i=1}^{n} (y_i - ax_i - b)
\end{aligned}
$$

$${S}$$は$${b}$$の２次式なので、この変化率$${\frac{\partial S}{\partial b}}$$が0になるところで最小値をとります。よって、次の方程式を解くことになります。

$$
\sum_{i=1}^{n} (y_i - ax_i - b) = 0
$$

以上より、次の2つの方程式を解くことで、誤差の二乗の合計$${S}$$を最小にする傾き$${a}$$と切片$${b}$$の値がもとまります。

$$
\sum_{i=1}^{n} x_i(y_i - ax_i - b) = 0
$$

$$
\sum_{i=1}^{n} (y_i - ax_i - b) = 0
$$

これらの方程式を解くと、線形回帰の傾きと切片の公式が導かれます。

$$
a = \frac{n\sum (x_iy_i) - \sum x_i \sum y_i}{n\sum x_i^2 - (\sum x_i)^2}
$$

$$
b = \frac{\sum y_i - a\sum x_i}{n}
$$

まず、データ（$${x}$$と$${y}$$の値のセット）を使って、傾き$${a}$$を求めて、その傾き$${a}$$とデータを使って切片$${b}$$を求めることができます。こうして求められた傾き$${a}$$と切片$${b}$$による回帰直線は二乗誤差の合計を最小にします。

ここから複数の入力変数を扱う線形回帰へと拡張します。そのために、まずは行列を使って単純線形回帰を表現します。

行列で表現する

単純線形回帰の問題を行列の形式で表現します。

まず、データを行列$${X}$$として表現すると次のようになります。

$$
X = \begin{bmatrix}
1 & x_1 \\
1 & x_2 \\
\vdots & \vdots \\
1 & x_n
\end{bmatrix}
$$

最初の列はすべて1（切片の係数として）、2列目はデータを表しています。つまり、$${x_i}$$の値です。この$${X}$$をデザイン行列とも呼びます。

次に、$${y}$$を列ベクトルとして次のように定義します。

$$
\boldsymbol{y} = \begin{bmatrix}
y_1 \\
y_2 \\
\vdots \\
y_n
\end{bmatrix}
$$

各要素$${y_i}$$はデータからの値です。また、この$${\boldsymbol{y}}$$を応答変数ベクトルと呼んだりします。

次に、係数ベクトル$${\boldsymbol{\beta}}$$を次のように定義します。

$$
\boldsymbol{\beta} = \begin{bmatrix}
b \\
a
\end{bmatrix}
$$

最初の要素は切片 $${b}$$、2番目の要素は傾き $${a}$$ です。

これらを使うと、線形回帰の方程式は $${\boldsymbol{y} = X\boldsymbol{\beta} + \boldsymbol{\epsilon}}$$ と表されます。ここで、$${\boldsymbol{\epsilon}}$$ は誤差項です。

$$
\boldsymbol{\epsilon} = \begin{bmatrix}
\epsilon_1 \\
\epsilon_2 \\
\vdots \\
\epsilon_n
\end{bmatrix} = \boldsymbol{y} - X\boldsymbol{\beta}
= \begin{bmatrix}
y_1 - (b + ax_1) \\
y_2 - (b + ax_2) \\
\vdots \\
y_n - (b + ax_n) \\
\end{bmatrix}
$$

このようにして単純線形回帰を行列で表現しましたが、もちろん最小二乗法によって解くことができます。

誤差の二乗の合計は以下のように表現できます。

$$
S = (\boldsymbol{y} - X\boldsymbol{\beta})^\top (\boldsymbol{y} - X\boldsymbol{\beta})
$$

これを計算すると、$${S = \sum\limits_{i=1}^{n} \biggl[y_i - (ax_i + b)\biggr]^2}$$と同じなのがわかります。

この関数 $${S}$$ を最小化するには、$${S}$$ を $${\boldsymbol{\beta}}$$ に関して微分してゼロと等しいと設定します。そこで、微分をするために、まず$${S}$$を展開します。

$$
S = \boldsymbol{y}^\top \boldsymbol{y} - \boldsymbol{y}^\top X\boldsymbol{\beta} - \boldsymbol{\beta}^\top X^\top \boldsymbol{y} + \boldsymbol{\beta}^\top X^\top X\boldsymbol{\beta}
$$

この関数を $${\boldsymbol{\beta}}$$ に関して微分するとき、各項を個別に扱います。なお、ベクトルで微分するとは、ベクトルの要素ごとに偏微分したものを集めてベクトルにまとめることです。ディープラーニングで勾配などを計算するのと同じ要領です。

まず、最初の項 $${\boldsymbol{y}^\top \boldsymbol{y}}$$ は $${\boldsymbol{\beta}}$$の要素に依存しないので、微分すると 0 になります。

$${\boldsymbol{y}^\top X\boldsymbol{\beta}}$$ はスカラーです。ここで、$${\boldsymbol{y}}$$ は行ベクトル、$${X}$$ は行列、$${\boldsymbol{\beta}}$$ は列ベクトルです。この式は$${X^\top \boldsymbol{y}}$$と$${\boldsymbol{\beta}}$$の内積と見なすことができます。

ベクトル $${\boldsymbol{v}}$$ と $${\boldsymbol{u}}$$ の内積は $${\boldsymbol{v}^\top \boldsymbol{u}}$$と計算されます。また、$${\boldsymbol{u}^\top \boldsymbol{v}}$$としても同じスカラーの値になります。

よって、$${\boldsymbol{y}^\top X\boldsymbol{\beta}}$$を$${\boldsymbol{\beta}^\top X^\top \boldsymbol{y}}$$としても同じです。これを$${\boldsymbol{\beta}}$$ に関して微分すると$${X^\top \boldsymbol{y}}$$ になります。

内積の微分のルールによれば、ベクトル $${\boldsymbol{v}}$$ と $${\boldsymbol{u}}$$ の内積 $${\boldsymbol{v}^\top \boldsymbol{u}}$$ の $${\boldsymbol{v}}$$ に関する微分は $${\boldsymbol{u}}$$ です。この規則は小さいベクトルで実際に計算してみると確認できます。

同様に、次の項$${\boldsymbol{\beta}^\top (X^\top \boldsymbol{y})}$$ の $${\boldsymbol{\beta}}$$ に関する微分は $${X^\top \boldsymbol{y}}$$ になります。

最後の項$${\boldsymbol{\beta}^\top X^\top X\boldsymbol{\beta}}$$は$${\boldsymbol{\beta}^\top (X^\top X)\boldsymbol{\beta}}$$なので、$${\boldsymbol{\beta}}$$で微分すると、$${2X^\top X\boldsymbol{\beta}}$$ です。

二次形式の微分の基本ルールによると、ある対称行列 $${A}$$ に関する二次形式 $${\boldsymbol{x}^\top A\boldsymbol{x}}$$ の $${\boldsymbol{x}}$$ に関する微分は $${2A\boldsymbol{x}}$$ です。

$${\boldsymbol{\beta}^\top (X^\top X)\boldsymbol{\beta}}$$では、$${X^\top X}$$ が対称行列になっています。

以上より、$${S}$$を最小化するために次の方程式が得られます。

$$
\frac{\partial S}{\partial \boldsymbol{\beta}} = -2X^\top \boldsymbol{y} - 2X^\top X\boldsymbol{\beta} = -2X^\top (\boldsymbol{y} - X\boldsymbol{\beta}) = 0
$$

この方程式を $${\boldsymbol{\beta}}$$ について解くと、最小二乗法による解が得られます。

$$
\boldsymbol{\beta} = (X^\top X)^{-1}X^\top y
$$

以上より、単純線形回帰を行列とベクトルで表現できました。後はひたすら行列とベクトルの計算をするだけで解が求まります。

次に単純線形回帰から多変量へと拡張してみましょう。

多変量線形回帰

複数の入力変数を扱う線形回帰を多変量線形回帰と呼びます。つまり、入力変数が複数あります。

単純線形回帰から多変量へと拡張するには、デザイン行列に必要なだけ列を追加していくだけです。各列は異なる入力変数（独立変数）を表し、これまで通り最初の列は1で埋められ、これは切片の係数として使われます。

例えば、3つの入力変数 $${x_1, x_2, x_3}$$ がある場合のデザイン行列 $${X}$$ は以下のようになります。

$$
X = \begin{bmatrix}
1 & x_{11} & x_{12} & x_{13} \\
1 & x_{21} & x_{22} & x_{23} \\
\vdots & \vdots & \vdots & \vdots \\
1 & x_{n1} & x_{n2} & x_{n3}
\end{bmatrix}
$$

ここで、$${x_{ij}}$$ は $${i}$$ 番目のデータポイントにおける $${j}$$ 番目の入力変数の値です。

係数ベクトル $${\boldsymbol{\beta}}$$ は、切片を含めて入力変数の数に応じたサイズになります：

$$
\beta = \begin{bmatrix}
b \\
a_1 \\
a_2 \\
a_3
\end{bmatrix}
$$

そして、多変量線形回帰モデルは $${\boldsymbol{y} = X\beta + \boldsymbol{\epsilon}}$$ と表されます。ここで、$${\boldsymbol{\epsilon}}$$ は誤差項です。つまり、単純線形回帰も多変量線形回帰も同じ形で表現されます。

最小二乗法の解は引き続き $${\boldsymbol{\beta} = (X^TX)^{-1}X^Ty}$$ となり、これを解けば係数ベクトル $${\boldsymbol{\beta}}$$ が求められます。つまり、入力変数のそれぞれの傾き（影響力）とモデルの切片が求められ、データに対する最適な線形近似が得られます。

データ数や変数の数が増えると手計算では大変なのでscikit-learnのようなツールを使うことになります。

次回予告

次回は、scikit-learnを使って線形回帰を実践します。

お楽しみに！