六合折り紙(3)~ひねった多面体
前回・前々回に続き、折り紙6枚を組み合わせて作る「六合折り紙」を紹介していきたい。上下・左右・前後の6方向からユニットを組み合わせ、ポケットも継ぎ手もないのに、ユニット同士が互いを押さえ込み合って安定する形の作品を指している。

変な意地を張らないで普通に継ぎ手とポケットでつなげばいいじゃねえのという声もあろうが、これはこれでなかなか楽しいのである。基本的な形をちょっとアレンジするだけで、いろいろな形を作れる点もよい。
たとえば、デヴィッド・ミッチェル氏の斜方立方八面体は、六合構造の代表的なものといえる作品であり、シンプルなだけにちょっとひねるといろいろな作品を作り出せる。たとえば前川淳氏の「ひねり立方体」は、斜方立方八面体の正方形部分を、正三角形2枚に置き換えて、全体をひねった形に相当する。

ひねりの角度を変えて何かできないかなと思い、作ってみたら思ったよりうまく行ったのがこれ。正方形と直角二等辺三角形だけでできているが、全体として柔らかな印象の立体だ。

いい名前がほしいなと思って考えたが思い浮かばない。作った時にふと空を見たら月が綺麗だったので、「秋月」とでもしておこう(適当)。
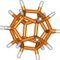
この手のひねりが効いた多面体というのは例が少ないが、化学の世界ではちょっと面白いものが知られている。藤田誠教授の研究に現れた、「拡張ゴールドバーグ多面体」というものがそれだ。正方形と正三角形でできているが、全体にひねりがあり、化学用語で言えばキラリティのある立体ということになる。

これもなんとか六合構造で作れないかなと試行錯誤しているうち、できたのが上図右の折り方だ。できてみればごくシンプルであった。
写真を見れば分かる通り、ちょっと角のまとまりが悪くごわごわしている。実はこの立体、正確には「多面体」とはいえない。先ほどは「正三角形」「正方形」と書いてしまったが、実際にはこれらの面は平面に収まっておらず、曲がっているのだ。
それでちょっと納まりが悪い出来上がりなのだが、多少のひずみは吸収してそれっぽく仕上げられるところが、折り紙のよさというものかなと思っている。