六合折り紙(2)~斜方立方八面体のバリエーション
前回、6枚の折り紙を前後・左右・上下方向から組み合わせて作る作品を、「六合」と名付けることにした話を書いた。今回はその続き。
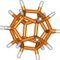
デヴィッド・ミッチェル氏の斜方立方八面体は、既存の六合構造の作品でも代表的かつ基本的なものといえそうだ。正方形の9等分からスタートして、無駄なく立体が出来上がっている。

ということで、このアレンジから始めてみることにしよう。元作品は3等分だが、この比率を変えてやるだけで、ちょっと表情の違う作品になる。

ならば中央を広くして、正三角形の面が小さいやつも作ってみるか……と思ったら、驚いたことにこれが全くまとまらず、どう頑張ってもバラけてしまう。写真のものは、業を煮やして糊付けしてしまった。

どうも六合構造においては、凹んだ面が重要であり、ここで全体を押さえ込んで安定した構造になるようだ。上のように凹みが小さいと、押さえが効かずバラけてしまうらしい。やはり折り紙作品としては、糊付けなしでまとまるものが理想であるので、これはボツである。
その後もいろいろ作ってみたが、きちっとまとまるものと、どうにもまとまらないものがある。凹みが小さいものは厳しいのは確かだが、事前予測は難しい。まあこのへんが六合構造の魅力である、ということにしておこう。
辺の比率を変えるだけでは、さすがに気が利かない。別の立体も作ってみるかということで、斜方切頂立方八面体というやつを作ってみることにする。凹んだ面が正三角形から正六角形に、中央の面が正方形から正八角形になるのでちょっと難しいが、なんとなくこれで行けるかな、と折ってみたらうまく行った。

隅の余計な部分は、折り込むなり切り落とすなりご自由に。
凹みがこれくらいの深さと大きさであれば、まあまあ形にまとまるようだ。26もの面がある立体が6枚の紙で折り上がること、紙の効率が高くすっきりまとまるので、お気に入りである。上の2例はオリジナルでございとはとてもいえないが、これくらいなら自分の作品ですと言ってもまあよかろうと思う。
ということで、また次回に続く。