
【電験三種】合格に必要な数学知識
こんにちは!建職バンクです。
建職バンクのコラムではいろいろな資格について取り上げていますが、中でも需要の高い資格が電気主任技術者です。
そして電験三種の令和4年度の試験は、8月21日(日)に行われます。あと1ヶ月ほどですが、このコラムを読んでいる方の中に受験される方もいらっしゃるのではないでしょうか。
そこで今回は、電験三種に合格するために必要な数学の知識について取り上げます。
電験三種における数学の重要性

電験三種は「理論」「電気」「機械」「法規」の4つの科目から構成されており、すべての科目において6割近く正解しなければなりません。
そして、試験科目別の計算問題の割合は以下のようになっています。
理論:8割
電力:3割
機械:5割
法規:2割
つまりすべての科目において「数学知識」が求められることになるため、しっかりと対策する必要があるでしょう。
具体的に、どの程度のレベルの知識が必要となるのかを見ていきましょう。
電験三種合格に必要な数学のレベル

電験三種に合格するために必要な数学のレベルは中学から高校レベルです。ほとんどの問題が「中学・高校数学レベルの知識と計算能力」+「電気の知識」で解答できるようなものになっています。
中学数学とはいってもなかなか範囲が広いので、その中でも必要な数学の分野をご紹介します。
① 繁分数
繁分数は分母・分子どちらかが、あるいはどちらもが分数になっている分数のことで、数学の基本中の基本といえます。
繁分数とは、例えば以下のようなものを指します。

電験三種において特に、電気回路の合成抵抗の計算では「分数の計算」が、電気の計算では「繁分数」が頻出です。
② 平方根と指数

平方根や指数の計算は、電気回路の交流の問題やインピーダンスの計算問題を解くために必要な数学知識です。
三平方の定理は頻出ですが、これはインピーダンスや電圧・電流の大きさを求めるような計算問題に使用することが多いためです。
③ 連立方程式
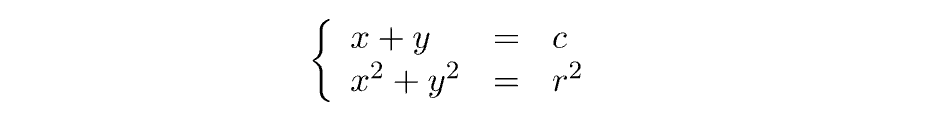
電気回路の計算で使用するキルヒホッフの法則の問題では、連立方程式を説くことが要求されます。
この計算方法とキルヒホッフの第1法則、第2法則を使用すれば解答できるような問題が多いです。
④ 三角比と三角関数
以下のような三角関数は、電気の交流計算問題でよく使用します。
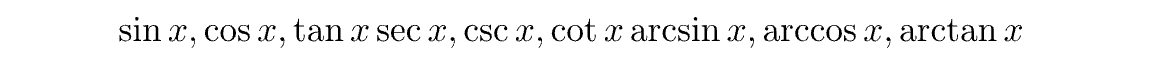
三角比や三角関数は高校数学で習う内容となっていますが、基礎的なものは中学数学で応用が可能です。
⑤ ベクトル
電験3種の試験問題では、正弦波交流の位相や各種の電気力などを計算する際にベクトルの知識と計算方法が必須になります。

⑥ 複素数
複素数は、実数の組<a,b>と虚数i=√-1を用いてa+biと示される数のことを指します。
電気工学分野では複素数により、電圧V,電流I,インピーダンスZを表現する方法のことを「記号法」といいますが、この記号法による計算において複素数の知識が必要です。
⑦ 対数、最大定理、最小定理
対数の中でも常用対数は、増幅回路の利得計算で頻出します。
最大定理、最小定理は、電気回路が最大電力を得るときの条件の計算の際に必要となります。
まとめ
電験三種に合格するために必要な数学知識は以上になります。
試験において計算問題を正確に解答する重要性は非常に高いので、しっかりと対策して試験に臨めると良いですね。
本コラムでは、電験三種などの資格合格に向けた特集から、資格を活かした年収アップ方法まで、建設業界に関わるお役立ち情報をご紹介しています。
転職サイト「建職バンク」では幅広く求人を取り扱っていますので、興味がある方はぜひこちらから求人を検索してみてください😊
