
【GARCHモデルによる特定💖】「The Effects of Japanese Foreign Exchange Intervention: GARCH Estimation and Change Point Detection」:先行研究解説 No.8 2023/09/22
Introduction:卒業論文は早めに仕上げたい💛
私もいよいよ卒業論文の執筆に
取りかかる時期がやって参りました👍
何事もアウトプット前提のインプットが
大事であると、noteで毎日発信してきました
これは、どのような内容で
あっても当てはまります👍
論文を一概に読んでも
記憶に残っていなかったり
大切な観点を忘れてしまっていたりしたら
卒業論文の進捗は滞ってしまうと思います
だからこそ、この「note」をフル活用して
卒業論文を1%でも
完成に向けて進めていきたいと思います
私の卒論執筆への軌跡を
どうぞご愛読ください📖
今回の参考文献🔥
今回、読み進めていく論文は
こちらのURLになります👍
『The Effects of Japanese Foreign Exchange Intervention: GARCH Estimation and Change Point Detection』
Eric Hillebrand Gunther Schnabl Discussion
Paper No.6 October 2003
読み終えた先行研究📚
『日本の為替介入の分析』 伊藤隆敏・著
経済研究 Vol.54 No.2 Apr. 2003
『Effects of the Bank of Japan’s intervention on yen/dollar exchange rate volatility』21 November 2004
Toshiaki Watanabe (a), Kimie Harada(b)
前回のお復習い🔖
The Effects of Japanese Foreign Exchange Intervention: GARCH Estimation and Change Point Detection
Eric Hillebrand Department of Economics, Louisiana State University
Gunther Schnabl Department of Economics and Business Administration, Tuebingen
4.1. Specification
今回の投稿では、前回の内容も含めてGARCHモデルによる推計についてアウトプットしていきたいと思います
今一度、表2を再確認しておくことにしましょう

This leads to the following GARCH specification:
集計したデータに基づくと、これはGARCHモデルによる特定を導きます
以下に、この先行研究で取り上げられているGARCHモデル(1)~(3)式の構造を定式化します📝
$$
\\GARCH Model \\
r_t = b_0 +b_1 I_t +b_2Nikkei _t +b_3 DOW_t +\epsilon_t \cdot\cdot\cdot(1)\\ \\\epsilon_t|_{\Omega_{t-1}} \backsim N(0,h_t)\cdot\cdot\cdot(2)\\ \\h_t =\omega+\displaystyle\sum_{i=1}^q \alpha_i \epsilon_{t-i}^2 +\displaystyle\sum_{i=1}^p \beta_i h_{t-j}\\ +\gamma_1|I_t|+\gamma_2 Nikkei_t^2+\gamma_3 DOW_t^2\cdot\cdot\cdot(3)
$$
以下では、このモデルに対する説明をしていくことにします
In equation (1) rt denotes the logarithmic returns of the yen/dollar spot exchange rate (conditional mean) as plotted in the upper left panel of Figure 3.
The exchange rate is assumed to be influenced by official foreign currency transactions I.
The deviation of the exchange rate from a certain bliss point increases the probability of foreign intervention as suggested by Figure 4 and shown by Frenkel, Pierdzioch and Stadtmann (2003a).
It precedes unambiguously the exchange rate changes measured at 5 p.m. Greenwich time, as Japanese foreign exchange intervention is performed in the Japanese markets and US intervention is negligible.
GARCHモデルを構成する式 (1) のrtは、図3の左上のパネルにプロットされている円/ドルのスポット為替レート (条件付き平均) の対数リターンを示しています

なお、為替レートは公式の外貨取引(介入額) Iの影響を受けると想定しています
また、図4でも、Frenkel、Pierdzioch、Stadtmann(2003a)らによって示されているように、為替レートが特定の至高点(bliss point)から乖離すると、外国介入の可能性が高まることがわかります📝
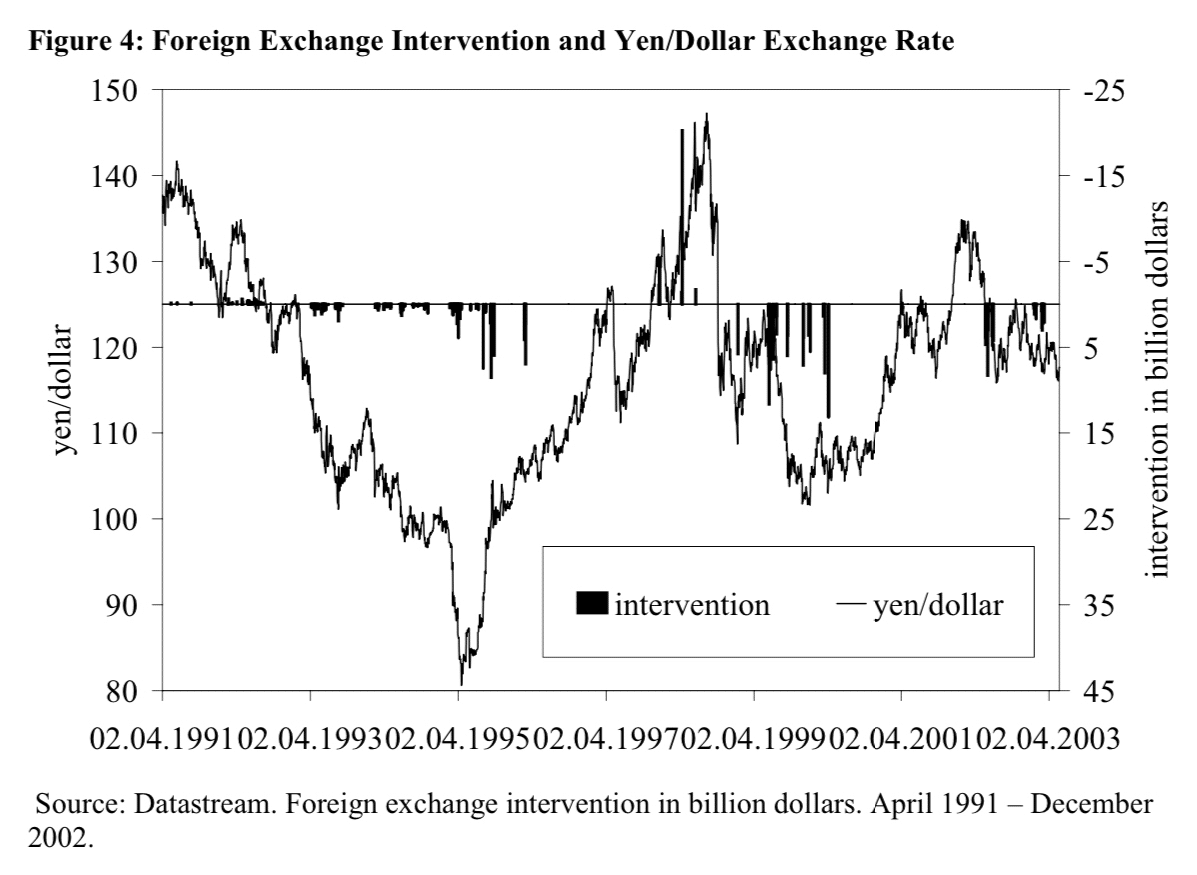
介入額を示すItは、日本の為替介入は日本の市場で行われ、米国の介入はごくわずかであるため、グリニッジ時間における午後5時に測定された為替レートの変化を明確に先行しているのです
As proposed by Bonser-Neal and Tanner (1996) we include the daily returns of Japanese and US stock markets—Nikkei 300 and DOW Jones Industrial—as exogenous variables to control for the impact of disturbances in other asset markets.
We do not include any dummies for the announcement of interest rate changes, since prior estimations with dummies did not yield any significant results.
In contrast to Dominguez (1998) and Baillie and Osterberg (1997) we do not include dummy variables for the day of the week and holidays for the sake of brevity.
この先行研究では、Bonser-NealとTanner(1996)が提案したように、他の資産市場における混乱の影響を制御するための外生変数として、日本と米国の株式市場 (日経300とDOWジョーンズ工業)の日々のリターンを含めまています👍
ただし、ダミーを使用した事前の推計では有意な結果が得られなかったため、金利変更の発表にはダミーを含めていません
Dominguez(1998)およびBaillieおよびOsterberg(1997)とは対照的に、簡潔にするために、曜日と休日のダミー変数は含めていません📝
In equation (2) the disturbances εt are modelled as normally distributed conditional on the information set Ωt-1 available at time t-1, with zero mean and variance ht.
Equation (3) models the volatility of the yen/dollar exchange rate as plotted in the lower left panel of Figure 3.
The variance ht depends on past disturbances εt-i, the lagged variance ht-j, the absolute official foreign currency intervention |It|, and the volatility in the Japanese and US share markets defined as the squares of daily returns— Nikkei_t^2 and DOW_t^2.
式(2)における、誤差項εtは、時間t-1で利用可能な情報集合 Ωt-1 を条件として正規分布としてモデル化され、平均と分散はゼロであるとします
続いて、式(3)は、図3の左下のパネルにプロットされた円/ドル為替レートのボラティリティをモデル化したものです

分散 ht は、過去の誤差項ε_{t-i}、ラグの分散h_{t-j}、公式外貨介入額の絶対値 |I_t| に依存します
また、および日次リターンの2乗として定義される日本と米国の株式市場のボラティリティ(NIKKET^2 と DOWt^2の項)もモデルに組み込んでいることを確認しておきましょう
本日の解説は、ここまでとします
このような歴史や先行研究をしっかり理解した上で、卒業論文執筆に取り組んでいきたいです
今回、私が卒業論文執筆において取り上げる
24年ぶりの「円安是正」介入は本当にレアな経済政策ということを再認識できたような気がします💖
私の研究テーマについて🔖
私は「為替介入の実証分析」をテーマに
卒業論文を執筆しようと考えています📝
日本経済を考えたときに、為替レートによって
貿易取引や経常収支が変化したり
株や証券、債権といった金融資産の収益率が
変化したりと日本経済と為替レートとは
切っても切れない縁があるのです💝
(円💴だけに・・・)
経済ショックによって
為替レートが変化すると
その影響は私たちの生活に大きく影響します
だからこそ、為替レートの安定性を
担保するような為替介入はマクロ経済政策に
おいても非常に重要な意義を持っていると
推測しています
決して学部生が楽して執筆できる
簡単なテーマを選択しているわけでは無いと信じています
ただ、この卒業論文をやり切ることが
私の学生生活の集大成となることは事実なので
最後までコツコツと取り組んで参ります🔥
本日の解説は、以上とします📝
今後も経済学理論集ならびに
社会課題に対する経済学的視点による説明など
有意義な内容を発信できるように
努めてまいりますので
今後とも宜しくお願いします🥺
マガジンのご紹介🔔
こちらのマガジンにて
卒業論文執筆への軌跡
エッセンシャル経済学理論集、ならびに
【国際経済学🌏】の基礎理論をまとめています
今後、さらにコンテンツを拡充できるように努めて参りますので何卒よろしくお願い申し上げます📚
最後までご愛読いただき誠に有難うございました!
あくまで、私の見解や思ったことを
まとめさせていただいてますが
その点に関しまして、ご了承ください🙏
この投稿をみてくださった方が
ほんの小さな事でも学びがあった!
考え方の引き出しが増えた!
読書から学べることが多い!
などなど、プラスの収穫があったのであれば
大変嬉しく思いますし、投稿作成の冥利に尽きます!!
お気軽にコメント、いいね「スキ」💖
そして、お差し支えなければ
フォロー&シェアをお願いしたいです👍
今後とも何卒よろしくお願いいたします!
