見出し画像

Excelと多倍長整数の四則演算

Uncle+K

はじめに

Excelは大きな数の計算が苦手です。
表計算アプリなのに・・・。
標準スタイルで表示すると12桁の数字「 100000000000 」が「 1E+11 」と表示されますし、桁区切りスタイルで表示しても、16桁以上だと下の桁の表示が「 0 」になります。

Excelの数字表示

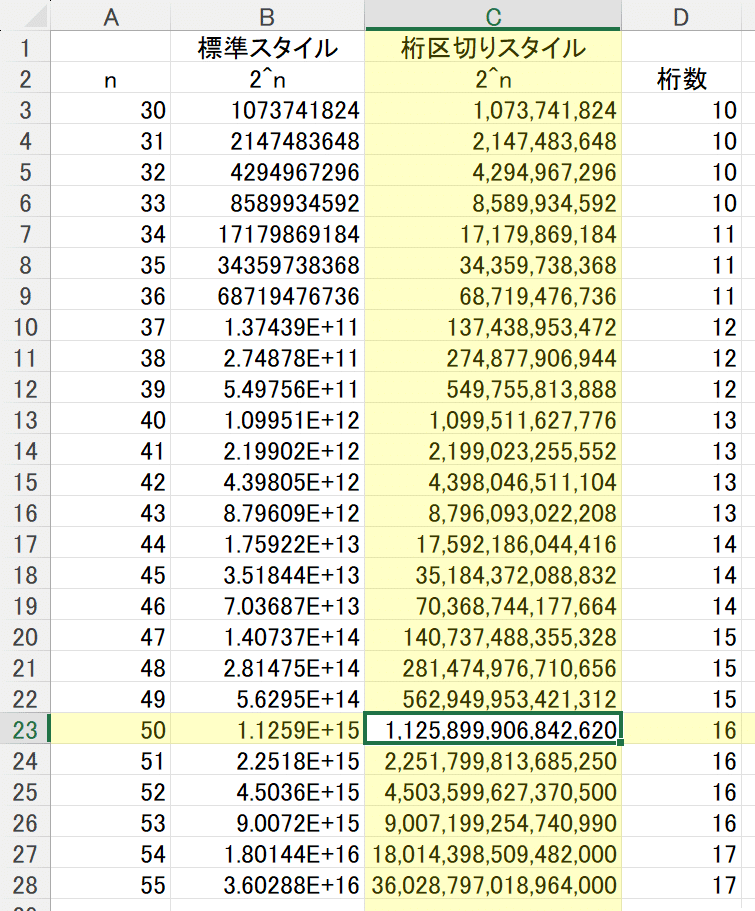
ちなみに、Windowsの計算機やiPhoneの計算機で２の100乗(31桁)を計算してもちゃんと表示してくれます。

Windows11の計算機アプリ

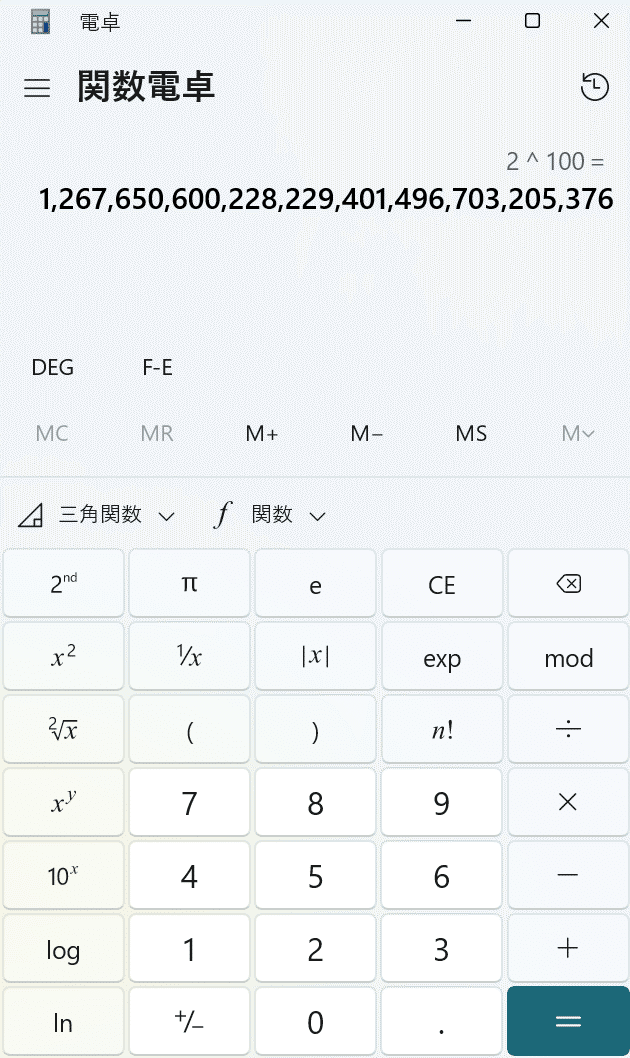
ちなみに、VBAであればLongLong型の整数(-9,223,372,036,854,775,808 から 9,223,372,036,854,775,807)が使えますが、高々19桁です。
改めて感じますが、Excelは大きな数が苦手です。
残念なことです。

「大きな数を扱いたければPythonでも使えばいいじゃないか！」と言いたい方もいらっしゃるかと思います。
そうですね。そう思います。Pythonは素晴らしいです。なんと桁数制限ないのですから！
そんなPythonがExcelに組み込まれると聞いて、期待したわけですよ。
あのザコセルくんが桁数の壁を打ち破るのか！？と。
そして失望したわけですよ。変わってないじゃないかと・・・。

Excelに捧げる歌

Excel
それはいつも儚い
一つのExcelは一瞬のうちにぶっ壊れる運命を自ら持っている
それでも人々はExcelに挑む
限りあるリソースとロマンをいつも追い続ける
それが人間Excelドカタなのである
次のExcelゴミを作るのは、あなたかもしれない。

でもなんとかしたい！

そんな制限のあるExcelですが、それでも便利なツールであるのには変わりありません。ならばせめて四則演算だけでもなんとかならないかと思っているときにこんな記事を見つけました。

３年前のQiitaの記事ですね。
筆者さん(square1001さん)は当時高校３年生とのことで、今は大学生ぐらいでしょうか。
末恐ろしいですね。私が高校生のころはBasicMagazine見ながら打ったコードが動かなくて「SyntaxErrorってなんですか！？」とか叫んでましたけれどね・・・。
ともかく、この記事に感銘を受けて、「Excelでもできるんじゃね？」と思ったわけです。

第１章　下準備

文字列数と配列数

さて、ここからが本編です。
まず最初に「文字列数」と「配列数」というものを作ります。
Excelでは16桁以上の数字がまともに表示されないわけですが、Excelの１つのセルに入る文字列は結構あります。
ググってみると32,767文字入るそうです。
試したことはないですし、試そうとも思わないですが、そこそこ入るということは信じておきましょう。
つまり、文字列として入力すれば大きな数字も表示できるというわけですが、セル書式をいちいち「文字列スタイル」に変更するのも面倒くさいので、次のようにしてみます。

  • p12345678901234567890

  • n98765432109876543210

先頭の「 p 」はポジティブ(positive)、「 n 」はネガティブ(negative)です。
つまり「 ＋ 」(プラス)と「 ー 」(マイナス)を表しています。
こうすれば文字列として扱われるので、セル書式を変更せずに、大きな数を入力することができます。
これを「文字列数」(Cn：Character numbers)と呼ぶことにします。

次に、「配列数」(An：Array numbers)です。
square1001さんの記事を読まれた方は、理解できると思いますが、大きな数を計算するためには、一桁ずつ数字をばらす必要があります。
そこで文字列数を次の様にばらします。

  • p12345　⇒　{ 5, 4, 3, 2, 1 }

左右が逆になっているのは、その方が扱いやすいからですね。
配列数はあくまで関数内で使用する数なので、符号情報は持たせていません。これは後ほど四則演算の関数にて説明します。
まずは、文字列数を配列数に変換する関数です。

文字列数⇒配列数

FuncName : _CnToAn

Discription : 文字列数を配列数に変換する。

Argments : cn

Function definition :
=LET(
	_cn, _CnAbs(cn), 
	_s, SORT(SEQUENCE(, LEN(_cn)), , -1, TRUE), 
	VALUE(MID(_cn, _s, 1))
)

簡単に解説します。
先に補足として、上のコードは、Excel Labsの表示をコード風に表示しています。
実際には、

=LAMBDA(cn,LET(_cn, _CnAbs(cn), _s, SORT(SEQUENCE(, LEN(_cn)), , -1, TRUE), VALUE(MID(_cn, _s, 1))))

という１ライナーなコードに「_CnToAn 」という名前を定義しています。
このあたりはLAMBDA関数の仕様を理解していないと難しいと思いますが、それはもっと詳しく丁寧に解説されている方がいらっしゃいますので、そちらをどうぞ。
ではLET関数の中身を見ていきます。
まず１行目

_cn, _CnAbs(cn),

これは、「 _cn 」という変数に、引数「 cn 」の絶対値を入れています。
「_CnAbs」という関数で、文字列数の先頭についている「 p 」「 n 」などの符号を取り除いています。
実際にやっていることは、例えば引数が「 p987 」とすると、数字以外を除去して「 987 」という文字列を作っています。
実際はもう少し複雑なことをしていますが、いまのところこの理解で問題ありません。

２行目は配列を作っています。

_s, SORT( SEQUENCE( , LEN(_cn) ), , -1, TRUE ),

１行目で _cn = "987" となったので、

  • LEN( _cn ) ⇒ LEN( "987" ) ⇒ 3

となり、

  • SEQUENCE( , LEN(_cn) ) ⇒ SEQUENCE( , 3) ⇒ { 1, 2, 3 }

となります。
SEQUENCE関数の第１引数(行数)は省略しているので、行数は１、列数が３の配列ができます。第３引数と第４引数も省略しているので、初期値１、増加分１として配列が作られます。
それをSORT関数で降順に並べ替えています。
つまり、

  • SORT( { 1, 2, 3 } , , -1, TRUE ) ⇒ { 3, 2, 1 }

となります。
３行目が返り値です。

VALUE( MID( _cn, _s, 1 ) )

MID関数は文字列から指定した長さの文字を抜き出す関数です。
この場合、_cn = "987" から文字を抜き出すわけですが、第２引数が配列_s = { 3, 2, 1 } になっているのが難しいですね。

  • MID( _cn, _s, 1 ) ⇒ MID( "987", { 3, 2, 1 }, 1 )

この引数に配列を渡すのは、スピルならではの仕様です。
慣れないと意味不明な表記ですが、配列の中を１つずつ順番に処理していくだけなんですね。
つまり、

  • MID( "987", 3, 1 ) ⇒ "7"

  • MID( "987", 2, 1 ) ⇒ "8"

  • MID( "987", 1, 1 ) ⇒ ”9"

と、順番に処理を行い、{ 7, 8, 9 } という配列を返すというわけです。
最後に、VALUE関数で文字から数字に変換して返しています。
つまり、VALUE( { 7, 8, 9 } ) = { 7, 8, 9 } です。
一見無意味に見えますが、Excelは文字列を数字を区別しているので、こういう処理をしておかないと後々意味不明のエラーが出てしまいます。
なので大事なのです。
この値がLET関数の返り値となり、さらに_CnToAn関数の返り値となります。
実際に動かしてみたのがこちら、

_CnToAn関数

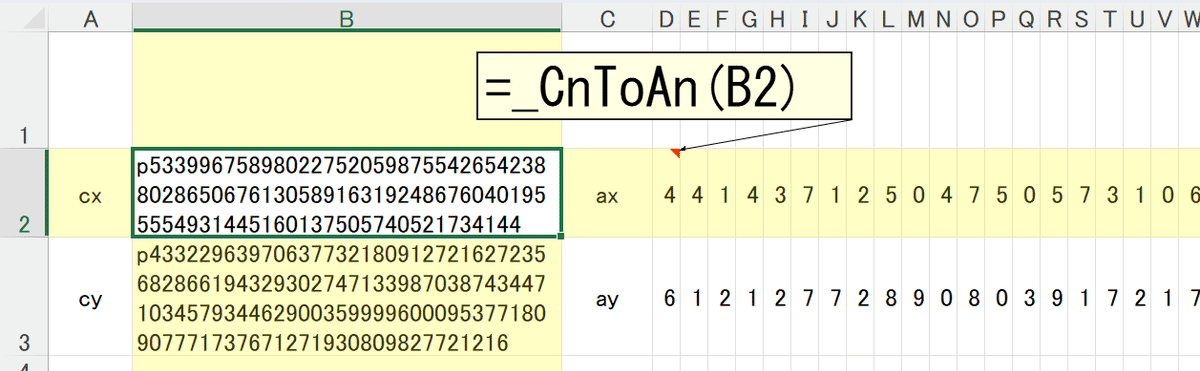
cx：(B2)が96桁、cy：(B3)が128桁あります。
なので、右側はもっとずっと続いています。
配列数は計算のしやすさを考慮し、左側が１桁目になっていますので、文字列数とは鏡合わせの状態ですね。

配列数⇒文字列数

さて、配列数はあくまで計算のために使うもので、最終的には文字列数に戻して表示しないといけないので、逆関数が必要です。
つまり、_AnToCn関数ですね。

FuncName : _AnToCn

Discription : 配列数を文字列数に変換する。

Argments : an

Function definition :
=CONCAT(SORTBY(an, SEQUENCE(, COLUMNS(an)), -1))

中身から見ていきましょう。
COLUMNS関数は、配列の列数を数える関数です。
例えば、an = { 9, 8, 7 } という配列だったら、

  • COLUMNS( { 9, 8, 7 } ) ⇒ 3

となります。
それをSEQUENCE関数で囲っています。つまり３列の配列を作っています。
第１引数が省略されていますので、行数は１。
また、第３引数と第４引数も省略されているので、初期値１、増加１です。
つまり、

  • SEQUENCE( , 3 ) ⇒ { 1, 2, 3 }

となります。
これをつかって、SORTBY関数で「an」を反転させています。

  • SORTBY( { 9, 8, 7 }, { 1, 2, 3 }, -1 ) ⇒ { 7, 8, 9 }

これで反転が終わったので、CONCAT関数で１つの文字列に結合しています。

  • CONCAT( { 9, 8, 7, } ) ⇒ "789"

符号と大小関係

これで下準備ができたかと思ったら、まだまだ足りないものがありました。
それを理解してもらうために、先に文字列数の加算関数のコードを見てもらいましょう。

FuncName : CnAdd

Discription : 文字列数の加算。

Argments : cx, cy

Function definition :
=LET(
    _cc, _CnCmp(cx, cy),
    _cx, IF(_cc >= 0, cx, cy),
    _cy, IF(_cc >= 0, cy, cx),
    _sx, _GetCnSign(_cx),
    _sy, _GetCnSign(_cy),
    _ax, _CnToAn(_cx),
    _ay, _CnToAn(_cy) * (_sx * _sy),
    _az, _AnAdd(_ax, _ay),
    IF(_sx > 0, "p", "n") & _AnToCn(_az)
)

未説明の関数がいくつかあります。
列挙してみましょう。

  1. _CnCmp

  2. _GetCnSign

  3. _AnAdd

この３つですね。
３つ目の「 _AnAdd 」は、実際に加算をしている部分なので後ほど詳しく説明します。

「_CnCmp」は、文字列数の絶対値の大小関係を調べる関数です。

FuncName : _CnCmp

Discription : 文字列数の絶対値大小比較。cx>cy：1、cx=cy：0、cx<cy：-1

Argments : cx, cy

Function definition :
=LET(
    _x, _CnAbs(cx),
    _y, _CnAbs(cy),
    _d, LEN(_x) - LEN(_y),
    IFS(_d > 0, 1, _d < 0, -1, _x > _y, 1, _x < _y, -1, TRUE, 0)
)

「_CnAbs」は文字列数から符号を取り除いています。
そして、３行目のLEN関数で、それぞれの文字列の長さをはかります。
４行目が大小比較です。
「cx」が大きい場合に「1」、「cy」が大きい場合は「-1」、同じ場合は「0」を返します。

次の関数は「_GetCnSign」ですね。
これは文字列数についている符号を「1」か「-1」に変換しています。

FuncName : _GetCnSign

Discription : 文字列数の符号を取得する。

Argments : cn

Function definition :
=LET(_s, LEFT(cn, 1), IF(_s = "n", -1, 1))

実際は先頭の文字が「n」の時だけ「-1」にしています。

これでようやく、下準備がようやく終わりました。
ちょっと振り返りましょう。

  1. _CnToAn( cn )：文字列数を配列数に変換する。

  2. _AnToCn( an )：配列数を文字列数に変換する。

  3. _CnCmp( cx, cy )：文字列数の絶対値大小比較。

  4. _GetCnSign( cn )：文字列数の符号を取得する。

第２章　加算・減算

文字列数の加算関数

改めて文字列数の加算関数を見てみます。

FuncName : CnAdd

Discription : 文字列数の加算。

Argments : cx, cy

Function definition :
=LET(
    _cc, _CnCmp(cx, cy),
    _cx, IF(_cc >= 0, cx, cy),
    _cy, IF(_cc >= 0, cy, cx),
    _sx, _GetCnSign(_cx),
    _sy, _GetCnSign(_cy),
    _ax, _CnToAn(_cx),
    _ay, _CnToAn(_cy) * (_sx * _sy),
    _az, _AnAdd(_ax, _ay),
    IF(_sx > 0, "p", "n") & _AnToCn(_az)
)

  1. 文字列数の絶対値を比較し、大きい方を「_cx」、小さい方を「_cy」に代入（１～３行目）

  2. それぞれの符号を取得（４,５行目）

  3. 文字列数を配列数に変換（６,７行目）

    1. その際、双方の符号が逆の場合、引き算になるように７行目で符号をかける。

  4. ８行目で配列数の加算

  5. ９行目は、配列数を文字列数に変換し、符号を頭につける

こうなっています。
では、ここから配列数の加算を見ていきます。

配列数の加算

FuncName : _AnAdd

Discription : 配列数の加算。正の整数のみを対象とする。

Argments : ax, ay

Function definition :
=LET(
    _x, ax,
    _y, ay,
    _lx, COLUMNS(_x),
    _ly, COLUMNS(_y),
    _lz, MAX(_lx, _ly),
    _Nn, LAMBDA(_arr, _len, _no, IF(_no <= _len, INDEX(_arr, 1, _no), 0)),
    _Xn, LAMBDA(_no, _Nn(_x, _lx, _no)),
    _Yn, LAMBDA(_no, _Nn(_y, _ly, _no)),
    _z, MAKEARRAY(1, _lz, LAMBDA(_r, _c, _Xn(_c) + _Yn(_c))),
    _AnCarryAndFix(_z)
)

まずは構成を見ていきましょう。

  1. １～５行目は下準備です。１,２行目は引数の値を変数に突っ込んでいるだけなので、特に意味はありません。３,４行目で配列の長さを測って、５行目で大きいほうほ値を取得しています。

  2. ６～８行目はヘルパー関数です。配列の任意の場所の値をひろうにはINDEX関数を使うのですが、配列外の値を指定されたとき、０を返すようにしています。このようにLET関数内で関数内関数を作れるのはとても便利ですね。

  3. ９行目のMAKEARRAY関数が加算の本体です。_x、_yそれぞれから１桁ずつ数字を取り出し、足し算して新たな配列に突っ込みます。

  4. 10行目は後処理です。いわゆる繰り上がりの処理をしています。

配列数計算のキモは、最後の「_AnCarryAndFix」関数です。
こいつはなかなか難しいことをしています。

繰り上がり処理

FuncName : _AnCarryAndFix

Discription : 配列数の繰上げ（繰下げ）処理を行う。

Argments : an

Function definition :
=LET(
    _an, an,
    _l, COLUMNS(_an),
    _a, HSTACK(0, _an, 0, 0),
    _s, SEQUENCE(, _l),
    _r1, REDUCE(
        _a,
        _s,
        LAMBDA(_a, _s,
            LET(
                _n1, INDEX(_a, 1, _s + 1),
                _n2, INDEX(_a, 1, _s + 2),
                _c, IFS(_n1 >= 10, INT(_n1 / 10), _n1 < 0, -1 * INT((9 - _n1) / 10), TRUE, 0),
                HSTACK(TAKE(_a, , _s), _n1 - _c * 10, _n2 + _c, DROP(_a, , _s + 2))
            )
        )
    ),
    _r2, DROP(_r1, , 1),
    _l2, COLUMNS(_r2),
    _rr2, SORTBY(_r2, SEQUENCE(, _l2), -1),
    _l3, _l2 - IFERROR(MATCH(0, 0 / (_rr2 <> 0), 0), _l2) + 1,
    _r3, TAKE(_r2, , _l3),
    _r4, _CnToAn(INDEX(_r3, 1, _l3)),
    IF(_l3 = 1, _r4, HSTACK(TAKE(_r3, , _l3 - 1), _r4))
)

難しい・・・。とりあえず順をおって説明します。

  1. １～４行目は下準備です。

    1. ２行目は配列数の長さを取っています。

    2. ３行目は初期値です。繰り上がり処理の際に例外処理を無くすための工夫をしています。

    3. ４行目はループカウント用の配列です。

  2. ５行目が繰り上がり処理です。REDUME関数を使ってループします。

    1. ６行目が初期値、７行目がループ用配列です。

    2. ８行目のLAMBDA関数が本体です。

      1. 最初の「_a」「_s」は上の「_a」「_s」が代入されます。

      2. 次のLET関数の返り値がまた「_a」に代入され、「_s」の配列の長さ分ループする仕組みです。

        1. 配列から当番と次番の数をとってきます。なぜ当番が＋１されているかというと、３行目で初期値を作るときに、ダミーの０を先頭にくっつけているからですね。これにより次々行のコードに例外処理を入れなくてすんで、見やすくなります。

        2. 「_c」には繰り上がり数を入れます。このとき同時に繰り下がり判定もしています。つまり、０以下の数字が配列に入っていた場合、次の桁を繰り下げるのですね。

        3. そして最後に新しい配列を作ります。これで完成。

  3. 17行目の「_r2」は後処理です。ダミーでくっつけた先頭の0を削っています。

  4. 18～21行目はおしりの０を消し込む処理です。

    1. ３行目でおしりに０を足していますので、こちらを消します。それ以外にもおしりに０が並ぶことがあるので、全部消してしまいます。

    2. 19行目の「_rr2」は「_r2」の中身を左右逆にしています。

    3. 20行目でトリッキーなのは、「 0 / (_rr2 <> 0) 」のところでしょうか。私もネットで検索して、このコードを見つけたときは「？？？」となりました。気になる方は自分で試してみるといいですよ。

    4. 上の行でおしりの０の連続数を調べて有用部分の長さがわかったので、TAKE関数で取得しています。

  5. 22,23行目はおしりの数が10以上になっている場合の後処理です。

長い！　そして難しい。もう１度作れをいわれても作れないかもしれない。
とにかくこれで加算ができました。
結果を見る前に、減算も見てみましょう。

文字列数の減算関数

FuncName : CnSub

Discription : 文字列数の減算。

Argments : cx, cy

Function definition :
=LET(
    _cc, _CnCmp(cx, cy),
    _cx, IF(_cc >= 0, cx, cy),
    _cy, IF(_cc >= 0, cy, cx),
    _sx, _GetCnSign(_cx),
    _sy, _GetCnSign(_cy),
    _ax, _CnToAn(_cx),
    _ay, _CnToAn(_cy) * (_sx * _sy * -1),
    _az, _AnAdd(_ax, _ay),
    IF(_sx * _cc >= 0, "p", "n") & _AnToCn(_az)
)

お分かりになりますでしょうか。
実は、使っている関数は、「_CnAdd」とまったく同じです。「_AnSub」という関数は無いのですね。
最初は、「_AnSub」も作ったのですが、こねくり回しているうちに、「実は同じ処理をしている」と気づいて消しました。
加算と減算は符号をどう処理するかだけの違いなのですね。ちょっと不思議。

加算・減算の出力結果

結果をみる前に、次の関数を作ったので簡単に説明します。

FuncName : RandCn

Discription : N桁のランダムな文字列数を生成する

Argments : n

Function definition :
=LET(
    _n, CEILING.MATH(n, 5),
    _r, RANDBETWEEN(10000, 99999),
    _z, REDUCE(_r, SEQUENCE(_n), LAMBDA(_a, _b, LET(_r, RANDBETWEEN(10000, 99999), _a & _r))),
    LEFT(_z, n)
)
FuncName : Tc_CnAdd

Discription : 関数の処理時間を測る

Argments : x,y

Function definition :
=LET(
	_t1, NOW(), 
	_z, CnAdd(x,y), 
	_t2, NOW(), 
	_t3, TEXT(_t2 - _t1, "s.000") & "sec", 
	HSTACK(_z,_t3)
)

これらは本題ではないので説明は省きます。では出力結果です。

CnAdd関数とCnSub関数の出力結果

計測値は200桁の計算で0.01秒となっています。
しかし、体感はもっとかかっています。まぁ、乱数もEnterキーを押すたびに再計算されているので、そっちが重いというのもあります。

ようやく加算・減算が終わりました。
次は乗算ですが、一旦ここで切りたいと思います。

ここまで読んでいただいてありがとうございました。
次回「文字列数の乗算」をお楽しみに！

追記(2025/1/19)

公開後に、「あれ？配列の足し算って、長さをそろえればエラーなしでできるんじゃね？」と思いつき、やってみたらできました。

FuncName : _AnAdd2

Discription : 配列数の加算。長さをそろえて足し算。

Argments : ax, ay

Function definition :
=LET(
    _lx, COLUMNS(ax),
    _ly, COLUMNS(ay),
    _dl, _lx - _ly,
    _x, ax,
    _y, IF(_dl = 0, ay, HSTACK(ay, SEQUENCE(, _dl, 0, 0))),
    _z, _x + _y,
    _AnCarryAndFix(_z)
)

なぜこんな簡単なことが思いつかないのか・・・。
ともかくできました。
速度を比べてみましょう。

_AnAdd関数と_AnAdd2関数の速度比べ

再計算が走るたびに秒数が変わるため、正確なことは言えませんが、1.5～2倍ほど早いようです。
コードも見やすいし、こっちに置き換えましょう。
おそらく、最も時間がかかっているのは繰り上がり処理かと思うので、そちらの高速化ができたら、また追記します。

追記２(2025/1/20)

掛け算の処理をするにあたり、上記の_AnAdd2関数だと都合が悪いことが分かったので、少々書き直しました。

FuncName : _AnAdd

Discription : 配列数の加算。長さをそろえて足し算。

Argments : ax, ay

Function definition :
=LET(
    _lx, COLUMNS(ax),
    _ly, COLUMNS(ay),
    _maxl, MAX(_lx, _ly),
    _x, EXPAND(ax, , _maxl, 0),
    _y, EXPAND(ay, , _maxl, 0),
    _z, _x + _y,
    _AnCarryAndFix(_z)
)

引数「ax」,「ay」のどちらが大きくても問題ないように、長い方に合わせてパディングするようにしました。
これら修正をしたファイルを置いておきます。

デバッグしていただけると嬉しいです。

追記３(2025/1/21)

vunuさんよりコメントをもらって、_AnCarryAndFix関数を修正しました。

FuncName : _AnCarryAndFix

Discription : 配列数の繰上げ（繰下げ）処理を行う。

Argments : an

Function definition :
=LET(
    _an, an,
    _bn, SCAN(0, _an, LAMBDA(_p, _q, INT((_p + _q) / 10))),
    _z1, HSTACK(_an, 0) - HSTACK(10 * _bn, 0) + HSTACK(0, _bn),
    _l1, COLUMNS(_z1),
    _r1, SORTBY(_z1, SEQUENCE(, _l1), -1),
    _l2, _l1 - IFERROR(MATCH(0, 0 / (_r1 <> 0), 0), _l1) + 1,
    _z2, TAKE(_z1, , _l2),
    _z3, _CnToAn(INDEX(_z2, _l2)),
    IF(_l2 = 1, _z3, HSTACK(TAKE(_z2, , _l2 - 1), _z3))
)

繰上げ処理にSCAN関数を使うことにより劇的な速度アップ！
どうなったかというと、

新_AnCarryAndFixの威力！

数字がでかすぎて見えませんが、3万桁＋３万桁が0.11秒です。
Excelのセルは最大文字数32,767だそうで、たしかにそれ以上は表示されていないようです。
（A3セルに40,000と入れてもC3セルは32,766と表示される）
最初の激重関数からすると感無量です。

新しいファイルを置いておきますので、ご自由に遊んでみてください。
（デバッグよろしくおねがいします。）

いいなと思ったら応援しよう！