
Excelと多倍長整数の四則演算の4
Excelでどこまでできるかチャレンジ!の4回目です。
回をおって、私のノートパソコンのフリーズ回数も増えてきました・・・。
今回は指数演算(べき乗)です。
第5章 指数
べき乗の方法
べき乗のアルゴリズムは、いろいろあるようなのですが、正確な名前と方法がよくわかりません。(私の勉強不足です)
検索してなんとなくわかった方式を試してみます。
愚直ループ
バイナリ法
より高速なやつ?
愚直ループ
文字通り、$${x^n}$$なら、$${n}$$回ループする方法です。
コードと計算結果がこちら。
Function Name : CnPowHo
Discription : 文字列数のベギ乗。愚直版。
Argments : cx, n
Function definition :
=LET(
_n, VALUE(_CnAbs(n)),
_sx, _GetCnSign(cx),
_sz, IF(AND(_sx = -1, ISODD(_n)), "n", "p"),
_ax, _CnToAn(cx),
_az, IF(_n > 1, _AnPowHo(_ax, _n), IF(_n = 1, _ax, 1)),
_sz & _AnToCn(_az)
)Function Name : _AnPowHo
Discription : 配列数のベギ乗。愚直版。
Argments : ax, n
Function definition :
=REDUCE(
ax, SEQUENCE(n - 1),
LAMBDA(
_a, _s,
_AnMul(_a, ax)
)
)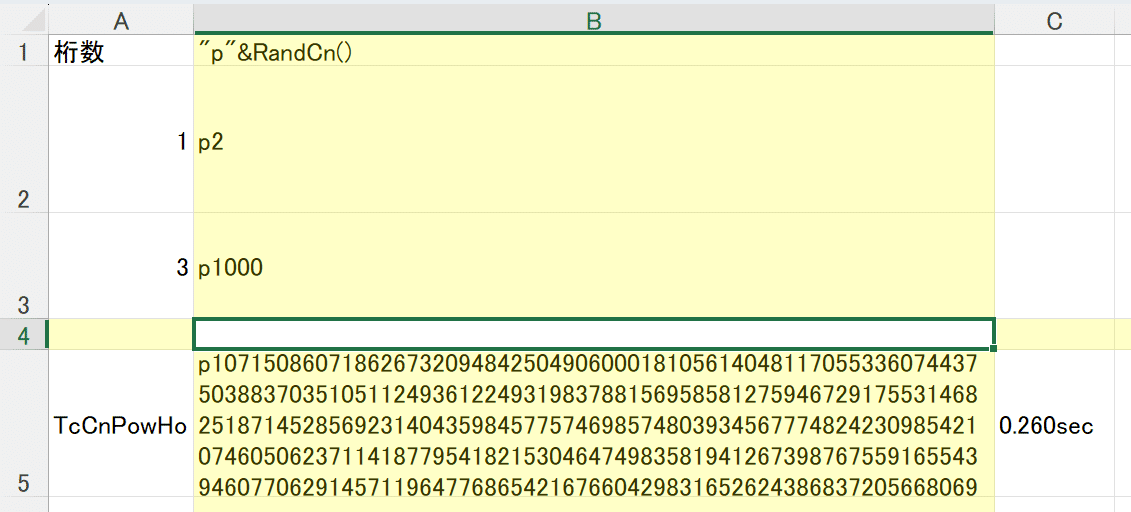
ちゃんと動きました。
_AnPowHo関数の中身は、単純なREDUCE関数でのループですので、説明もいらないかと思います。
CnPowHo関数で$${n>1}$$として2以上の場合のみ計算するようにしています。
あと、_AnPowHo関数の中に_AnMul関数というやつがいますが、これは第3章の_AnMulWc関数と_AnMulFft関数を、桁数によって使い分けている関数です。後ほど、ファイルを置いておくので、中身が気になる方は直接見てください。
バイナリ法
バイナリ法の正確な定義はわかりませんが、皆さんが言っているのはたぶんこんな感じ。
例えば$${x^n}$$を計算する場合、
$${y:=1}$$、$${z:=x}$$とおく。
$${n}$$が奇数のとき、$${y := y × z}$$をする。
$${z := z × z}$$をする
ビットシフト$${n:=n>>1}$$する。
これを、$${n = 0}$$になるまで繰り返す。
$${y}$$を返す。
例えば$${2^5}$$を考えると、
$${y=1,z=2,n=5}$$が初期値。
$${n=5}$$は奇数なので、$${y:=y×z=1×2=2}$$
$${z:=z×z=2×2=4}$$
$${n:=5>>1=2}$$
1周して、$${y=2,z=4,n=2}$$となる。
$${n=2}$$は偶数なので、$${y}$$はそのまま。
$${z:=z×z=4×4=16}$$
$${n:=2>>1=1}$$
2周して、$${y=2,z=16,n=1}$$
$${n=1}$$は奇数なので、$${y:=y×z=2×16=32}$$
$${z:=z×z=16×16=256}$$
$${n:=1>>1=0}$$
$${n=0}$$になったので終了。$${y=32}$$を返す。
こんな感じです。
最後の$${z:=z×z=16×16=256}$$は無駄ですね。条件をつけて処理しないようにしましょう。
さて、ループ内に$${y}$$と$${z}$$の2変数があるので、REDUME関数で実装するのはちとめんどうくさい・・・。
とりあえず、VSTACK関数で2変数を強引に並べてループしてみたのがこちら。
Function Name : _AnPowBi
Discription : 配列数のベギ乗。バイナリ―法
Argments : ax, n
Function definition :
=LET(
_x, ax,
_n, n,
_v, REDUCE(
VSTACK(1, _x),
SEQUENCE(1 + LOG(_n, 2), , 0),
LAMBDA(_a, _s,
LET(
_y, LET(_r, CHOOSEROWS(_a, 1), FILTER(_r, NOT(ISERROR(_r)))),
_z, LET(_r, CHOOSEROWS(_a, 2), FILTER(_r, NOT(ISERROR(_r)))),
_ns, BITRSHIFT(_n, _s),
_y2, IF(BITAND(_ns, 1), _AnMul(_y, _z), _y),
_z2, IF(_ns = 1, 0, _AnMul(_z, _z)),
VSTACK(_y2, _z2)
)
)
),
CHOOSEROWS(_v, 1)
)では、説明です。
_x、_nはそのままですね。
_v:REDUCE関数の返り値が入ります。これはVSTACK関数で並べた2行のデータになっています。{ _y2, _z2 }
REDUCE関数内
初期値:1行目に1、2行目に_xを入れています。1行目が$${y}$$、2行目が$${z}$$にあたります。
ループ配列:指数をバイナリ表示にしたときの長さです。
$${n=5}$$の場合、$${1+LOG(5,2)=1+2=3}$$なので、$${SEQUENCE(3,,0)={0,1,2}}$$となります。
_y:_aの1行目を取ってきて、エラーセルをFILTER関数で除去しています。1行目と2行目の長さが違うと、エラーが入ってしまうので苦肉の策です。
_z:_aの2行目を代入
_ns:_nをビットシフトしています。最初の_sは0なので、シフトしません。
_y2:_nsが奇数なら_yに_zを掛けます。奇数判定をBITAND関数でしているのは、なんとなくノリです。
_z2:_nsが0になったら計算終了。そうでなければ_zに_zを掛けます。
最後に_y2と_z2をVSTACK関数で並べてループします。
ループが終わったら、_vの1行目に$${y}$$の値が入っているので取り出して終わりです。
実行結果がこちら、

早いですね。
単純に20倍ぐらいの速さになっています。
しかし、愚直版CnPowHo関数が999回乗算しているのに対し、バイナリ版CnPowBi関数の乗算回数はかなり少ないはず。
実際の乗算回数はこうなると考えられる。
1000をバイナリ表記すると、「1111101000」。10桁で、1が6個。
$${z×z}$$が$${10-1=9}$$で9回、$${y×z}$$が6回、合計15回。
$${999÷15=66.6}$$なので、60倍ぐらい早くなってほしい!
このコードだと、変数周りでごちゃごちゃしているのが重そうなので、シンプル版も作ってみました。
Function Name : _AnPowB2
Discription : 配列数のベギ乗。バイナリ法改良版
Argments : ax, n
Function definition :
=REDUCE(
1,
LET(
_v1, IF(ISODD(n), 1, 2),
_v2, REDUCE(
_v1,
SEQUENCE(LOG(n, 2)),
LAMBDA(_a, _s,
LET(
_ns, BITRSHIFT(n, _s),
IF(ISODD(_ns), VSTACK(1, 0, _a), VSTACK(0, _a)))
)
),
FILTER(_v2, _v2 < 2)
),
LAMBDA(
_a, _s,
IF(_s = 0, _AnMul(_a, _a), _AnMul(_a, ax))
)
)配列側で、$${x×x}$$をするか、$${y×z}$$をするのか決めて、単純ループです。ループ回数は多くなりますが、乗算の回数は同じです。
配列を作るLET関数内を説明します。
_v1:一番最後の処理を決めます。
奇数のときは「1」で良いのですが、偶数のときは「なにもしない」のでブランクにしようかとも思ったのですが、そしたらブランクの配列ができてしまうので、適当に「2」にして最後にFILTER関数で消しています。
_v2:「$${n}$$をバイナリ表記にしたときの長さ ー 1」回ループ。
$${n}$$をビットシフトして、奇数ならVSTACK関数で頭に{1,0}をつけます。
逆に偶数なら{0}を頭につけます。
FILTER関数で「2」を消します。
これでなぜうまくいくのかは、次のように考えています。
$${n}$$に対して、奇数なら1を引く、偶数なら「2」で割る、という処理を「1」になるまで繰り返す。
例えば、$${n=6}$$の場合、
6→3→2→1
偶数を0、奇数を1に置き換える。
{6,3,2,1} → {0,1,0,1}
左右をひっくり返す。これが欲しい配列。
{0,1,0,1} → {1,0,1,0}
上記コードでは、ビットシフトを使うことで、「奇数なら1引いて2で割る」になっています。奇数と偶数の処理を1回でやっているかんじです。
このバージョン2の実行結果がこちら

1.5倍ほど早くなりました。
より高速なやつ?
検索すると「window法」や「sliding window法」「バイナリ法より乗算回数が少ない方法」などが、ヒットします。
しかし、どれもまだ理解できないので、本日はここまで。
いつか理解して、よりはやくなったら追記したいと思います。
勉強結果
今回の勉強結果はこちら
デバッグよろしくお願いします。
