見出し画像

Excelと多倍長整数の四則演算の３

Uncle+K

Excelで大きな数字の計算をしてみたい！の３回目です。
今回は割り算（除算）です。
それでは行ってみましょう。


第４章　除算

割り算の方法

毎度おなじみ、Qiitaの記事では、割り算の方法として３つ紹介されています。

  • 筆算

  • ニュートン＝ラフソンの割り算アルゴリズム

  • ゴールドシュミットの割り算アルゴリズム

では筆算からはじめましょう。

割り算の筆算

割り算は小学校３年生で習うそうです。
私は、小４のころ、小数点のある掛け算で０点を取った覚えがあります。
昔から引き算、掛け算、割り算が苦手でした。
では、足し算が得意かと言われるとそうでもない。
つまりは、四則演算すべて苦手なんですね。苦労するわけだ。
さて、では、割り算の筆算のおさらいから始めましょう。

123÷8＝15余り3

割る数(除数)が８、割られる数(被除数)が１２３。
それで、商が１５、余りが３ですね。
これをプログラムでやるのか・・・しんどい。
いろいろ試行錯誤した結果、できたコードがこちら。

Function Name : _AnDivWc

Discription : 配列数の割り算。筆算。

Argments : ax, ay

Function definition :
=LET(
    _x, ax,
    _y, ay,
    _lx, COLUMNS(_x),
    _ly, COLUMNS(_y),
    _lz, _lx - _ly + 1,
    _ys, REDUCE(
        EXPAND(_y, , _ly + 1, 0),
        SEQUENCE(8, , 2),
        LAMBDA(_a, _s, VSTACK(_a, EXPAND(_AnMulWc(_y, _s), , _ly + 1, 0)))
    ),
    _z, REDUCE(
        HSTACK("p", _x),
        SEQUENCE(_lz, , _lz, -1),
        LAMBDA(_a, _s,
            LET(
                _sx, IFERROR(DROP(_a, , _s), 0),
                _cmp, REDUCE(
                    _AnCmp(_sx, CHOOSEROWS(_ys, 1)),
                    SEQUENCE(8, , 2),
                    LAMBDA(_a, _s, VSTACK(_a, _AnCmp(_sx, CHOOSEROWS(_ys, _s))))
                ),
                _m, IFERROR(MATCH(-1, _cmp, 0), 10) - 1,
                _ym, IF(_m = 0, 0, CHOOSEROWS(_ys, _m)),
                _sym, IF(_s = 1, _ym, HSTACK(SEQUENCE(, _s - 1, 0, 0), _ym)),
                _dx, _AnAdd(DROP(_a, , 1), -1 * _sym),
                HSTACK(CONCAT(TAKE(_a, , 1), _m), _dx)
            )
        )
    ),
    _AnCarryAndFix(_CnToAn(INDEX(_z, 1, 1)))
)

かなり複雑ですね。よく動いているなこれ。
説明の前に補足。被除数「ax」、除数「ay」で、「ax > ay」です。
それ以外の場合(ax = ayやax < ay)は、文字列数処理のところで０か１にしています。
では説明です。

  • １～５行目は下準備。

    • N桁÷M桁⇒N-M+1桁になるので、_lz = _lx - _ly +1です。

  • _ys：_y に 1～9 を掛けて、VSTACK関数で縦に並べています。

    • 例えば、_y = 3 の場合、

    • _ys = { {3,0}, {6,0}, {9,0}, {2,1}, {5,1}, {8,1}, {1,2}, {4,2}, {7,2} }

    • 注）配列数は左右が逆になっています。普通に書くと{03,06,09,12,15,18,21,24,27}

    • 最初にこのリストを作っておくことで、毎回計算が走らないで済むようにしました。

  • _z：本丸です。最も苦労しました。正直詰みかけた・・・

    • 初期値：{ 答え(文字列数), 余り(配列数) }

    • ループ配列：_lz からの逆順

    • _sx：_xから比較する部分を切り出し

      • 計算途中で余りが０になることもあり、その時はエラーがでるので、０を返すようにしています。

    • _cmp：_sxと_ysを比較。結果は縦長のリストに保存。

      • _AnCmp関数は配列数の大小比較をする関数です。返り値は、

        • １：第１引数が第２引数より大きい

        • ０：等しい

        • －１：第１引数が第２引数より小さい

    • _m：_ysの何番目でオーバーしたかを調べ、その１つ手前の数を答えとして_mに代入。

    • _ym：_m番目の_ys。

    • _sym：_xと桁が合うように_ymをシフト

    • _dx：_x から _symを引き算。これが余り。

    • これを_lz回ループして、答えを増やしつつ、余りを減らします。

  • 出来上がった_zから、先頭列の答え(文字列数)を取り出し、配列数に戻して終了です。

最終的に文字列数で答えを出すので、わざわざ配列数に戻す必要もないかとも思ったのですが、配列数関数が文字列数を返してしまうと、他の関数との整合性がとれないのが気持ち悪かったので、こうしています。

さて、こんな複雑な処理をした筆算版割り算は動くのでしょうか？
検算結果です。

10桁÷5桁の割り算（筆算）

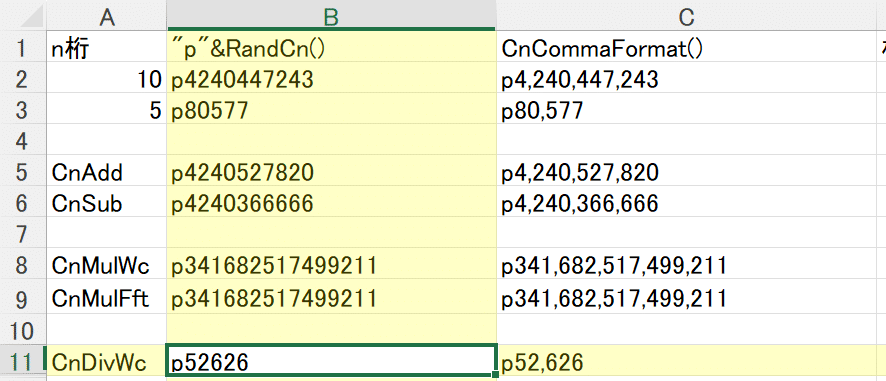
大丈夫なようです。
ちょっとデバッグ不足なので、まだまだ安心はできませんがひとまず完成しました。

ニュートン＝ラフソンの割り算アルゴリズム

一般にニュートン法と言われる手法のようですね。
「ラフソン(ラプソン？)」の方はジョゼフ・ラフソン(Joseph Raphson)というイギリスの数学者らしいですが、よくわかりません。
長いのでニュートン法と呼んでおきます。
このニュートン法での割り算に関しては、たくさんの説明が巷にありますので、ここではどのようにコードを書いたかだけ説明します。
まず、考え方。

  • 除数を$${B}$$、被除数を$${A}$$としたとき、除数の逆数$${1/B}$$を被除数に掛ければ、割り算の答えが求められる。

    • 例えば$${A=20,B=6}$$のとき、$${1/B=0.166}$$なので、$${A×1/B=20×0.166=3.32}$$

  • ここで、$${ y = 1/x - B}$$という方程式を定義し、$${y=0}$$のときの$${x}$$を求めれば、$${B}$$の逆数が得られます。

  • ここから、図とかが無いと説明が難しいので、すっとばして＾＾；、次の式で近似値を求めます。$${x_{n+1} = 2×x_n - B×x_n^2}$$

さて、何が何だか仕組みは分からないが、考え方はわかった！
でも逆数は不動点少数だけど、どうすればいいの？という疑問に答えてくれる記事を見つけることができませんでした・・・。
というわけで次の様に考えます！

  • $${x_n = X_n/D, D=10^d}$$、Ｘは整数で、dは精度ですね。dが10なら小数点以下第10位までの精度という考え方。

  • これを上の式に代入、$${X_{n+1}/D = 2×(X_n/D) - B×(X_n/D)^2}$$

  • 式変形すると$${X_{n+1} = (2DX_n - BX_n^2)/D}$$

  • これを繰り返して近似値のD倍の数値を求め、Aに掛けた後でDで割れば求まるはず！

と、いうわけでコードです。

Function Name : _AnDivNm

Discription : 配列数の除算。ニュートン法

Argments : ax, ay

Function definition :
=LET(
    _x, ax,
    _y, ay,
    _lx, COLUMNS(_x),
    _ly, COLUMNS(_y),
    _ac, _lx,
    _ad, HSTACK(SEQUENCE(, _ac, 0, 0), 1),
    _aa, DROP(_ad, , _ly),
    _ry, _Reciprocal(_aa, _ac, _y),
    _z1, _AnMulFft(_x, _ry),
    _z2, DROP(_z1, , _ac),
    _dx, _AnAdd(_x, -1 * _AnMulFft(_y, _z2)),
    IF(_AnCmp(_y, _dx) = 1, _z2, _AnAdd(_z2, 1))
)

逆数を求める部分を全て_Reciprocal関数に任せているため、こっちはシンプルですね。

  • _ac：精度。今はaxの桁数と同じにしています。

  • _ad：上の考え方のDにあたる部分です。分母ですね。

  • _aa：逆数の初期値です。

    • これをどのように設定するのが適当なのかが良くわかりません。っ詳しい人、教えてください。

  • _ry：_yの逆数ですね。関数内は後ほど。

  • _z1：_xに_ryを掛けます。掛け算はFFT版を使っています。

  • _z2：_z1をシフトダウンしてます。Dで割るのと同じ処理です。

  • _dx：誤差補正のため、_xから_y×_z2を減算して余りを出しています。

  • 最後に余り_dxが_yより大きければ、１を足して補正します。

では、肝心の_Reciprocal関数です。

Function Name : _Reciprocal

Discription : ニュートンアルゴリズムで逆数の近似値を求める。１００回上限。
aa:初期値,ac:精度,y:除数,i:回数			

Argments : aa, ac, y,[i]

Function definition :
=LET(
    _i, IF(ISOMITTED(i), 1, i),
    _b1, _AnAdd(aa, aa),
    _b2, HSTACK(SEQUENCE(, ac, 0, 0), _b1),
    _c1, _AnMulFft(aa, aa),
    _c2, _AnMulFft(y, _c1),
    _d1, _AnAdd(_b2, -1 * _c2),
    _d2, DROP(_d1, , ac),
    IF(OR(i > 100, _AnCmp(aa, _d2) = 0), _d2, _Reciprocal(_d2, ac, y, _i + 1))
)

再帰をつかっています。
では、説明します。

  • _i：再帰関数なので、バグで永久ループしないようにカウントを取っています。_iが100以上になったらストップです。

  • $${X_{n+1} = (2X_n×D - X_n^2×B)/D}$$

    • _b1：$${2X_n}$$にあたる部分です。掛け算ではなく足し算で処理。

    • _b2：$${2X_n×D}$$です。掛け算せずにシフトで高速化してます。

    • _c1：$${X_n^2}$$です。これは掛け算を使うしかないですね。

    • _c2：$${X_n^2×B}$$です。

    • _d1：$${2X_n×D - X_n^2×B}$$です。

    • _d2：$${D}$$での割り算です。これもシフトで対応しています。

  • 最後が終了判定です。_iが100を超える or aa = _d2の場合に終了しています。

では、結果を見てみましょう。

10桁÷5桁の割り算（ニュートン法）

問題ないようです。
こちらもデバッグが足りないので、どうなるかわかりませんがひとまず完成ということで。
では、計算速度を比べてみましょう。

1000桁÷10桁　速度比べ

あれ？ニュートン法が遅い・・・

1000桁÷500桁　速度比べ

除数が大きくなると速度が逆転するみたいですね。
もう少し大きな数も試してみます。

10000桁÷2000桁　速度比べ

ここまでいくと、反応が無くてハラハラします。
それにしても、ニュートン法はあまり早くなってなくて残念ですね。
桁数がもっと大きくなれば違うのでしょうが、これ以上は心臓に悪いので試したくないですね。

ゴールドシュミットの割り算アルゴリズム

さて、３つ目はゴールドシュミットの割り算アルゴリズムです。
が、これ、何度試してもうまくいきません。
ニュートン法とは別の手法で除数の逆数を求める方法なのですが、うまく収束しません。
なので、今回は諦めました。
また機会があったら試してみたいと思います。

勉強結果

こんかいの勉強結果です。

デバッグよろしくお願いします。

追記（2025/2/6）

少しだけニュートン法を改良できたので、さらしていきます。
コメント欄でも話題にしている「初期値」をいじりました。
とりあえず、コードを。

Function Name : _AnDivNm

Discription : 配列数の除算。ニュートン法

Argments : ax, ay

Function definition :
=LET(
    _x, ax,
    _y, ay,
    _lx, COLUMNS(_x),
    _ly, COLUMNS(_y),
    _aa, _AnDNInitialValue(_x, _y),
    _ry, _Reciprocal(_aa, _lx, _y),
    _z1, _AnMulFft(_x, _ry),
    _z2, DROP(_z1, , _lx),
    _dx, _AnAdd(_x, -1 * _AnMulFft(_y, _z2)),
    IF(_AnCmp(_y, _dx) = 1, _z2, _AnAdd(_z2, 1))
)

前回と違うのは、

_aa, _AnDNInitialValue(_x, _y),

ですね。
前回のコードは、

_ac, _lx,
_ad, HSTACK(SEQUENCE(, _ac, 0, 0), 1),
_aa, DROP(_ad, , _ly),

ですね。
例えば、被除数「_x」の桁数「_lx」が５、除数「_y」の桁数「_ly」が4だとすると、「_ad = 100,000」で、「_aa = 10」となります。
「_y」が1000でも9999でも同じです。
新バージョンではこの部分を関数に突っ込みました。
別に再帰を使っているわけでもないので、関数化する必要もないのですが、結構複雑でバグりまくって、何度もマシンがフリーズしたので、切り分けてデバッグしながら作りました。
コードがこちら。

Function Name : _AnDNInitialValue

Discription : ニュートン法でayの逆数を求める際の初期値を算出する

Argments : ax, ay

Function definition :
=LET(
    _x, ax,
    _y, ay,
    _lx, COLUMNS(_x),
    _ly, COLUMNS(_y),
    _in, 15,
    _ry1, SUBSTITUTE(1 / _AnToCn(TAKE(_y, , -1 * _in)), ".", ""),
    _fe, IFERROR(FIND("E-", _ry1), 0),
    _ry2, IF(_fe = 0, _ry1, REPT("0", VALUE(RIGHT(_ry1, 2))) & LEFT(_ry1, _fe - 1)),
    _ry3, VALUE(MID(_ry2, SEQUENCE(, LEN(_ry2)), 1)),
    _lry, _lx + 1,
    _ry4, IF(COLUMNS(_ry3) > _lry, TAKE(_ry3, , _lry), EXPAND(_ry3, , _lry, 0)),
    _ry5, SORTBY(_ry4, SEQUENCE(, COLUMNS(_ry4)), -1),
    _ry6, IF(_ly <= _in, _ry5, DROP(_ry5, , _ly - _in)),
    _AnCarryAndFix(_ry6)
)

先にやりたかったことを書くと、$${10^{lx}/y}$$を出したかっただけなんですが、Excelの数値の制約のせいで、こんな例外処理だらけになっています。
一応、説明をば。

  • _in：_y（被除数）の上位何桁を使用するか決めています。

    • 例えば、_y = 123なら、そのまま123。

    • _y = 123,456,789,123,456,789なら、123,456,789,123,456

  • _ry1：1/(_yの上位15桁)

    • 例えば、_y = 123なら、1/123 => 0.00810081 => 000810081

    • _y = 123,456,789,123,456なら、1/_y => 8.1E-15 => 810000006561005E-15

  • _fe：_ry1の中に”E-"があれば、その位置を取得

  • _ry2：”E-"を"0"に変換

    • 810000006561005E-15 => 00000000000000081000000006561005

  • _ry3：_r2を配列に変換

    • ※まだ「配列数」にはしていません。

    • 000810081なら、{0,0,0,8,1,0,0,8,1}

  • _ry4：配列数を_lx + 1にそろえる。

    • _lx = 5なら、{0,0,0,8,1,0,0,8,1} => {0,0,0,8,1,0}

    • _lx = 10なら、{0,0,0,8,1,0,0,8,1} => {0,0,0,8,1,0,0,8,1,0}

  • _ry5：_ry4を左右反転

  • _ry6：_ly >= _in の場合の桁調整

  • 最後に_AnCarryAndFixに突っ込んで、先頭の０を削除

このコードは果たしてあっているのだろうか？
かなり自信がありません・・・
しかし、計算結果はあっているので、おそらく正しいのでしょう！
では、速度調査です。

10000桁÷2000桁　速度比べ再び

確かに早くなっています！
しかし、こんなに苦労したのに劇的には変わっていない・・・残念。
割り算はトラウマになりそう・・・

ここまでの勉強結果を置いておきます。

デバッグ宜しくお願いします。

いいなと思ったら応援しよう！