
【騎士の旅路】ナイトがチェス盤を旅をするナイトツアー(騎士巡回問題)【数学パズル】
ナイトツアーについて
ナイトツアーとは、「チェス盤上でナイトの駒を動かし、すべてのマス目をたった一度だけ通過することができるのか」という問題になります。
ナイトはチェスの中でも特殊な動きをする駒で、「今いるマス目から上下左右に2マス、そこから垂直方向どちらかに1マス」移動することができます。
将棋でいう桂馬と同じ動きに似ていて、桂馬は前方方向に2マス進む動き方しかできないのに対し、ナイトは前後左右のすべての方向に動くことができます。
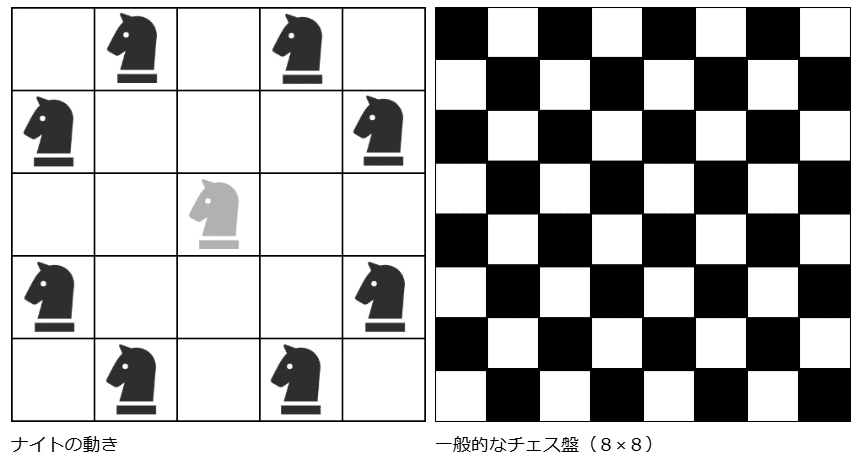
一般的なチェス盤は8マス×8マスになっています。
結論から言ってしまえば、8×8のマス目に関してはナイトツアーを完成されることができます。下の例はその一例になっていて、数字を順番にたどっていくことですべてのマス目をたった一度だけ通ることができます。

これ以外にもナイトツアーが完成するような順路は数多く存在しています。
自分の手で他のルートを探してみるのも楽しいと思いますよ!
一番最後にスタートした位置に戻ってこれる?
ひとまず、8×8のマス目に関してはナイトツアーを完成させることができることがわかりました。
では、8×8のチェス盤の上で、最後に出発地点に戻れるようにすべてのマス目をたった一度だけ通るような順路は存在するでしょうか。
実はこのような順路は存在しません。
考えると意外と簡単で、チェス盤の上を動くナイトは ⋯ →白→黒→白→黒→⋯ といったように、白と黒のマス目を交互に移動していきます。
そして、最後に出発地点に戻るとすると最初のマス目から64回移動して最初のマス目に戻ってくるということですから、出発地点が白とすると、64回移動した後のマス目は必ず黒になります。出発地点のマス目の色を変えることはできませんから、このような順路は存在しないということになります。
他のサイズのマス目ではどうなるか
ここまでは実際のチェス盤に則って8×8のマス目でのナイトツアーを考えてきました。
では、他のサイズのマス目ではどうなるでしょうか。
下の例は5×5のマス目でのナイトツアーになっています。
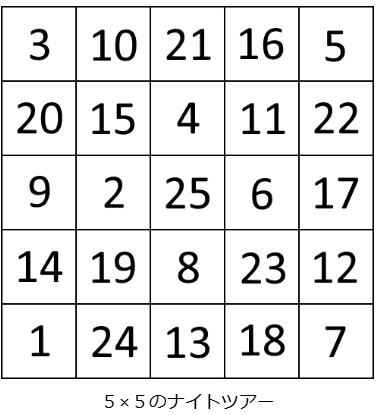
このように、5×5のマス目においてもナイトツアーを完成させることができました。
ここで直感的に分かる方もいらっしゃると思いますが、5×5以上のマス目についてはナイトツアーを完成させることができます。証明は長くなるので省略させてください。(いずれ書くかも)
では、さらに小さいマス目ではどうなるでしょう?
まずは、3×3のマス目についてですが、真ん中のマス目と行き来できるマス目が存在していないため、ナイトツアーの条件である、「すべてのマス目を通過する」ことを満たすことができません。
つまり、3×3のマス目についてはナイトツアーを完成させるような順路は存在しないということがわかりました。

2×2のマス目についても同様で、すべてのマス目についてナイトの動きでは移動することができないので、2×2のマス目についてもナイトツアーを完成させるような順路は存在しないことがわかります。
5×5のマス目では出来て、3×3のマス目では出来ない、じゃあ4×4はどうなの?ということになります。
結論を言ってしまうと、4×4のマス目でもナイトツアーを完成させる順路は存在しません。
証明は長くなってしまうので割愛させていただきます。
簡単に、私が考えた証明の概要だけ説明しておこうと思います。少し分かりづらいかもしれないので、読みとばしていただいても構いません。
証明の概要
ナイトツアーが成立する条件である「すべてのマス目をたった一度だけ通る」ということから、

上の画像のように、角のマス目に移動することができるマス目は必ず2つだけであり、これが4か所の角で成立しているということになります。角を出発地点・終着地点にすることで2か所については無視することができますが、それ以外の2か所については角に移動できるマス目に移動してきたときには必ず角に移動し、そこから角に移動できるマス目で先ほどいなかった方のマス目に移動しなければならない、ということになってしまいます。
つまり、動き方が固定される部分がある、ということです。また、マス目が対称であることを使って総当たり的に、この動き方ではダメ、この動き方でもダメ、これでもダメ、とナイトツアーが成立しないような動き方を探していき、結局すべてのルートがダメでした。という流れで証明を行いました。
まとめ
これまでの結果をまとめると、
自然数$${N\geq5}$$に対して、$${N\times N}$$のマス目はすべてのマス目をたった一度だけ通るような順路が存在し、自然数$${N\leq 4}$$に対しては存在しない。
ということになります。
今回紹介したナイトツアーは縦と横のマス目の数が同じような場合でしたが、縦横が異なるマス目についても同様に考えることができますし、3次元以上の次元に拡張して考えることもできたりします。
高次元verについてはこちらを御覧ください。
