
電気のおはなしその60・コンデンサーに交流電圧を掛けたときの電圧・電流・電力(&並列共振)
前回がコイルでしたので、今回はコンデンサーです。
…コンデンサーはコイルの挙動を180°逆にしただけなんですけどね。
って、それで終わりにするのも寂しいので、ちゃんと書いてみますよ。
電気のおはなしその47・コンデンサー(2)電流が先、電圧があとでも書いたように、コンデンサーって奴は
電圧が掛かった瞬間、極板間電圧はゼロで、全力で電流を流し込む。しかし、流れ込んだ電流が極板にたまった結果、後から極板間電圧が上昇する。
という人だったんですね。まるで、食べ放題ビュッフェだからって空腹だからと目一杯食べだして、後からお腹一杯になって苦しんでる人みたいな
こういう性質のコンデンサーに交流電圧を掛けたらどうなるのでしょうか。これも挙動はすでに知られていて、電圧に対して電流が90°進んで流れる、ということが分かっています。実際の波形の例は、次の通りです。

コンデンサーの場合も、瞬時値を使って電圧÷電流を求めることはできないため、
オーム値=電圧の実効値÷電流の実効値
で計算します。そして、コイルと同様に、この値のことを「リアクタンス」と呼びます。コンデンサーの性質の大きさである静電容量と、ある周波数fに対するリアクタンスの関係は、

で求められます。単位はΩです。
コイルとコンデンサーでは位相の進み遅れが逆になるため、それらを区別する必要がある場合は、
コイル:誘導性リアクタンス
コンデンサー:容量性リアクタンス
と呼び分けています。
コンデンサーに交流電圧を掛けたときの電力についても、グラフから求めることができます。
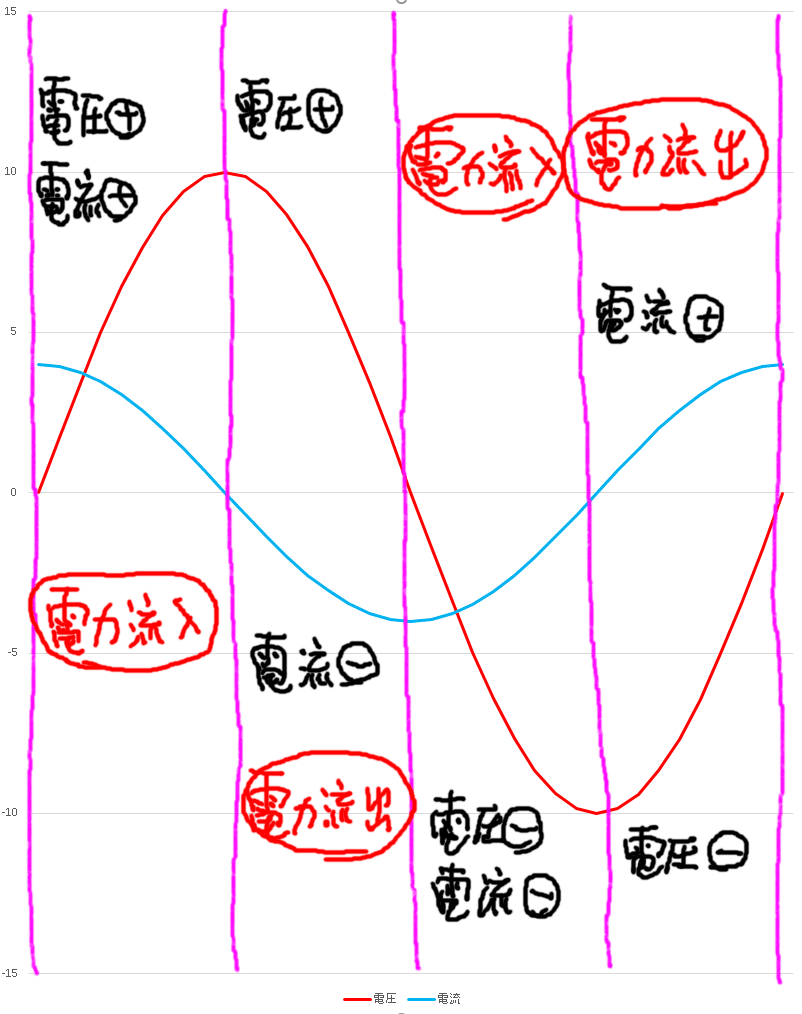
このように、コイルの場合と同様、
電力流入 → 電力流出 → 電力流入 → 電力流出 → 電力流入
を1/4周期ずつ繰り返しているということが分かります。そして、
コンデンサーは、1/4周期で流入する電力を静電エネルギーとして蓄え、次の1/4周期で静電エネルギーから電力を作り出して放出し、次の1/4周期でまた流入する電力を蓄え、そして放出…を繰り返しているので、コンデンサー自身は電力を消費しない
ということになります。
はい、それではめでたしめでたし…
ではなく
コイルとコンデンサーを組み合わせたことを考えてみますよ。

左がコイル、右がコンデンサーですが、電圧の波形は同じ形であるのに対し、電流の波形は互いに180°反転した形となっています。
では、コイルとコンデンサーを並列に接続したらどうなるでしょう?

この回路に交流電圧を掛けると、コイル・コンデンサーに電流が流れます。

すると、コイルから流出した電流は、同じタイミングで電流を流し込むコンデンサーに流れ込みます。コンデンサーが電流を流出させているタイミングでは、コイルがその電流を流し込みます。したがって、
コイルとコンデンサーの間で相互に電流がやり取りされる
ということになります。そして、交流電源から流れ込む電流は
電源電流=|(コイルの電流)ー(コンデンサーの電流)|
つまり、コイル電流とコンデンサー電流の差が流れ込むことになります。
それでは、もしコイルのリアクタンスとコンデンサーのリアクタンスが同じ値だったらどうなるでしょうか?
この場合は、
コイルやコンデンサーには電流が流れているにもかかわらず、電源から流れ込む電流はゼロ
となります。この状態を並列共振と呼び、
コイルとコンデンサーで無効電力を打ち消しあうことで、リアクタンスを打ち消してゼロにすることができる
という特徴的な性質を持ちます。この性質を利用し、電力の世界では力率改善を図ったり、電気通信の世界では信号や電波を発振したりしています。つまり、コイルやコンデンサーの性質が無かったら、今の世の中の情報通信が根底から成立していなかったということになるわけですね。
ちなみに、同じリアクタンス値のコイルとコンデンサーを直列に接続した場合は、直列共振という状態になります。直列共振の挙動がどうなるかは、ちょっと考えてみてくださいね。
以上。
