
電気のおはなしその22・線形回路とその性質(2)
今回は、本当は「重ね合わせの原理」に行こうかと思っていたのですが、手抜きをするためもう一問出題したいと思ったので、前回の続きということにしましたよ。
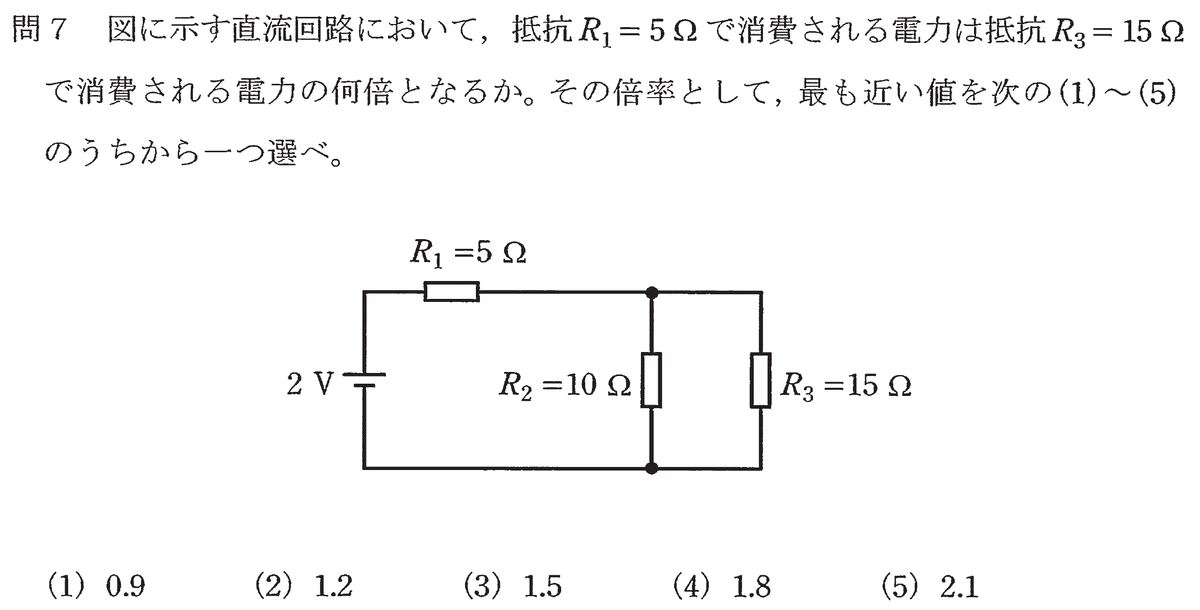
この回路も、電池と抵抗だけの回路ですから線形性が成り立ちますし、「抵抗R1で消費される電力は抵抗R3の何倍か」という形式の問題ですから電源電圧に関係なく比率が求まるんじゃないか?という感じがします。
でも、電圧と電流はいいとして、電力も同じ法則が成り立つのでしょうか。
…おおっと、これまでに「オームの法則」は説明しましたが、「抵抗で消費される電力」の話をしていませんでしたね。
これをご覧のかたがたは、ほとんどご存じかと思いますが、抵抗で消費される電力は
(抵抗の両端の電圧)×(抵抗に流れる電流)
P=V×I
で求めることができます。なお、オームの法則を適用することにより、
P=V×I=(R×I×I)=(V×V÷R)
と変形することもできます。
これを、物理学的な「仕事」の立場から考えると、仕事=力×距離でしたから、力が電圧、距離(電流の正体である、電子の移動距離)は電流に対応しますので、イメージができるかと思います。
なお、電流は「1秒間に1クーロンの電荷量が流れるのが1アンペア」ですから、電力というのは1秒間の間に発生する仕事量となります。
抵抗器は、このようにして消費される電力を熱として放出する素子で、発生する総熱量は、
(熱量)=(電力)×(時間)
となります。これは、500Wの電子レンジで3分加熱するのと1000Wの電子レンジで1分半加熱するのと1500Wの電子レンジで1分加熱のがおおよそ同じ程度の温まり方になることからも分かるかと思います。
さて。では元の回路に戻りましょう。

出題は、R1とR3の消費電力を比べる問題でした。
ここで、線形回路の性質にさかのぼって考えてみます。
R1・R2・R3のいずれも、電源電圧を2倍にすれば抵抗に掛かる電圧も抵抗に流れる電流も2倍になります。5倍にすればどれも5倍です。
ここで、電源電圧が2Vの場合のR1の消費電力をP1、R3の消費電力をP3とします。さて、電源電圧をN倍にしたら、それらはどうなるでしょうか。
まず、R1に掛かる電圧がN倍、R1に流れる電流もN倍になりますから、R1で消費される電力はN^2倍になります。つまり、N^2・P1です。
同様にしてR3について考えると、やはり電圧がN倍、電流もN倍ですから、消費電力はN^2・P3となります。
以上のことから、
消費電力の比も、電源電圧に関係ない
ことが分かります。したがって、電源電圧を2Vではなく、計算しやすいような値に勝手に変えてしまっても答えは変わらないことになります。
では具体的に何ボルト・何アンペアに設定すれば良いか?は好き好きで良いのですが、ここではR2とR3の並列部分に掛かる電圧が30Vということにします。理由は、電流の値が割り切れるから。
というわけで、以下が段取りです。

R2・R3の両端の電圧を30Vとおく。
R3に流れる電流を求める。2Aと求まる。
R3の電力を求める。30V×2A=60Wとなる。
R1に流れる電流を求める。R2に3A流れるので、5Aと求まる。
R1の電力を求める。P=VI=I^2Rで125Wと求まる。
で、正解は125÷60≒2.08≒2.1倍と求めることができます。
今回の問題も、確かに電源電圧が2Vのときの各部の電圧や電流を求め、実際の消費電力を求めることで答えを導くことも可能ではあります。
しかし、こうして見ると「回路の線形性」に気付くかどうか、というのは非常に大きなアドバンテージになる、ということがお分かり頂けたのではないかと思います。
「線形性」自体は、前回もお話ししたように、「オームの法則により、Rが一定であれば電圧も電流も比例関係にある」という当たり前のことしか使っていません。
ね?意外と行けそうな気がしてきたでしょ?
ということで暗示をかけて今回は終わりとします。
以上。
