電気のおはなしその45・コイル(4)コイルの過渡現象に関する重要問題演習
今回からコンデンサーの話に行こうかと思っていましたが、コイルの基本的な性質について完全に理解して欲しいと思いましたので、ちょうど良さそうな練習問題を取り上げてみることにしますね。これでコイルの過渡現象の定性的な理解はバッチリ!?(回路電流などの数学的な理論については、また別のタイミングでお話ししようと思っています)
まずは、電験3種の2009年、理論問10から行きます。
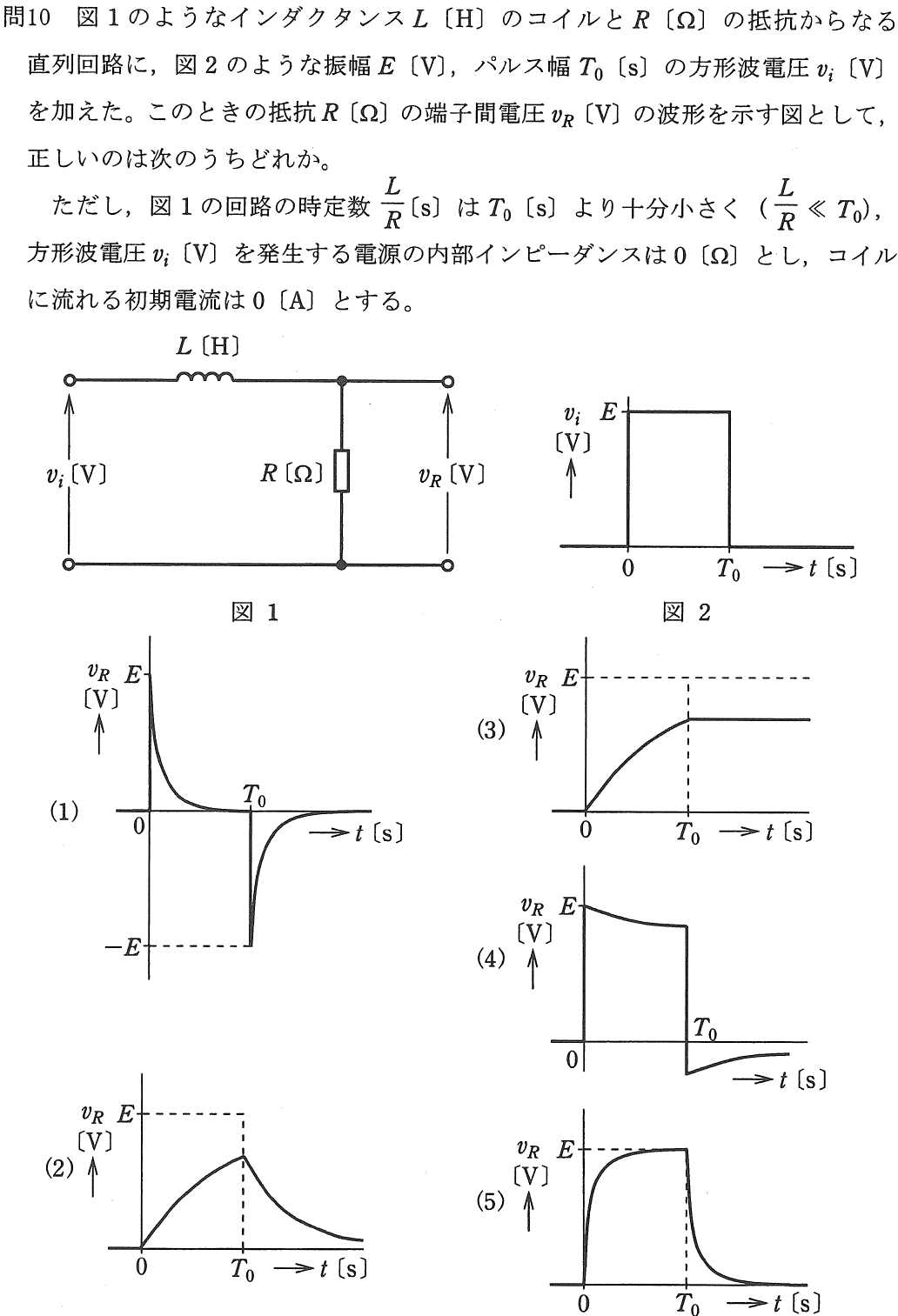
「時定数」というのは、過渡現象が落ち着くまでの時間の目安の値です。抵抗とコイルが接続された回路は、スイッチを入れた瞬間からしばらくの間は時間経過に伴って電圧や電流が変化するわけですが、それが落ち着き、概ね電圧や電流の変化が落ち着くまでの時間という意味合いです。
その時間を計算する計算式は、自然対数の底とか微分・積分が絡んでくる難しい式になりますが、概念的には
コイルの大きさ(インダクタンス)が強いほど、コイルが電流変化に対して強く抵抗するため、時間変化の収束までに時間がかかる
でも、抵抗Rの値が大きいと、そもそも回路に流れる電流が小さいところで電流変化が終わってしまうので、抵抗Rの値は小さいほうがより収束には時間がかかる
ことが予想できるかと思います。
この直感の通り、この回路の時定数は
τ=L/R
で求めることができます。(時定数そのものの計算って超簡単なんです)
さて、スイッチを入れた瞬間、t=0のときの回路図は次の通りになります。
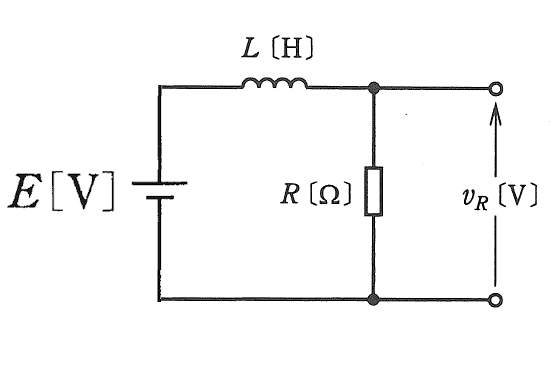
前回、
コイルの性質として、「両端に電圧が掛けられた瞬間、コイルは内部に電流を流したくないので、全力で抵抗する」ということを話しました。つまり、スイッチを入れた瞬間にコイルに流れる電流はゼロなのです。
と書いたとおり、スイッチONの瞬間に流れる回路電流はゼロですから、その時のvRはゼロなはずです。したがって、少なくとも選択肢(1)(4)は誤りです。
このあと、コイルには電流が流れるようになり、最終的にはゼロΩの単なる電線と同じになるのですが、出題文に「時定数はT0より十分小さい」とありますので、これは「時刻T0の段階で、もう電流変化は既に終わっている」ことを意味します。つまり、T0のときの回路は、等価的に次のようになっています。
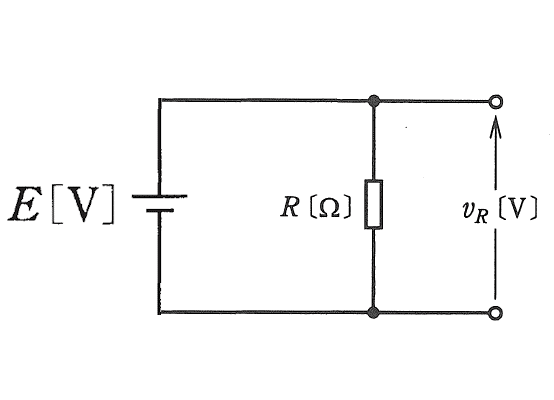
したがって、時刻T0の段階で出力電圧はEのはずですから、この時点で該当する選択肢は(5)しかありません。
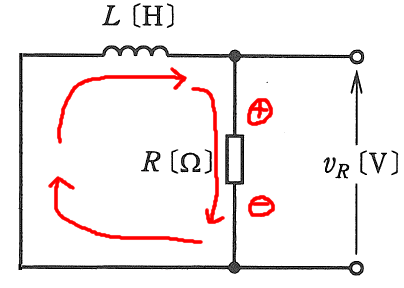
念のため、時刻T0の直後の回路図を考えると次のようになります。コイルの性質として、「流れている電流を切ろうとすると、今流れている電流を維持するような電圧を発生」しますから、T0直後のvRは、上側が+、つまりグラフ上では正の電圧となり、それがだんだんと減少していって最終的にはゼロとなる、ということで解答(5)の通りのグラフで正しいことが分かりますね。
次は、電験3種の2012年理論問9です。

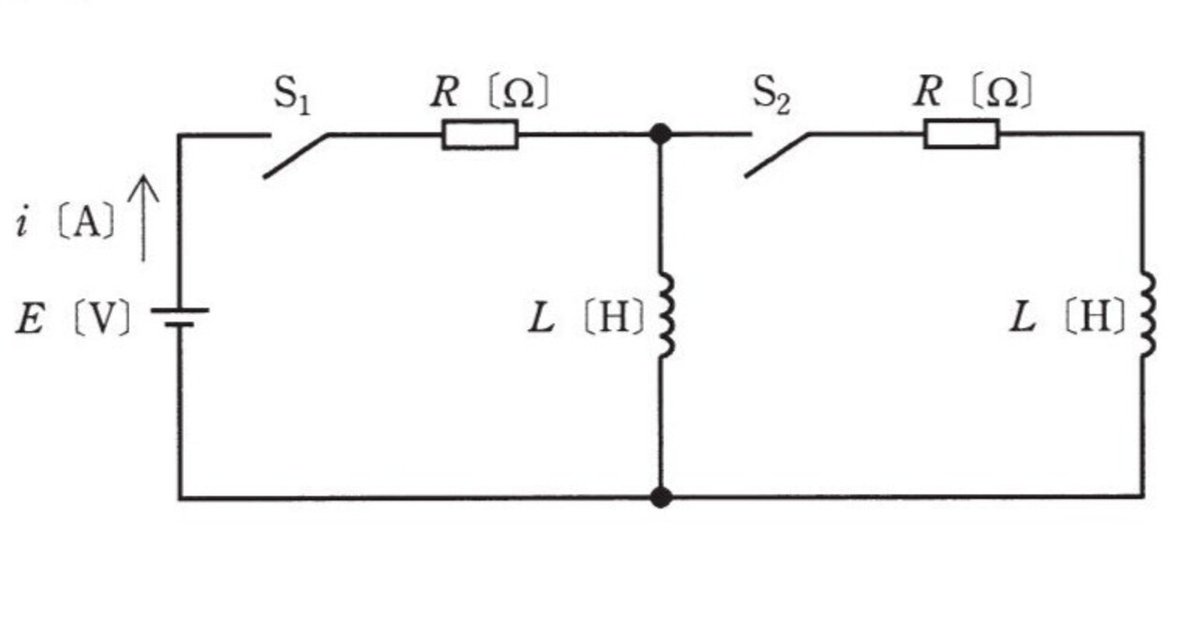
こんどは、コイルが2つでスイッチも2つあり、前問に比べると格段に難しくなったような印象があります。解答の選択肢は次の5択です。





では、例によって順番に見ていきましょう。
まず、t=t1の直後の回路は次のようになります。
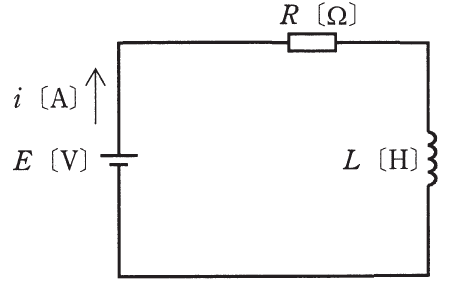
これも「スイッチを入れた瞬間にコイルは電流を流したくないので電流はゼロ」ですから、選択肢(1)~(5)のいずれもが正しい波形を描いています。
次に、十分時間が経過したとき、「コイルは単なる電線と同じに見なせる」ため、t=t2の直前の状態は次のような回路と見なせます。
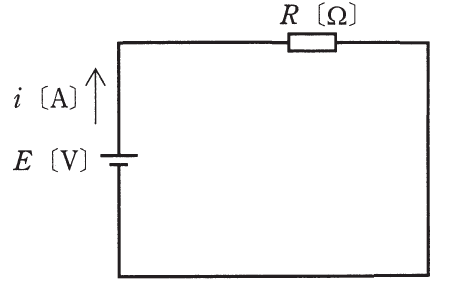
したがって、このときの回路電流はE/Rです。これも、回答選択肢(1)~(5)の全てが満たしています。
問題は、t=t2の直後です。このとき、既に左側のコイルは単なる電線と同じに見なすことができ、その両端の電圧はゼロです。したがって、S2を閉じた直後は、

このような回路になったと考えることができます。当然、回路に流れる電流はE/Rのままですから、正解は選択肢(3)です。
「え?そうは言っても、コイルと抵抗を並列にしたんだから電流とかは変わるんじゃない?」と直感的には思えるかもしれませんが、あくまでも「十分に時間が経ったとき、左側のコイルの両端の電圧はゼロ。電圧がゼロのところに並列に何をつなごうとも、回路の挙動は一切変化しない」わけですから、これで正しいことが分かるかと思います。
もう2000字近く書いてしまいましたが、最後にもう一問置いておきます。電験3種の2017年理論問10です。

「定常状態」というのは、過渡現象が終わって十分時間が経過し、回路に流れる電流などの変化が終わったということを意味します。
これまで説明してきましたコイルの挙動を理解していれば、ノーヒントで解ける問題かと思いますので、試しに考えてみてください。ちなみに正解は、
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
(1)でした。
以上。
