
電気のおはなしその11・クーロンの法則と電場(電界)の定義
さて、いよいよ電磁気学みたいな話に入りますよ。
電磁気学の教科書は、おそらくクーロンの法則

あたりから話がスタートするんじゃないかと思います。目にしたり暗記したりした方も多いことでしょう。
では、この式が表していることを改めて解説してみます。この式は、
Q1クーロンとQ2クーロンの電荷が距離r離れて存在するとき、電荷どうしに働く力Fを求める式
です。Q1とQ2の単位はクーロン、rの単位はメートル、Fの単位はニュートンで、4πεは、それらの間の辻褄を合わせるための係数です。
係数なら、別に4πεじゃなくてεだけで良いんじゃないの?と思いますし、実際高校物理の入門では「k」なんて係数で表したりしますが、この先もっと難しい理論を掘り下げていったとき、4πが付いているとうまく式が簡単になるので最初からこうしている、という風に思っておいてください。
さて、この式を、「電荷Q1が作る電場の中にQ2を置いたとき、電荷の間に働く力」という形に書き換えると、

となります。これは、Q1の電荷が、そこから距離r離れた場所に作る影響力の大きさが

であり、その点にQ2を置いたとき、

の大きさの力を受ける、という意味を持ちます。
もうお分かりの通り、

は、Q1クーロンが距離rの場所に作る電場(=電界)を表す式ということになります。
このように、点電荷が存在すると、その点を中心として距離rの2乗に反比例した電界が発生することが分かりますが、電界の強さは距離rによって決定されるため、点電荷が作る電界の強さが同じ点をつないだものは、点電荷を中心として同心円状に分布することがわかります。
「点電荷が作る電界の強さが同じ点をつないだもの」は「等電位面」を表すのですが、詳しくは電位の定義の話をした後にします。

こうやって図にすると、中心に高気圧があって、そこから周囲に向かって風が吹き出している様子とよく似ていますね。(実際同じようなもんです)
そして、中心に高気圧があるとき、その中に人間がいれば、風が吹いている方向に吹き飛ばされるのと同じで、このような電界の中に他の電荷を置くと、その電荷は中心から点電荷から離れる方向に力を受けます。(もちろん、中心の電荷と他の電荷の電気が+とー、もしくはーと+であれば、真逆の引きつけあう力となります)
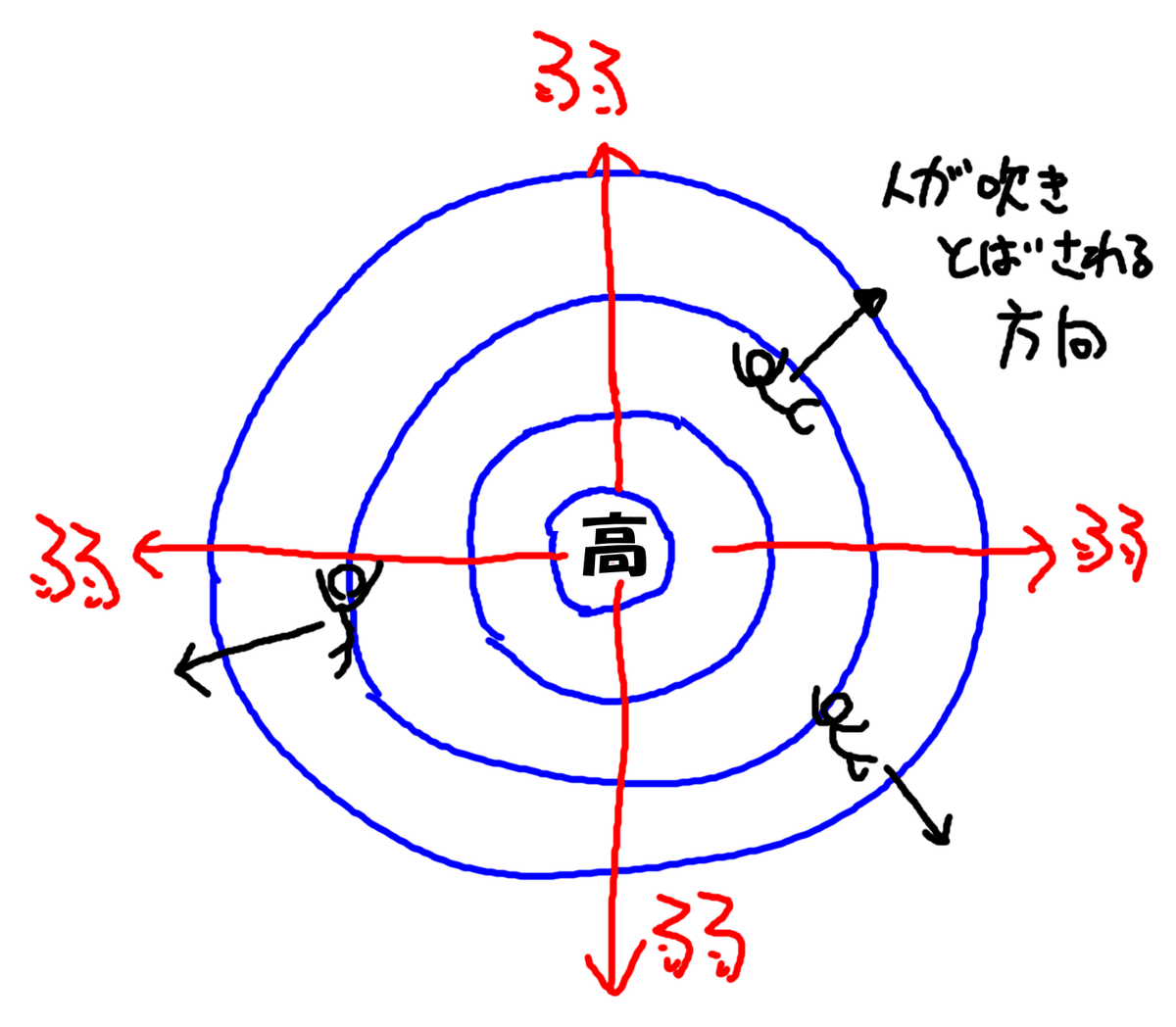

このように、ある電荷の周囲に他の電荷を置いたとき、他の電荷はどの方向に力を受けるのか、というのを表した線を電気力線と呼んでいます。その名のとおり、「電気」によって受ける「力」がどのようになっているかを表した「線」のことです。この図からも分かるように、電気力線と等電位面は常に直角に交わっていることが分かりますね。
電流の流れというのは、このような電界の中で電子が相互に力を及ぼしあい、そしてその力によって電子が移動していく現象ですから、電界を定義した次の段階としては、電界の中で電子が移動する場合の仕事(力×距離)を考えていくことになります。
この辺りまで来ると、次はベクトルを理解する必要がありますので、ベクトルの話に行きましょうかね。また、電位を考えるためには積分が必要となりますが、その辺もわかりやすく説明できればと思ってます。
電気理論から力学、電磁気学、そして数学に話が広がってきました。数学は数学で書き始めるとキリがないですし、力学と同様、数学は数学だけでひとまとめにしたスレッドにしたいところですけどね。
以上。
