
電気のおはなしその47・コンデンサー(2)電流が先、電圧があと
コイルの性質のとき、
磁界はとっても保守的で、磁界が発生していない状態から磁界を増やそうとすると、電磁石は磁界が増えない方向に抵抗します。逆に、既に磁界が発生している場所の磁界を取り去ろうとすると、今度は磁界が減らない方向に抵抗を試みます。磁界はメチャクチャ保守派なんです。
という話を書きました。要するに、
電流が流れると磁界が発生する。
磁界は変化を嫌う。
だからコイルに電圧を掛けてもすぐには電流が流れない。
つまり時間的に電圧が先、電流が後
だったわけです。電気の勉強をしていて多くの人がつまづき出すのが、このような「電圧と電流の間に時間差が発生する場合がある」点なのですね。
さて、それではコンデンサーの働きですが、これはコイルとは真逆の性質で、電流が流れ込むのが先、電圧が上がるのが後になるんです。
これは、コンデンサーを水槽に例えても分かります。



はい、明確に電流が流れ込むのがタイミング的に先、そしてその結果として電圧が上昇する(こちらが後)という因果であることが分かります。決して逆にはなりません。
これを回路素子としての挙動で考えると、コンデンサーは、その両端に直流電圧を掛けた瞬間、全力で内部に電流を流し込む性質として現れます。つまり、コンデンサーに電圧を掛けた瞬間の抵抗値はゼロと考えることができます。そして、電流が流れ込んだ結果として極板間の電圧が上昇し、電源電圧と同じ電圧になったら電流の流入が止まる、という挙動を示します。
これを、コイルの場合と同様、回路図と電流のグラフで表してみます。
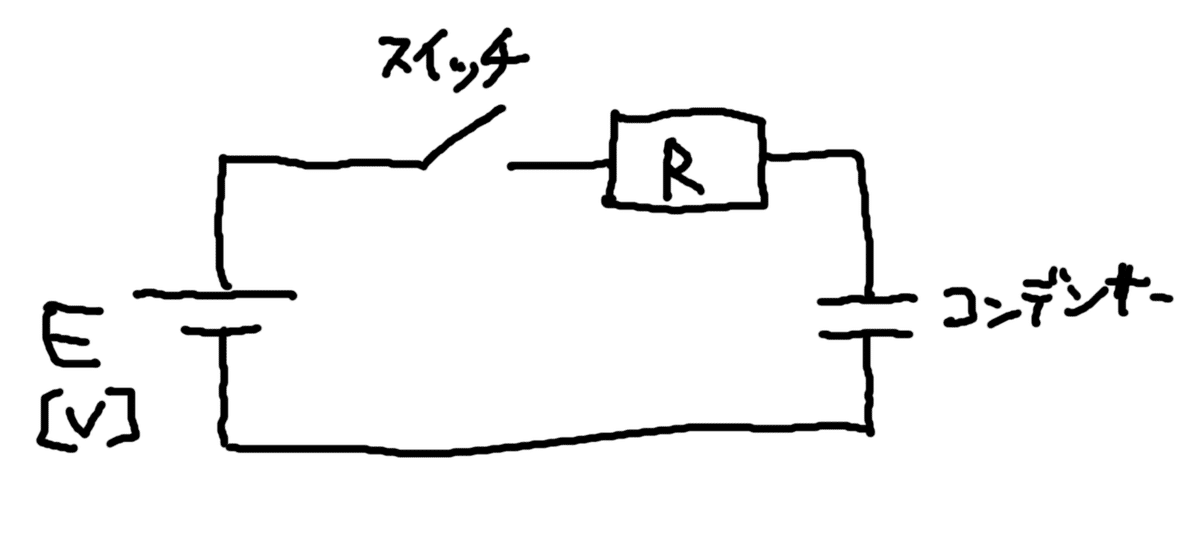
このような回路を作り、スイッチをONにした瞬間から回路に流れる電流の大きさをグラフ化すると、次のようなグラフになります。

このように、コンデンサーの場合は、コイルの場合のグラフを上下ひっくり返した形になります。

では何故、コイルとコンデンサーではちょうど真逆の性質になっているのか?これは、宇宙の原理がそうなっているからとしか言いようがない不思議な話です。理論的には、

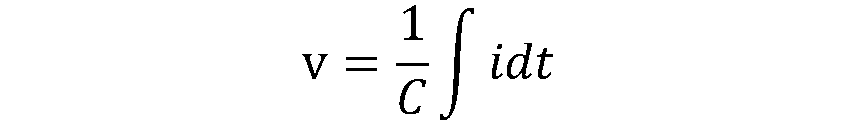
という形で表せるからだよー、ってことにはなるのですが、これとて自然現象が先に存在し、それを人間が数学という道具で表現したにすぎません。
そうそう、式を出したついでに、コンデンサーの静電容量の大きさと極板の大きさ(面積)S、極板間距離d、そして極板の間に挿入されている物質の誘電率εの間の関係は、

で表されます。極板の面積が広く、極板間距離が狭く、そして極板間に入れた物体の誘電率(前回、吸水性の高いスポンジなんて比喩を使いました)が大きいほど大量の電気を貯めこむことができることが分かります。
次回は、コイルの場合と同様に、実際に国家試験に出題された問題を使って回路素子としての挙動を見ていこうと思っていますよ。
以上。
