電気のおはなしその20・電験3種の抵抗の直並列問題を解いてみる(2)
前回に引き続いて、電験3種の理論の問題から1問ピックアップしてみます。

前回の問題(電験3種・平成25年・理論・問8)の考え方が理解できれば、解くのは簡単ではないでしょうか。

はい。上の5Ωは、外周をぐるっと回って両端が接続されているため、抵抗の両端の電圧はゼロです。したがって、この5Ωには電流が流れません。
そこで、この抵抗を取り外してしまいます。

すると、2本の10Ωは、外周をぐるっと回った経路を通じて、並列接続されていることが分かります。
…う~ん?と思った人は、次の図で。

こうすれば、10Ωの抵抗は、青いラインと赤いラインによって互いに接続され、確かに並列接続されていることが分かります。
したがって、この回路は、
25Vの電池に対して、20Ωと5Ωが直列になっているとき、回路に流れる電流はいくらか。
という問題になりますから、答えは1Aということになります。
もう一問いってみましょう。
第一級陸上特殊無線技士の、2021年2月期無線工学Aの問3です。

はい、このような回路の合成抵抗を求める問題です。

初見では「なんじゃこりゃー!?どう考えればいいんだ…」となるかもしれません。私も最初そうでした。
ここで使う考え方は、
回路中、電圧が同じ点どうしを接続しても電流は流れないので、回路全体の挙動は一切変わらない。したがって、電圧が同じ点同士を接続している線を撤去してしまっても、あるいは電圧が同じ点どうしを勝手に接続してしまっても、回路全体の挙動は変わらない
というものです。
この回路の対称性を考えて、a~b点のうち同じ電圧である点を接続した回路は、次のようになります。
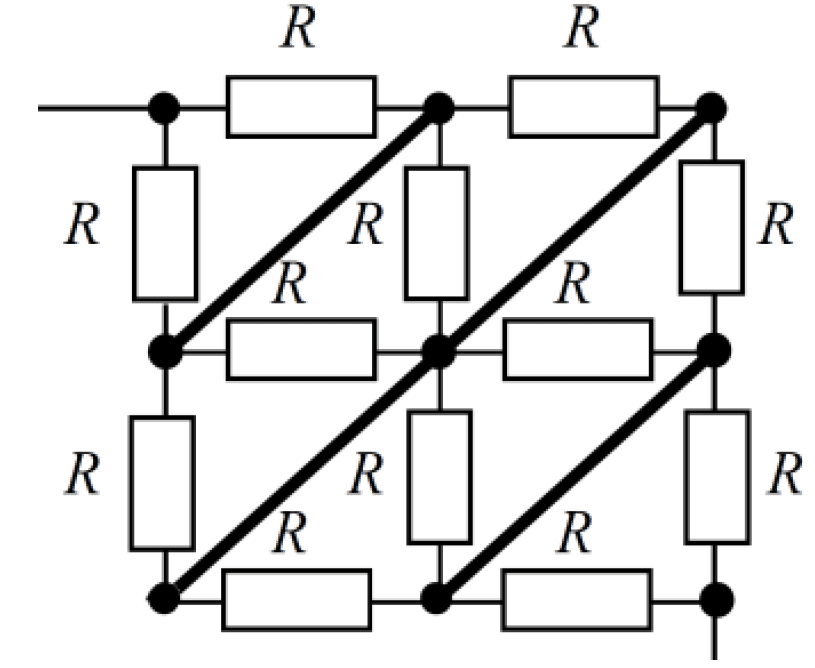
はい、ここまでくると、答えが見えてきたかと思います。
この回路は、
a点~Rの2本並列~Rの4本並列~Rの4本並列~Rの2本並列~b点
と接合された回路になるんですね。ビックリですね。
出題文より、抵抗が50Ωですから、25+12.5+12.5+25=75ということで、答えは75Ωということになります。
今回紹介したように、
電流の流れない抵抗などは取り外してしまうことができるし、電流の流れない電線は取り去ってしまうことができる
逆に、電圧が明らかに同じ点どうしを電線で結んでも回路全体の挙動が変わらないので、分かりやすくするためにあえて接続してしまう
というテクニックは、意外と有用です。
この後、どこかの段階で三相交流のお話をすることもあるかと思いますが、三相交流はこの理屈のうち、「電流の流れない電線は取り去ってしまうことができる」というのを利用して電線を減らしたものなんですね。
今回はこの辺にしましょう。
以上。
