電気のおはなしその55・交流の性質（７）円を省略するためのベクトル

前回、

交流の波形を考えるときは、そのタイミングを考えないと正しい答えが出ませんよー

というお話をしました。100Vの交流電源VaとVbを直列にしたらどうなるでしょう？という例題も、「位相差が分からないと求められません」というのが正解でした。

そこで、VaとVbの波形を円周上の点を用いて表現してみました。

図1・VaとVbを円で表した図

この波形二つを直列合成すると、その結果は

図2・VaとVb、Va＋Vbの時間波形

こんな形の波形になりました。

さて。

交流波形を表現する場合、このようにいつも円を描いていれば位相が分かりやすいのですが、円を描くのはスペースが必要なので、何とか円を省略することができないか？という話になります。

円を省略する…。

どうすれば、円を描かなくとも、「この波形は、円周上のこの点から回転するんだよ」ということを伝えられるでしょうか。

はい。

答えは、

円の中心と、円周上にある点を矢印で結んで見せる

ということになります。この二つがあれば、

図3・ベクトルから円を復元

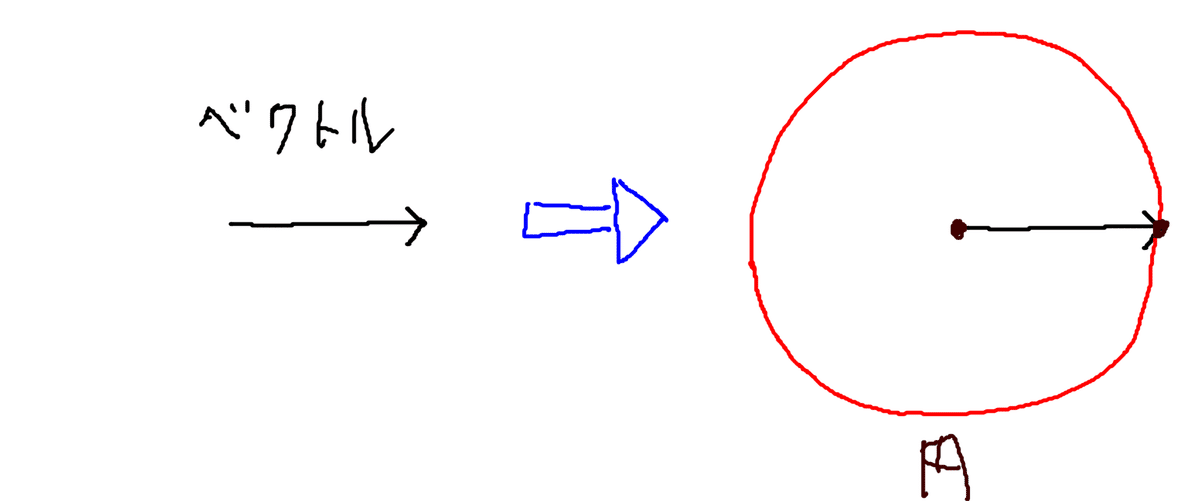
このように、円を復元して描くことができるようになります。

電気のおはなしその１２・スカラーとベクトル、ベクトルの和と差の計算の回で、「ベクトルって何？」ということを書きましたけど、今回のように「円の中心と円周上の点を結ぶ矢印」も立派なベクトルです。

…はい、そうなんです。
交流のベクトルというのは、

ある交流波形が、あるタイミングにおいて、円周上の一体どの点にあるのかを表現するために描く円を表現するため、円の中心点と円周上の点の間を矢印で結ぶことで表したもの

だったわけです。この基本を理解しないまま、「コンデンサーは上向き」「コイルは下向き」とやるから意味が分からなくなるわけですね。

それじゃ、いくつか例題を出して練習してみましょう。
まずは簡単な例から。

図4・位相差のないVaとVbの時間波形

このVaとVbをそれぞれベクトルで表してください。

…これはすぐ分かりますね。

図5・VaとVbのベクトル図

こうなります。
なお、別にベクトルを2本に分ける必要はなく、ひとつの図の上に重ねて表現することができますから、

図6・VaとVbを合成して描いたベクトル図

このように重なったベクトルで表現してもかまいません。

ところで、

図7・ベクトル表現するタイミング

この図のように、①や②、③のタイミングを使ってベクトルを描く、すなわち

図8・いろいろなタイミングで取ったベクトルの図

こんなベクトルを描いちゃいけないの？という疑問があるかもしれませんが、実はこれらのベクトルはどれも正解です。これでもOKです。
ただし、何か基準がないと分かりにくくなってしまうので、電源電圧とか負荷の電圧とか、あるいは電源の電流など、何か基準になるベクトルを基準（右向き）として表現する、というのが暗黙の了解になっています。

では、次の波形をベクトルにするとどうでしょう？

図9・180°の位相差を持つVaとVbの時間波形

もう分かりますね。正解は、

図10・図9をベクトルで表したもの

このようになります。ひとつの図にすると、

図11・図10をまとめて描いたもの

こんな感じですね。（手描きなので斜めになってますが、Vaが真右、Vbが真左です…）

では、次の場合は

図12・90°の位相差を持つVaとVbの時間波形

ベクトルだとこうなります。

図13・図12の波形のベクトル図

以上で、交流波形のベクトル図が一体何を表現しているのか、ということがお分かりいただけたかと思います。次回は、これらの電圧などを直列にした場合、合成電圧などをどうやって求めるのか？という核心部分についてお話しますね。

以上。