
電気のおはなしその23・重ね合わせの原理
電磁気学の話として、磁気回路の話やアンペールの法則、ファラデーの電磁誘導の法則、ガウスの発散定理など、色々と展開していきたい話はあるにはあるんですが、それらの話の前提として空間ベクトルの微分だの発散だの回転だのという話をしなければいけなくなるため、「話の簡単さ」の筋を取り、今回は重ね合わせの原理の方に進んでいくことにしましたよ。
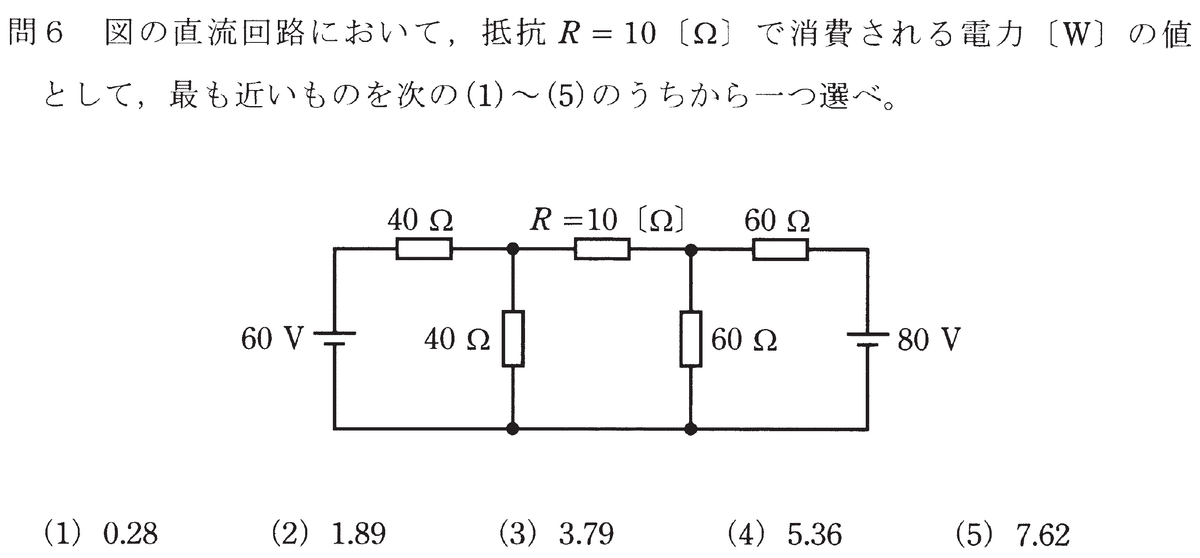
これも、試験の例題から話に入っていった方が分かりやすいかと思うので、電験3種の2013年理論問6を取り上げることにします。
あるいは、第一級陸上特殊無線技士の2017年2月期工学Aの問3も挙げてみますか。

このような、抵抗の組み合わせ回路において電源が複数含まれている回路の電圧や電流などを求める問題は、ちょっと一段ハードルが高くなるのではないでしょうか。もし電源が1個なら、抵抗の直列や並列の値を計算していき、時間が掛かろうとも何とか答えを出すことができても、複数の電源があると、さてどうしたらいいのか?と思われる方もいるかと思います。
このような場合、前回話したような「回路の線形性」が役に立ちます。俗に「重ね合わせの原理」とか「重ねの理」なんて呼ばれている原理ですが、
電源が複数存在する線形回路において各部の電圧・電流などを求める場合、どれか一つの電源のみを残し、他の電圧源は短絡、電流源は開放として各部の値を求め、それらを電源の数だけ行って求めた値の重ね合わせとなる
という理論です。
例えば一つ目の回路の場合、60Vの電源だけを残して80Vの電源は短絡し、各部の電圧・電流などを求めた値と、80Vの電源だけを残して60Vの電源は短絡し、同様に各部の電圧・電流などを求めた値を重ね合わせることで、両方の電源を生かした時の各部の電圧や電流を求めることができます。
二つ目の回路も同様で、左側の21Vの電源を残して右側の21Vの電源は短絡して4Ωの抵抗に流れる電流を求め、次に右側の21Vの電源を残して左側の21Vの電源を短絡し、4Ωの抵抗に流れる電流を求め、それらの値を足すことで電源を両方生かした場合の電流値を求めることができるわけです。
では実際に求めてみます。まず最初の問題。
80Vの電源を短絡した回路は、次のようなものになります。

すると、右端の60Ωは並列となって30Ω、それと真中上の10Ωが直列なので足すと40Ω。この40Ωと、左から2本目の40Ωが並列となるので20Ω、その20Ωと一番左の40Ωが直列になるので60Ω。つまり、60Vの電池から流れ出す電流が1Aという簡単な値になるように、逆算して上手く各部の値が決められている問題なのですね。

したがって、図4のように、10Ωに流れる電流は、左から右に0.5Aであることが分かりました。
つぎに、80Vの電池を生かして60Vの電池を短絡させた回路は次のようになります。

これも、一番左の40Ωが並列で20Ω、真中の10Ωを足して30Ω、この30Ωと右から2本目の60Ωが並列となって合成抵抗値が20Ω、これと一番右の60Ωを足して80Ωとなり、やはり80Vの電源から流れ出る電流が1Aとなるように上手に値が決定されているんです。
これを元にして各部の電流を求めると次のようになります。

図6より、10Ωの抵抗に流れる電流は、右から左に向かって(2/3)アンペアと求めることができました。
以上より、60Vの電源を生かした時は左から右に0.5アンペア、80Vの電源を生かした時は右から左に向かって(2/3)アンペア、これらを重ね合わせた結果、右から左に向かって1/6アンペアの電流が流れる、ということが求められます。設問は「10Ωで消費される電力」を求めていますから、I^2Rの式を用いて、10/36、つまり約0.28Wが答えとなるわけです。
図2の問題も同じ手法で正解が求まりますが、こちらは直感的に「21Vの電池と3Ωの抵抗が直列になっているものに4Ωの抵抗が接続されているので、回路に流れる電流は3アンペア」と求めることができますが、何故それが言えるのか?というのはこの先、テブナンの定理あたりで話をしていきたいと思います。
今回お話した、「線形回路においては重ね合わせの原理が成立する」というのは非常に重要な原理ですので、必ず知っておいていただきたい一件でした。これを知っているだけで、いろいろな国家試験のちょっと難しめな問題が容易に解けるようになるのではないかと思います。先に種明かしをしてしまいますけど、実はコンデンサ回路でもちゃんと成立します。(それを利用した出題が実際に電験3種の試験でありました↓)
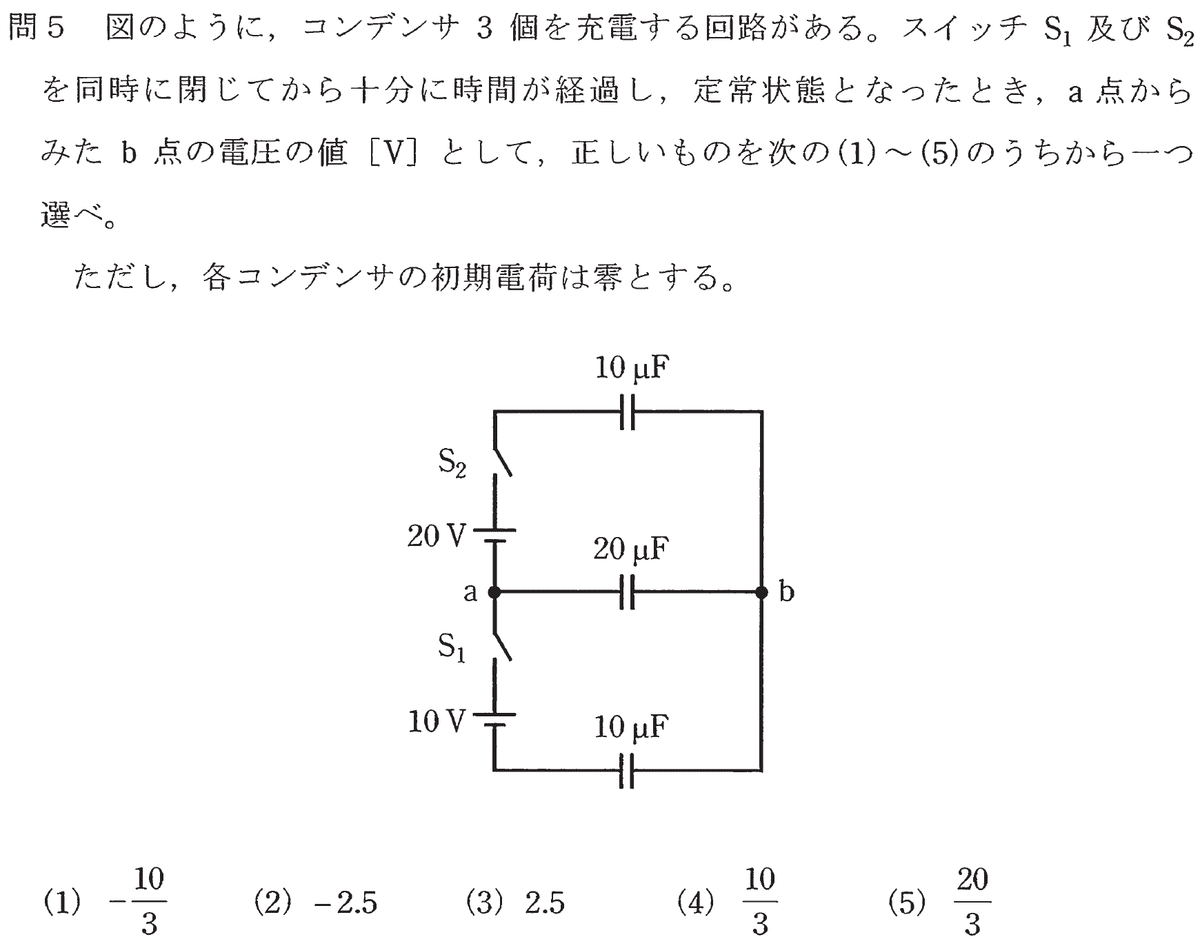
これについては、忘れていなければ、コンデンサの性質の話でまた取り上げることにします。
それではまた。
以上。
