
両立的選言か排反的選言か
本記事には重大な間違いがあります。すみません。訂正情報は、
選言の真偽とはいったい何なのか:(¬A∨B)≡(A→B)に根拠はあるのか|カピ哲!|note
選言の真偽とはいったい何なのか:(¬A∨B)≡(A→B)に根拠はあるのか
http://miya.aki.gs/miya/miya_report38.pdf
・・・をご覧ください。
***************************
※AならばB(A→B)の普遍的真理値が現実世界により根拠づけられるのは、あくまで前件が真の場合のみである|カピ哲!|note
の続きです・・・
****************
先に説明した¬A∨Bは、野矢氏の言われる「両立的選言」(野矢、27ページ)であるが、¬A▽Bというふうに「排反的選言」(野矢、27ページ)とするならば、2等辺三角形の事例と齟齬をきたすことがなくなる。

そして、(¬A▽B)と(A≡B)とは同じ真理値を示す。
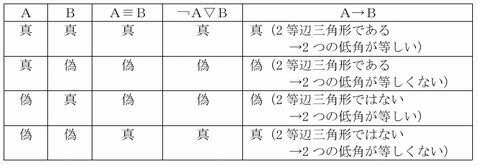
私たちの日常的感覚からすれば、むしろこちらの方が「正しい」ように思える。(¬A▽B)、(A≡B)、さらには(A→B)も同じ真理値ということである。
「または」という言葉の日常的使い方を考えてみれば、「両立的選言」「排反的選言」どちらも間違いではないように思えるが、日本語的には「排反的選言」のニュアンスが強いようにも思える。
どちらを選択しても間違いではないと思うが、その際に条件法の真理値設定、さらには命題論理における公理系や構文論が別のものになっていく可能性はある。排反的選言を採用すれば、少なくともA→(B→A)がトートロジーとは言えなくなることは確かである。
もちろん両立的選言を選択しても、(¬A∨B)≡(A→B)である根拠を現実世界のあり方、あるいは私たちの日常的な言語使用から導き出すことはできないのであるが・・・
野矢氏は「どっちが基本的かなんてことは,たいした問題でもないじゃろう.命題論理では両立的選言は一言で表わせるが,排反的選言はいささか回りくどい表わし方をしなくちゃならん,それだけのことじゃ」(野矢、28ページ)と簡単に済まされているが、実は重大な論点なのである(そして排反的選言は別に回りくどくもない)。
こうなると「トートロジー」とはいったい何なのか、という問題になって来る。
<引用文献>
野矢茂樹著『論理学』(東京大学出版会、1994 年)
