
ドモルガンの法則
これまでの内容については、
電流が流れるか流れないか学(電流学)|カピ哲!|note
をご覧ください。
ドモルガンの法則は以下のとおりである。電流表でも確かに同値となる。
¬(A∧B)≡(¬A∨¬B)
¬(A∨B)≡(¬A∧¬B)
前原『記号論理入門』でも示されているように(前原、107ページ)、ドモルガンの法則を演繹論理で証明しようとすると少々回りくどい過程が必要になる。本章では回路を用いた説明でどこまでシンプルな形にできるのかを試みてみることにする。
まずは¬(A∧B)→(¬A∨¬B)について。これは下の回路図を見ても明らかなように(A∧B)∨(¬A∨¬B)と同値である。
図25 ¬(A∧B)→(¬A∨¬B)は(A∧B)∨(¬A∨¬B)

そして(A∧B)∨(¬A∨¬B)がトートロジーであることを分配律を用いて明らかにすることができる。
図26 (A∧B)∨(¬A∨¬B)はトートロジー

あるいは前章で証明した(A∨B)≡((A∧¬B)∨B)を用いてトートロジーを証明することもできる。
図27 (A∨B)≡((A∧¬B)∨B) を用いた証明

次にその逆、(¬A∨¬B) →¬(A∧B) について見てみよう。下の回路図からも明らかなように、¬(¬A∨¬B) ∨¬(A∧B)でもある。
図28 (¬A∨¬B) →¬(A∧B)は、¬(¬A∨¬B) ∨¬(A∧B)
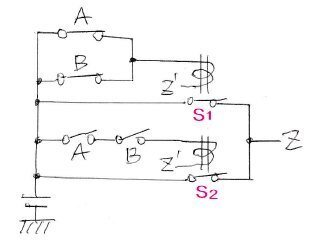
V除去の章で、(A∨B)∧(¬A∧¬B)の回路には電流が流れないことを明らかにした。Aに¬Aを、Bに¬Bを代入すると、
(¬A∨¬B)∧(¬¬A∧¬¬B)つまり
(¬A∨¬B)∧(A∧B)
・・・(¬A∨¬B)∧(A∧B)の回路にも電流は流れない(これもV除去の公理から演繹できる)。∧の意味から(¬A∨¬B)と(A∧B)が同時にonになることがないことは明らかである。つまりS1とS2が同時にoffになることがないのである。このことから上記の回路もトートロジーであることが分かる。
以上より¬(A∧B)→(¬A∨¬B) 、(¬A∨¬B) →¬(A∧B)、つまり¬(A∧B)≡(¬A∨¬B)が証明されたと言えよう。
¬(A∨B)≡(¬A∧¬B)の証明も同様な方法でできる。下の図で示しているように¬(A∨B)→(¬A∧¬B)は(A∨B)∨(¬A∧¬B)と同じ、そして(A∨B)∨(¬A∧¬B)は明らかにトートロジーである。
図29 ¬(A∨B)→(¬A∧¬B)は(A∨B)∨(¬A∧¬B)

(¬A∧¬B)→(¬(A∨B))は、下の図のとおり¬(¬A∧¬B) ∨¬(A∨B)である。
図30 (¬A∧¬B)→(¬(A∨B))は、¬(¬A∧¬B) ∨¬(A∨B)

(¬A∧¬B) ∧(A∨B)は矛盾回路であるから(¬A∧¬B)と(A∨B)が同時にonになることはない。つまり¬(¬A∧¬B)と¬(A∨B)が同時にoffになることがないため、(¬A∧¬B)→(¬(A∨B))の回路全体としては常に電流が流れる(トートロジー回路)ことが明らかとなる。
<補足:相補律を用いた証明>
ここまでの電流学的分析において、以下のトートロジー回路と矛盾回路が示されている。∨と∧の意味を考えれば、以下のように解釈できよう。
トートロジー回路:常に電流が流れる
(A∧B)∨(¬A∨¬B) :(A∧B)と(¬A∨¬B)のどちらかはonになる
(A∨B)∨(¬A∧¬B) :(A∨B)と(¬A∧¬B)のどちらかはonになる
矛盾回路:常に電流が流れない
(A∧B)∧(¬A∨¬B) :(A∧B)と(¬A∨¬B)とが同時にonになることがない
(A∨B)∧(¬A∧¬B) :(A∨B)と(¬A∧¬B)とが同時にonになることがない
・・・どういうことかと言うと、(A∧B)がonのとき(¬A∨¬B)は必ずoffであり、(A∧B)がoffのとき(¬A∨¬B)は必ずonになる。
同じように(A∨B)がonのとき(¬A∧¬B)は必ずoffであり、(A∨B)がoffのとき(¬A∧¬B)は必ずonになる。
それゆえ、¬(A∧B)≡(¬A∨¬B)、¬(A∨B)≡(¬A∧¬B)であると結論づけることができる。
この場合の (A∨B)と(¬A∧¬B)との関係を「相補的」と呼ぶそうである。ブール代数では以下が相補律という公理とされている。(tnomuraのブログ「命題論理のド・モルガンの法則の証明」より。URL: https://tnomura9.exblog.jp/28733058/ )
A∨¬A=1、A∧¬A=0
1は電流学で言えばon、0はoffである。
