
→とはいったい何なのか/トートロジーとはったい何なのか
これまでの内容については、
電流が流れるか流れないか学(電流学)|カピ哲!|note
をご覧ください。
・・・やっとゴールが見えてきた感じです。電流学における証明では常にトートロジーが前提とされているため、健全性や完全性について考察する必要がないこと(しかし不便な面もある)を示した後で、演繹論理の完全性について前原氏の『記号論理入門』の説明をもう少し具体的な形で示して終わりにしようと思います。
これまで何の説明もなしにA→B、B→Aが示せたら直ちにA≡Bが証明できたと結論づけていたが、一応ここで確かめておこう。相補律により証明できる。
A→Bがトートロジー回路
¬A∨B
¬A∨¬(¬B)
¬(A∧¬B)がトートロジー回路
A∧¬Bは矛盾回路=Aと¬Bが同時にonになることはない(1)
B→Aがトートロジー回路
¬B∨A
A∨¬Bがトートロジー回路=Aと¬Bが同時にoffになることはない(2)
(1)(2)より、Aがonのとき¬Bはoff、Aがoffのとき¬Bはon、相補的、つまりA≡Bとなる。
一応証明してみたが、実のところは戸田山氏が説明されているように、→を伴う命題の真理値設定は、A→BだけでなくB→Aが成立して初めて同値となるように意図的に設定されている(戸田山和久『論理学をつくる』名古屋大学出版会、82~83ページ)。野矢氏『論理学』でもP→Qが直ちにP≡Qとならないように真理表3行目(P=偽、Q=真)の真理値を1と意図的に定めたという説明がなされている。野矢氏は「ともかく1か0を入れなければならない」(野矢茂樹『論理学』東京大学出版会、30ページ)としている(※ 野矢氏は「真と偽の代わりに1と0という数値を用い」ている:野矢、20ページ)が、物事の真偽を問うときに、真偽が定められない場所にわざわざ真か偽を加えなければならない義理などどこにもないのである。
要するに、論理学的には図31のような構造(関係)をつくり上げたかったのだ、ということになる。
図31 A→B(AとBは複合命題のことが多い)
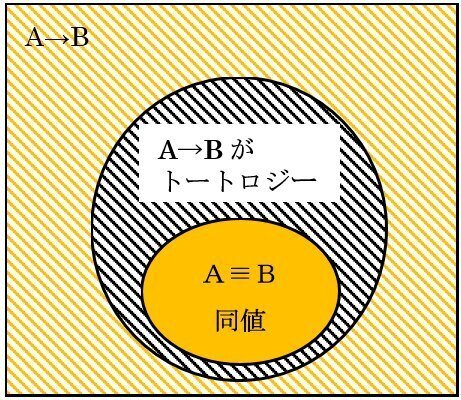
そしてAとBとが→でつなげられるとは、いったいどういう状況なのであろうか?
A→Bは¬A∨Bでもある。¬A∨Bはそもそも真偽を問う命題ではない(コンテクストというか依拠する論理空間によるかもしれないが)。仮に集合論的に考えてみよう。「同値”ならば(→)”トートロジーである」については、それが「正しい」と判断することができる(図31参照)。しかし「同値ではない”または(∨)”トートロジーである」ならばどうだろうか? それは「正しい」「間違い」と判断できる表現ではなく、あくまで図31における斜線の領域(命題のグループ)を指し示しているだけである。「同値である∨トートロジーではない」は図31においてオレンジ色の領域を示すだけである。
これは∧についても同様である。「同値ではない∧トートロジーである」は黒の斜線部分のグループを指し示す。一方「同値である∧トートロジーではない」は指し示す領域が存在しない。しかし特定のグループ・領域を指し示すことができるのかどうかを真偽(正しい・間違い)という判断に転換するためには、さらに別のコンテクスト(「該当する命題が存在すれば真で存在しなければ偽」といったようなもの)を付加する必要がある。
∨や∧を用いた命題論理を直ちに真偽判断と結びつけるのは誤謬となる可能性があるのだ。
このように∨や∧を日常的(別に科学的でも良い)事実認識のコンテクストの中で捉えると→と同列に真偽関係として見做すことができなくなってしまう。ならば(→)とまたは(∨)あるいはかつ(∧)を変換することができなくなってしまうのである。
電流学では、命題論理を単なる回路の形式で示し、真理値ではなく電流が流れるか流れないかを見きわめるだけである。それゆえA→Bと¬A∨Bが同値であることに何の問題もなくなる。それぞれの論理記号を同列に扱うことができるからだ。
ならばA→B(多くの場合AやBは複合命題である)が”証明”されるとはどういうことなのであろうか?
電流学においては
前提と結論を→でつなげるとトートロジー回路になることが示される
・・・それ以上でもそれ以下でもない。そこに別の意味合いはない。電流学において(そもそも論理学においても実際にはそうなのであるが)電流値(真理値)は”設定”されたもの、繰り返すが命題論理とはあくまで”人工言語”なのである。
トートロジーとはその命題が常に正しいことを意味するのではない。そしてトートロジーであることがその命題に何かしらの意味合いを持たせるわけでもない。
電流学的に言えば、常に電流が流れる回路、ということだけ、そして「同値⊂トートロジー」という関係がある、ただそれだけなのである。
