秘密鍵から公開鍵を作る楕円曲線暗号の簡単な仕組み

前回は、秘密鍵とは？公開鍵とは？といってところを紹介してきました。楕円曲線暗号には、署名が使われているという話をしました。

ブロックチェーンの公開鍵から秘密鍵を作成する際に使われる「楕円曲線暗号」について、紹介していきます。

●楕円曲線暗号とは

「楕円曲線暗号」言葉の響きはかっこよくないですか？

ブロックチェーンで使われる「楕円曲線暗号」についてまとめていきます。

●楕円曲線暗号の概要

楕円曲線暗号は、楕円曲線を利用した暗号方式の総称です。

前回説明した署名では、

1、公開鍵から秘密鍵を作り出すため
2、秘密鍵から公開鍵を作り出せないようにするため

を満たすために、楕円曲線暗号が用いられています。

みんなが使える、公開鍵から特定の人が使える秘密鍵作り出せちゃったら、権限奪われ放題になっちゃうので、楕円曲線暗号は大事です。

●暗号の楕円曲線の式とその説明

wikipediaによると、

ある有限体 K 上の式

を満たす全ての点 P=(x,y) の集合に、無限遠点と呼ばれる特別な点 O を加えたものである。x と y は有限体 K の要素。(Kの標数が2または3の場合、上式では不都合が生じるため、標数は2と3以外であるとする。)

が楕円曲線の式です。

グラフのイメージは以下です。不思議な形ですね( ´∀｀)

言葉の補足ですが、

要素っていうのは、

例えば、{1,2,3,4,5,6}という集合があった時の1,2,3,4,5,6が要素です。

有限体Kとは、有限な体のことです。

このままだと、よくわからないので、

まず、「体とは？」というところを紹介して、次に「有限体とは？」

について、紹介していきます。

＊標数については、一旦無視してください。説明すると、命題を用いて説明せざるを得ないことになるので、あとでさらっと説明します。

●体とは？

体とは、一般には

零元を除いて、四則演算が成り立っている集合のこと

と定義されます。

零元というのは、実数でいうなら０のことです。

０含めちゃったら、1/0とか計算できないので、抜きます。

四則演算が成り立つというのは、「足し算」、「引き算」、「掛け算」、「割り算」をした結果、その結果もまた、その集合に属しているということです。

集合というのは、数が集まってできたものです。例えば、自然数、実数、有理数、{1,2,3,4,5,6} などは集合です。

ここでは、具体例として、「体である集合」と「体でない集合」を考えてみます。

●体である集合

最も身近な体の例は、実数です。

実数は数学的には2乗すると０以上の数になるというのが定義ですが、日常生活で使うような、

1、2、1.2、0.333333333333.....、2/5、√２、3.14.......

などやそれにマイナス記号をつけたものを実数と言います。

実数が体である事を確認してみます。

それでは、適当な０以外の二つの実数をとってきてください。（実数では、零元が0なので）

例えば、実数の1/2、1/5、をとってくるとします。すると、

1/2 + 1/5 = 7/10（足し算）

1/2 - 1/5 = 3/10（引き算）

1/2 * 1/5 = 1/10（掛け算）

1/2 ÷ 1/5 = 1/2 * 5 =5/2（割り算）

という感じで、実数を四則演算しても、その結果が実数になっていることが確認できるかと思います。

他の場合についても同様に確かめれます。

実数が体である事が確認できました。

●体でない集合

では、体でないものは、なにがあるでしょうか？

例えば、整数は体ではありません。なぜでしょうか？

例えば、整数の1、-2を考えてみましょう。

1 + (-2) = -1 （足し算）

1 - (-2) = 3 （引き算）

1 * (-2) = -2 （掛け算）

1 ÷ (-2) = -1/2 （割り算）

割り算だけ、-1/2となり、整数でないことがわかります。

だから、体ではありません。

ここで、いや、(-2) ÷ 1 = -2 だったら成り立つじゃん

と思うかもしれませんが、0以外の整数の全ての要素に対して、四則演算が成り立たなければいけません。

だから、整数は体ではありません。

●有限体とは？

集合Kが有限体であるとは、

Kが有限な体であること。つまり、Kの零元（0）を除いた数で四則演算が成り立ち、Kの要素が有限個なこと。

です。

ちなみに、先程、体として紹介した実数も、実数の個数が有限個ではないので、有限体ではありません。

●有限体の一例

ここで、有限体の一例を紹介します。

それは、零元を除いた整数を標数pで割った余りの集合を有限体の一例として、紹介します。(Z/pZ)* と書きます。

標数は、整数を割る素数のことを言います。（厳密には違うのですが、ここでは説明のためにそう定義します。）

例えば、p=7（標数）の時、

7で割った余りは、0、1、2、3、4、5、6となります。

だから、

(Z/7Z)* = {1, 2, 3, 4, 5, 6}　（0は零元だから省く）

と書けます。

これから、(Z/7Z)*が有限体かどうかを確認したいです。(Z/7Z)*が有限であることはわかっています（要素が６個しか無いので）。だから、(Z/7Z)*が体であることを確認します。つまり、(Z/7Z)*の要素を二つ取ってきても、四則演算が成り立ち、その結果が(Z/7Z)*の要素であることを確認します。

ここで、思い出して欲しいのが、(Z/7Z)*は整数を7で割った余りから零元（０）を除いた集合(={1,2,3,4,5,6})であることです。

ここに注意しながら、(Z/7Z)*が体であることを確認していきましょう。

１、足し算

2 + 6 = 8 = 1（8を7で割った時の余りが1なので）

これは、{0,1,2,3,4,5,6}の中に含まれていますね。

他の足し算の組み合わせについても同様に確認していきます。

2、引き算

4 - 6 = -2　の時、

-2はこの場合どんな値になるのでしょうか？

7で割った時の余りと同じになるはずなので、7をいくら足しても値は変わりません。（例えば、2、9(=2＋7)、16(=2+7+7)は、7で割った余りが2で、同じです。）

-2 + 7= 5 となるので、ここでは、

-2 = 5 として扱えます。

確かに-2は{0,1,2,3,4,5,6}の中に含まれていますね。

他も同様に確かめます。

3、掛け算

2 * 4 = 8 = 1（8を7で割った時の余りが1なので)

1は{0,1,2,3,4,5,6}の中に含まれていますね。

他も同様に確かめます。

４、割り算

1 ÷  3 = 1/3　の時、

1/3の値はどうなるのでしょうか？

ここでは、1/3が(Z/pZ)*={1,2,3,4,5,6}の要素であることを確認したいです。

1/3に成り立つ式は、

3 * 1/3 = 1　であるはずです。（割り算の定義から）

こうなるような、1/3を{1, 2, 3, 4, 5, 6}の要素から見つけてきましょう。

3 * 5 = 15 = 1 mod 7（15を7で割ったら余り1なので） 

となります。

なので、1/3 = 5です。

確かに、1/3は、{0,1,2,3,4,5,6}の中に含まれていますね。

他の割り算も同様に確かめます。

これから先は、

このような標数がp(例では7）で割ったような集合(Z/pZ)*（例では、(Z/7Z)*={1,2,3,4,5,6}）

を有限体として、

x,y が(Z/pZ)*の要素であるとして、

こちらの式を考えていきます。

＊ちなみに体は”からだ”ではなく、”たい”と呼びます。

●暗号の楕円曲線の式のイメージ

さて、先程紹介した

がどんなグラフなのかについて考えていきます。

では、

まずは右辺だけとりだして、こちらの３次関数は、このようになります。

ただし、a=-2, b=0 の場合です。

で、y^2があるため、x軸にたいして、グラフが対象になるはずなので、結局、楕円曲線

は下のようなグラフになります。

ただし、a=-2, b=0 の場合です。

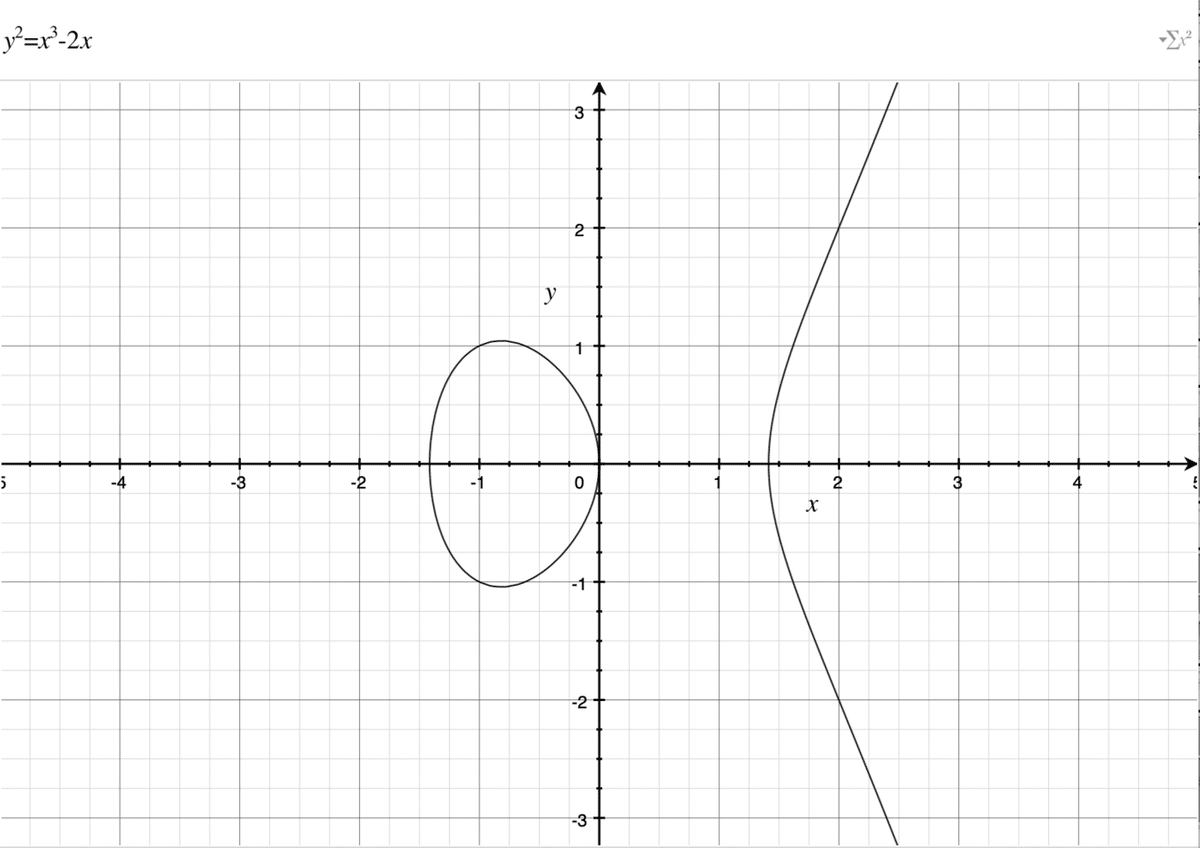
ただし、あくまで、x,yは(Z/pZ)*の要素、つまり、p(標数)で割ったあまりの値（整数）になっているはずなので、曲線ではなくて、点がプロットされている感じにはなります。

●楕円曲線暗号の計算の仕組み

さあここまで、楕円曲線の式だとか、グラフだとか説明してきました。

どんな計算が行われているのでしょうか？

●楕円曲線の加算について（楕円加算）

楕円曲線では、点と点の加算を定義します（楕円加算）。

具体的にどんな加算なのかというと、

1、点Pと点Qを加算する場合、点Pと点Qを結ぶ直線を引き、楕円曲線との好転を求める。
2、その交点とx軸に関して対称な楕円曲線上の点を点Pと点Qの加算と定義する。

といったものです。ざっくり図にすると、

こんな感じです。青丸が点Pと点Qの加算の結果になります。

●楕円曲線上の２倍加算について

先ほどは、2つの異なる点の加算を定義しましたが、今回は同じ点を加算した場合、則ち、２倍加算した場合の計算についてまとめていきます。

点Pの2倍加算の手順は、

1、点Pの接線を引く
2、楕円曲線との交点を求める
3、その交点とx軸に対して、対称な楕円曲線上の点を求める。
4、その点をPの2倍加算である2Pとして定義する。

青丸を点Pとした時、水色丸を点Pの2倍加算である2Pとします。

●楕円曲線暗号の計算の仕組み

で、この楕円加算を使って計算をしていくのですが、どうやって計算していくのでしょうか？

手順としては、

1、p(標数),a,bを決める。基準点Gを決める。
2、点Gと点Gの2倍加算である、点2Gを求める
3、2の行為をn回(秘密鍵の値)繰り返す
4、nGを公開鍵の値として取り出す

です。点Gに対して、先ほど紹介した2倍加算をn回（秘密鍵の値）分繰り返し、nGを公開鍵として取り出します。

nが大きくなればなるほど、nG、Gから、nを求めるのが難しくなります。つまり、公開鍵から秘密鍵を求めるのを困難にしています。

楕円曲線上の離散対数問題というものを利用しています。楕円曲線上の離散対数問題を説明するのは大変なので、離散対数問題を説明すると、

離散対数問題とは、例えば、

3^k = 6 mod 7　（6 mod 7とは,7で割ったときにあまりが6になる値という意味）
を満たすkを求めよ

みたいな問題です。有限体{0,1,2,3,4,5,6}の中であれば、答えは4です。確認してみてください。

これは具体的な解法があるわけではないので、手計算で求めることになります。

これは、k=4で済みましたが、これを巨大な数字にすれば、スパコンでも解くのはしんどくなります。

先ほどのGを３に、nGを6 mod 7、nをk　に置き換えてみれば、を求めるのがしんどくなるのがわかるかと思います。

●まとめ

以上、楕円曲線暗号について、ざっくり紹介してきました。

まとめると、楕円曲線暗号は、公開鍵から秘密鍵を割り出せないようにするための手法です。

そのために、楕円曲線の2倍加算、楕円曲線上の離散対数問題を用いて、秘密鍵を求めるのを難しくしています。

ああ、もっと代数学真面目に勉強しとけば良かった笑